人力资本思想最早起源于18世纪中期, 随着人类进入工业时代, 劳动生产力随着机械与科技的发展发生重大变革. 以亚当·斯密为代表的古典经济学家指出人所具备的能力、知识及经验对国家财富生产的重要作用, 而且教育通过作用于劳动力从而对经济生产、国家财富产生深远影响. "人力资本"的正式概念由Schultz (1961)提出, 以探究当时经济增长快于土地、资本、劳动力增长的原因. Schultz (1961)将人力资本视为劳动力所具备的知识、技术、能力及健康所构成的一种资本, 强调投资对于人力资本的重要性. 随后人力资本理论得到了迅速的发展和应用(Becker (1962), Romer(1986, 1987, 1990), Lucas (1988), Mankiw et al. (1992)). 与此同时, 得益于个体微观数据的发展, 微观层面的人力资本研究也日益增多(Griliches and Mason (1972), Angrist and Keueger (1991), Duflo (1998), Ashenfelter et al. (1999), Dawson (2012)).

尽管与人力资本相关的文献已经相当丰富, 但人力资本研究的基础即人力资本的度量问题依然缺乏系统的梳理和规范. 各类研究采用不同的度量方式和指标, 包括教育、培训、"干中学"、健康或者各种能力等, 但这些指标代表人力资本不同方面的内容. 各种人力资本度量指标反映不同的内涵、形成渠道和作用机制, 因此会直接影响研究结果及相应的政策涵义.

由于个体人力资本包含多方面的内容, 微观的度量指标直接影响宏观度量指标的含义. 另一方面, 从微观个体的人力资本到宏观经济体人力资本总量, 也受到不同技能劳动力加总方式的影响. 当由个体人力资本度量指标加总得到一个国家和地区的宏观人力资本总量时, 个体人力资本内涵差异, 以及多种个体技能加总的方式的差别就直接影响人力资本的作用. 现有研究中关于人力资本对经济增长和发展的作用程度没有定论, 比如有些研究发现人力资本起着主要的作用, 而另外一些研究发现人力资本作用有限, 其中人力资本度量差异是导致该争论的重要原因之一.

针对这一问题, 本文将系统梳理、分析人力资本的度量问题. 本文主要贡献在于, 首先, 通过理论模型将个体人力资本度量与宏观人力资本总量度量及功能直接联系起来, 使得这两个层次的人力资本问题融为一体. 其次, 在包含教育、培训等多种局部人力资本度量指标中, 劳动者个人的工资是个体生产效率的体现, 因此是个体人力资本的综合表现. 本文重点研究以个体工资为度量基础的不同宏观人力资本总量度量的方法, 深入分析其人力资本度量机制. 同时, 我们利用中国数据建立相应的人力资本度量指标, 讨论不同度量方法对人力资本的发展趋势描述的差异, 以及对其作用功能的影响. 本研究从基础概念及理论方法角度为相关人力资本的研究及政策分析提供依据.

本文首先通过理论模型将基于个体的微观人力资本与基于经济体的宏观人力资本连接起来, 系统阐述人力资本度量的理论基础, 从微观到宏观角度深入分析人力资本度量的内涵问题. 其次, 本文深入分析从个体人力资本到宏观总体人力资本的加总计算过程中不同技能劳动力人力资本的相互关系所带来的影响. 然后, 本文具体比较分析了基于个人工资的三种人力资本度量指标, 即传统的效率单元(efficient units)、新兴的广义人力资本(generalized division of labor)、和国际常用的Jorgenson-Fraumeni (J-F)终身收入人力资本这三种不同度量指标. 我们从微观个体与宏观总体两个层面详细讨论了其计算机理, 以及个体生命周期内人力资本的动态变化产生的影响. 最后, 我们利用中国的数据计算了1985到2018年这三种人力资本指标数据, 比较分析不同指标所反映的我国人力资本变化趋势及对我国地区经济发展差异的解释程度.

人力资本价值首先通过劳动力市场来体现. 根据经济学原理, 在完全竞争市场基本前提下, 工资反映了劳动力的边际生产力. 而劳动力的边际生产力取决于物质资本、生产技术及劳动力所具备的人力资本. 在内生经济增长理论发展之前, 传统经济增长理论认为劳动力是同质的, 因此在宏观生产函数中劳动力的工资没有差别, 这一处理显然与经济运行的现实不相符, 造成微观人力资本理论与宏观经济增长模型脱节. 随着内生经济增长理论将人力资本引入经济增长模型, 宏观经济发展与微观劳动力人力资本直接联系起来, 从而个体人力资本状况可以影响整体经济增长.

我们首先建立包含人力资本的宏观经济增长理论模型, 再进一步建立起个体人力资本、劳动力市场及经济增长间的内在联系.

假设一个经济体的总量生产函数为:

(1) $ \begin{equation} Y = F(K, H, A), \end{equation} $

其中$ Y $是社会总产出, $ K $是物质资本量, $ H $为人力资本总量, $ A $为代表技术发展水平的全要素生产率. 在古典经济增长模型中, 人力资本$ H $由劳动力总量来代表, 即将不同技能劳动力简单加总得到总体劳动力, 不同技能劳动力对产出贡献相同.

为了将人力资本引入生产函数并体现劳动力的异质性, 我们需要解决两个问题, 一是如何衡量个体劳动力的人力资本, 二是如何将个体劳动力进行加总以得到生产中使用的总体人力资本量.

按照一般性的处理方式, 我们首先将劳动力根据技能级别分为$ N $级, 技能层级最低的称为基础层级劳动力, 其余则为不同层级技能劳动力. 则人力资本总量可以表示为:

(2) $ \begin{equation} H= \phi(h_{1}, h_{2}, \cdots, h_{N}), \end{equation} $

其中$ \phi $为各技能层次劳动力人力资本的加总函数, 取决于不同技能劳动力间的替代或互补关系. $ h_{i} $为第$ i $级技能劳动力的人力资本, 由该层级劳动力质量$ q_{i} $与数量$ l_{i} $决定:

(3) $ \begin{equation} h_{i}= q_{i}l_{i}, \quad i=1, 2, \cdots, N. \end{equation} $

劳动力质量$ q_{i} $可以视为个体劳动力所具有的人力资本数量, 可由人力资本单元来表示. 一般情况下, 为了简化处理, 可以将基础层级劳动力的人力资本单元数量定义为1, 即$ q_{1}=1 $, 这样人力资本总量就是基于基础层级劳动力的数量.

个体劳动力的人力资本度量与总体人力资本度量之间的连接可从个体劳动力边际生产力出发展开分析. 根据新古典经济学的基本假设, 劳动力工资等于其边际生产效率, 即可得第$ i $级技能劳动力实际工资:

(4) $ \begin{equation} w_{i}=\frac{\partial Y}{\partial l_{i}}=\frac{\partial F}{H}\cdot\frac{\partial \phi}{\partial h_{i}}\cdot q_{i}. \end{equation} $

等式右边第一项为总人力资本的边际生产力, 即单位人力资本的边际增加所带来的额外产出; 第二项$ \frac{\partial \phi}{\partial h_{i}} $为对总体人力资本的边际贡献率, 即第$ i $级技能劳动力人力资本的增加一单位时所带来的人力资本总量增长; $ q_{i} $为第$ i $级技能劳动力的人力资本质量, 即人力资本单元数量.

从方程(1)、(2)和(4)可见, 个体劳动力首先通过其人力资本质量$ q_{i} $影响人力资本总量$ H $, 进而影响产出. 其次, 不同技能劳动力在生产中的相互替代及互补关系也影响人力资本总量, 通过方程(4)第二项的人力资本$ h_{i} $对总人力资本的边际贡献率来体现. 这一边际贡献率取决于不同技能劳动力的相互关系, 会影响其在生产过程中的效率, 从而影响其工资.

所以, 假设生产函数关于$ q $是可分的, 个体劳动力的生产效率, 即其市场工资, 取决于以下方程:

(5) $ \begin{equation} w=f(K, H, A;q)=f_{k}(K, H, A)\cdot q. \end{equation} $

工资首先取决于宏观经济条件, 即物质资本总量、人力资本总量及全要素生产率, 然后取决于个体人力资本量. 因此, 人力资本的度量就包含两个重要方面, 即个体人力资本度量及宏观人力资本度量, 并且两者存在紧密的内在联系. 我们首先讨论个体人力资本度量问题, 然后讨论宏观人力资本度量问题.

在同一个国家或者地区, 其物质资本水平、人力资本总量和技术水平是相同的, 因此, 个体人力资本对工资的影响模型可以简化为:

(6) $ \begin{equation} q=g(s, ex;c, d;o)=g(s, ex;u), \end{equation} $

其中, $ s $为教育程度, $ ex $为"干中学"积累的技能, $ c $是认知能力, $ d $为非认知能力, $ o $为影响个体工资的其他不可观测的能力, $ u $为影响工资的所有不可观测因素. 个体人力资本的质量$ q $可以从两方面进行衡量: 第一部分是可观测的人力资本; 第二部分是不可观测的人力资本, 如认知和非认知能力, 这两种能力既受到先天基因遗传的影响, 也会在后期成长过程中得到不同的发展.第三部分是影响个体人力资本的随机项.

由模型(6)可见, 人力资本的后天积累通过教育及"干中学"的途径实现, 因此教育程度成为度量个体人力资本的传统指标.对于"干中学", 常用度量指标为工作年限.但是由于个人职业差异, 工作内容和所需技能千差万别, 同样的工作年限所带来的人力资本积累差别很大, 不能准确度量个体通过"干中学"获得的人力资本水平.目前最新研究深入到个体工作性质及内容, 以及各种工作任务等(Gibbons and Waldman (2004), Lazear (2009), Autor and Handel (2013), Robinson (2018), Cavounidis and Lang (2020)).但由于数据缺乏, 对于"干中学"积累的人力资本度量也非常有限.基于上述原因, 传统上最常用的个体人力资本度量指标为教育程度指标, 如个人受教育年限与所获学位等.

现有研究将个人能力区分为认知能力和非认知能力(Kuhn et al. (2000), Heckman and Rubinstein (2001), Hanushek and Woessmann (2008), Kautz et al. (2014)), 两种能力既受天生遗传的影响又取决于后天的培养方式(Cobb-Clark et al. (2019))和所处环境等因素.个体认知能力和非认知能力的度量取决于对这些能力的专门测试.目前较为常用的包含能力测试的数据库是PIAAC调查数据(Valiente and Lee (2020)), 但该数据库集中在OECD国家.

因此, 考虑到个体人力资本内涵的复杂性及相应数据的缺乏, 个人工资被直接用于度量人力资本, 因为工资能够全面反映个体人力资本的多个方面, 包括教育、"干中学"、认知能力和非认知能力等.根据公式(5), 个人工资取决于宏观经济条件及个人特征.在同一个经济体宏观经济条件相同的情况下, 工资主要反映个体人力资本的差别.

基于工资度量的人力资本主要有两种方式, 第一种是通过不同技能劳动力的相对工资来区别其个体人力资本差异, 如效率单元, 又称为单位劳动力等价量(Hansen (1993), Jones (2014)).效率单元通过相对工资将不同技能的劳动力转化为不同数量的基础技能层级劳动力.与基于劳动力相对工资的度量方法不同, 另一种常用的人力资本度量方法是基于劳动力个体的绝对工资, 并由此估算个人终身收入来度量个人人力资本.目前国际上广泛使用的主要是Jorgenson-Fraumeni终身收入法(Jorgenson and Fraumeni(1989, 1992a, 1992b)).

除了度量个体人力资本, 在学术研究及相关政策分析中, 度量一个经济体的总体人力资本同样重要. 宏观总体人力资本是个体人力资本的加总, 直接影响一个经济体的发展.

不同的宏观人力资本度量指标所反映的微观个体人力资本内涵存在差异. 传统上一般使用劳动力教育指标, 如平均受教育年限, 来反映宏观经济体的人力资本水平(Barro and Lee(1993, 1996, 2001, 2013)). 但是由于教育仅代表人力资本的一部分, 因此, 本研究不深入探讨以教育为指标的人力资本度量.

为了综合反映人力资本内涵, 宏观人力资本的度量主要是使用劳动者个人的工资. 效率单元是建立在相对工资基础上, 因此, 在同一经济体内, 物质资本、技术进步等宏观经济条件对于个体工资的影响被相互抵消(见公式(5)), 相对工资反映出不同技能劳动力的综合人力资本差异.

从个体人力资本的效率单元来加总形成人力资本总量时面临复杂的加总问题. 由人力资本加总函数(2)可见, 不同的加总方式得到的人力资本总量将不同, 那么人力资本所带来的产出也存在差异, 进一步会影响人力资本对经济增长的贡献程度. 最简单的方法就是将所有劳动力的效率单元直接相加, 如通过相对工资将各层次技能劳动力工作时间投入转化为数量不等的基础层级劳动力单位时间投入量, 然后加总得到总劳动力时间投入(Hansen (1993)). 这种简单相加其实就是线性加总, 暗含了在生产过程中不同技能人力资本为完全替代关系的假设, 而没有考虑不同劳动力之间存在的更为复杂的替代及互补关系.

目前已有大量文献批判技能完全替代弹性的假设(Katz and Murphy (1992), Ciccone and Peri (2005)). 我们将根据广义劳动力分类法(generalized division of labor, 简称为"GDL") (Jones (2014))计算并讨论不同技能人力资本加总的宏观人力资本度量问题.

本章将阐述效率单元与广义人力资本的度量机理, 这两种度量方式均基于工资度量个体人力资本, 但其加总核算方法遵循不同的技能替代假设.

效率单元又称为单位劳动力等价量, 最初由Hansen (1993)构建来度量劳动力工作时间投入总量. 本文遵循Jones (2014)构建的效率单元度量方法, 将技能层次最低的基础劳动力人力资本作为度量单位, 以技能劳动力与基础劳动力的相对工资体现技能劳动力人力资本量, 再通过线性加总获得总体人力资本总量. 其中, 该方法将一个基础劳动力所具有的人力资本量作为度量单位, 称为"效率单元", 然后计算社会中劳动力效率单元总数, 以代表经济体劳动力人力资本的总量. 总体人力资本为各层级人力资本的线性加总:

(7) $ \begin{equation} H=\sum\limits_{i=1}^{N}h_{i}=\sum\limits_{i=1}^{N}q_{i}l_{i}=q_{1}\left\{l_{1}+\sum\limits_{i=2}^{N}\frac{q_{i}}{q_{1}}l_{i}\right\}. \end{equation} $

结合式(4)得到技能劳动力与基础劳动力之间的相对质量差异与相对工资相等:

(8) $ \begin{equation} \frac{q_{i}}{q_{1}}=\frac{w_{i}}{w_{1}}. \end{equation} $

由于基础劳动力技能层级低, 在不考虑不同地区及不同时间基础劳动力质量差异的情况下, 可将$ q_{1} $视为1. 另外, 即使一个经济体在不同时点、或不同经济体的一个效率单元所代表的人力资本量即$ q_{1} $是不同的, 但是基础劳动力质量差异可能不大, 所造成的影响有限, 因此, 一个经济体中的效率单元总量具体计算如下:

(9) $ \begin{equation} H_{U}=\sum\limits_{i=1}^{N}\frac{w_{i}}{w_{1}}l_{i}, \quad i=1, 2, \cdots N, \end{equation} $

其中, $ w_{i} $、$ l_{i} $分别表示第$ i $层次技能劳动力的工资与劳动力数量, $ w_{1} $表示技能层次最低的基础层级劳动力工资, $ N $表示技能层次数.

Jones (2014)在所提出的广义劳动力分类法中改进了上述效率单元线性加总的方法, 即放松了不同技能劳动力完全替代的假设, 大大降低了技能单元的计算局限性. 其方法可以涵盖不同技能劳动力各种替代的可能性, 将在一定技术条件下将不同技能劳动力在经济生产中的相互关系纳入人力资本总量的计算中, 因此称为"广义人力资本". 其具体计算模型如下:

(10) $ \begin{equation} H_{\rm GDL}=\left[h_{1}^{(\theta-1)/\theta}+Z(h_{2}, h_{3}, \cdots, h_{N})^{(\theta-1)/\theta}\right]^{\theta/(\theta-1)}, \end{equation} $

其中, $ h_{i} $为第$ i $技能层次劳动力的人力资本量, $ h_{1} $表示基础层级劳动力人力资本量, $ Z $表示技能劳动力人力资本总量, $ \theta $为$ Z $与$ h_{1} $之间的技能替代弹性. 该度量模型可涵盖不同技能层次劳动力之间的多重替代关系, 其具体函数形式因技能替代关系不同而具有高度灵活性与适用性, 并且不需要确定技能劳动力内部的替代形式. 对该基本模型进行转换可得到具体测算模型:

(11) $ \begin{equation} H_{\rm GDL}=q_{1}l_{1}^{1/(1-\theta)}H_{U}^{{\theta/(\theta-1)}}. \end{equation} $

当同样以效率单元作为度量单位, 可遵循$ q_{1} $为1的假设. 如果考虑基础层级劳动力质量问题, 则需要更复杂的处理方法及更多的数据, 本文暂不考虑.

广义人力资本与效率单元之间的关键差异在于总体人力资本加总核算层面. 式(9)中, 效率单元将不同技能层次劳动力人力资本直接线性加总, 所遵循的是完全技能替代弹性假设, 忽略了不同技能层次劳动力在生产活动中的分工与协作对整体生产力的影响.

在效率单元中, 增加某一技能层次的劳动力所能增加的总体人力资本量不变, 仅受劳动力自身所具备的人力资本影响, 而与其他技能层次劳动力无关, 即某一技能层次劳动力的边际人力资本量为:

(12) $ \begin{equation} \frac{\partial H_{U}}{\partial l_{_{i}}}=\frac{q_{i}}{q_{1}}=\frac{w_{i}}{w_{1}}. \end{equation} $

这意味着效率单元度量中, 某一技能层次劳动力的边际人力资本仅取决于其效率单元等价数量, 即各技能劳动力本身人力资本与基础劳动力人力资本之间的相对量.

然而, 不同技能劳动力完全技能替代的假设与实际相悖(Katz and Murphy (1992), Ciccone and Peri (2005)). 从社会整体角度来看, 劳动力通过相互作用所实现的人力资本内涵性增长量也应纳入总体人力资本量, 社会分工可提升劳动生产力. 因此, 传统的人力资本度量方法仅注重于个体人力资本的度量, 而未对总体人力资本加总计算方式予以足够重视.

式(10)表明广义人力资本允许不同技能层次劳动力之间存在不同的替代、互补关系, 广义人力资本相较效率单元总量大大扩宽了人力资本度量的内涵边界, 可以更为准确地体现生产活动中实际发挥作用的总体人力资本量. 基于式(10)可以得到基础层级劳动力的边际广义人力资本量:

(13) $ \begin{equation} \phi_{1\_{\rm GDL}}=\frac{\partial H_{\rm GDL}}{\partial l_{1}}=\left\{\frac{H_{\rm GDL}}{h_{1}}\right\}^{1/\theta}q_{1}. \end{equation} $

从式(13)可以看出, $ \phi_{1\_{\rm GDL}}>1 $. 不同于式(12), 式(13)表明当在人力资本总量度量中将劳动力相互替代关系纳入考量范畴时, 劳动力的边际人力资本不只取决于自身所具备的人力资本量, 而且受其他技能层次劳动力的人力资本量影响. 具体来说, $ \phi_{1\_{\rm GDL}} $随劳动力技能替代弹性$ \theta $下降而上升.

当假设人力资本总量函数$ H=\phi(h_{2}, h_{3}, \cdots, h_{N}) $为规模报酬不变的一次齐次函数时, 可以得到:

(14) $ \begin{equation} H=\frac{\partial \phi}{\partial h_{1}}q_{1}H_{U}. \end{equation} $

可以看出, 广义人力资本总量$ H $与效率单元总量$ H_{U} $测算值的差异由基础层级劳动力边际人力资本量$ \frac{\partial H_{\rm GDL}}{\partial h_{1}} $及其劳动力质量$ q_{1} $所决定. $ \frac{\partial H_{\rm GDL}}{\partial h_{1}} $可反映出总体人力资本中技能劳动力与基础劳动力之间由于相互作用所产生的影响.

为了构建基于效率单元与广义人力资本的人力资本度量指标, 我们首先以教育程度作为技能划分标准, 合并小学及以下劳动力作为基础层级, 然后将其它技能层级根据初中、高中、大专、大学及以上四个层级来划分. 基于《中国人力资本报告2020》数据构建1985年至2018年各技能层次劳动力数量与工资省级面板数据, 并获得各技能层次劳动力与基础劳动力的相对工资数据. 具体细节可参见李海峥和熊咸芳(2021).

基于上述基础数据, 本文直接测算出1985年至2018年效率单元的全国及省级面板数据. 而广义人力资本测算则另需技能劳动力人力资本总量与基础劳动力人力资本的技能替代弹性. 本文采用了李海峥和熊咸芳(2021)所计算的分阶段动态技能替代弹性值, 1985年至1994年为3.513, 1995年至2001年为3.065, 2002年至2016年为2.549, 其阶段划分是根据我国经济结构变化, 如市场体制建立、加入世界贸易组织等. 该技能替代弹性值表明上述三个阶段中, 当技能劳动力与基础劳动力人力资本相对工资上升1%时, 其相对需求分别下降3.513%、3.065%、2.549%. 这意味着相对需求对于相对工资的敏感性降低, 技能劳动力在我国经济生产中的重要性上升. 按照上述数据及方法, 本文计算了中国基于效率单元及广义人力资本从1985到2018年国家层面度量指标, 计算结果将在本文第五和第六节详细讨论.

效率单元和广义人力资本使用当年相对工资度量个体人力资本水平. 与之不同的是, J-F终身收入法以绝对工资为出发点, 用个体终身收入度量人力资本存量. 虽然三种方法都以工资为基础, 但是度量了不同的微观个体人力资本内涵, 使用了不同的总体人力资本加总核算方式. 本部分将主要讨论J-F终身收入法的基本理论、计算过程、数据及参数情况.

J-F终身收入法由Jorgenson and Fraumeni(1989, 1992a, 1992b)提出, 在国际上广泛使用, 是OECD及世界银行采用的评估各国人力资本状况的计算方法(OECD (2010), World Bank (2011)). 这一方法从资本收益的思想出发, 假定人力资本可以像物质资本一样在市场上租赁, 人力资本收益每年所产生的货币价值可以用来综合度量人力资本. 按照J-F方法体系, 人力资本的货币价值可以通过个人的预期终身收入得到. 我们结合中国数据实际情况, 改进Jorgenson-Fraumeni终身收入法, 构建了国家及省级层面从1985到2018年人力资本J-F综合度量指标, 建立了人力资本数据库, 并据此描述中国人力资本的区域分布及发展动态(Fraumeni and Li (2010), Li et al. (2013), Li et al. (2014), Fraumeni et al. (2019), 李海峥等(2010, 2013, 2014))¹.

¹ J-F人力资本数据来源: 中央财经大学人力资本与劳动经济研究中心官方网站, http://humancapital.cufeedu.cn/rlzbzsxm.htm; 中央财经大学-电子科技大学数据共享服务平台, http://cedcdata.cufe.edu.cn/cedc/metadata/list.html.

根据个人的工资模型(5)和(6), 个体终身收入现值为:

(15) $ \begin{equation} hc(a)=\int^{T}_{a}[f_{k}(t)\cdot q(s, ex(t))\cdot sr(t)\cdot em(t)]\cdot {\rm e}^{-r(t-a)}{\rm d}t, \end{equation} $

其中$ hc{(a)} $表示$ a $岁个体的终身收入现值, $ T $表示其退休年龄, $ f_{k} $表示所有宏观变量对工资的影响, $ q $表示个体工资函数, $ S $表示教育程度, $ ex $表示工作经验, $ sr $为反映个体健康状况的存活率, $ em $表示就业率, $ r $表示折旧率².

² J-F方法中所有年龄终身收入均使用当年宏观变量, 因此不随时间变化. 为了简化模型, 此公式未列出所有宏观经济变量及不可观测因素对个体工资的影响.

按照J-F倒推法的计算思想, 个体终身收入等于其当年收入加上未来收入, 个体未来收入等于当年与他性别、学历相同但是年长一岁个体终身收入贴现值的加总:

(16) $ \begin{equation} hc(a)=w(a)\cdot em(a)+\int_{a+1}^{T}[f_{k}\cdot q(s, ex(t))\cdot sr(t)\cdot em(t)]\cdot {\rm e}^{G(t-a)}\cdot {\rm e}^{-r(t-a)}{\rm d}t, \end{equation} $

其中$ w(a) $表示$ a $岁个体当年收入, $ G $表示实际工资相对上一年的年增长率. 因为$ f_{k} $表示所有宏观变量对当年工资的影响, 而在J-F方法中所有年龄的终身收入都是按照当年的宏观变量计算, 因此$ f_{k} $为常数. J-F使用外生的实际工资增长率$ G $表示技术进步的影响.

因为在计算该个体未来收入时, 年长一岁的个体工资估算都是考虑当年的物质资本、人力资本和技术水平, 因此$ K $、$ H $、$ A $不随时间变化, 只反映当年的状况, 所以在J-F计算体系中使用外生性的宏观平均工资的年增长率$ G $来反映技术进步所带来的劳动力生产效率的提高.

在得到不同群体的终身收入后, 可以计算得到一个国家当年的总劳动力人力资本存量$ H $.

(17) $ \begin{equation} H(L)=\int_{0}^{L}hc\cdot {\rm d}l, \end{equation} $

其中$ L $表示劳动力人口, $ hc $表示劳动力个体人力资本.

由方程(17)可见, J-F方法计算加总得到一个经济体的人力资本总量时采用了简单线性加总的方法, 与效率单元的加总方式根本上一致. 即一个高技能个体的人力资本量可以由两个低技能个体相加得到, 也就是说可以由两个低技能劳动力来完全替代, 忽略了不同技能层次劳动力间的分工合作引起的人力资本内涵性增加. J-F方法还存在其它局限性, 比如在计算个人终身收入时没有详细考虑个人职业生涯的动态变化(如工作内容、工作培训、工作晋升、工作变动等)对其人力资本积累的影响, 只是简单地假定与该个体相同城乡、性别、学历程度的年长一岁个体的终身收入相同. 后续将详细讨论这一问题.

在使用J-F方法计算劳动力人力资本时, 其当年收入是计算未来潜在收入的基础³. 由于中国的数据中没有所有个人当年的工资, 我们采用微观调查数据并结合经典的Mincer模型来估算个人工资, 以弥补收入数据的缺陷. 具体而言, 我们利用国内6个广泛使用的微观数据库, 估算经典Mincer收入方程(18), 得到分城乡、年龄、性别、教育程度的个体当年收入⁴.

³本文中的劳动力定义为男性16$ \sim $60岁, 女性16$ \sim $55岁的非在校生群体.

⁴ "中国城镇住户调查"数据(UHS)、"中国健康和营养调查"数据(CHNS)、"中国住户收入调查"数据(CHIP)、"中国家庭金融调查"数据(CHFS)、"中国家庭追踪调查"数据(CFPS)和"中国劳动力动态调查"数据(CLDS).

(18) $ \begin{equation} {\rm ln}w=\beta_{0}+\beta_{1}s+\beta_{2}ex+\beta_{3}ex^{2}+\varepsilon, \end{equation} $

其中$ ex $为个体的最大工作年限, 未考虑个体在工作期间可能发生的调整, 如因职业变化或在职培训而导致的经验的中断或者能力提升.

再进一步利用倒推法, 计算个体终身收入. 因为本文计算的劳动力人口已完成正规教育, 不包括在校生群体, J-F倒推法终身收入的计算如下:

(19) $ \begin{equation} hc(a, s)=w(a, s)\cdot em(a, s)+sr(a+1, s)\cdot em(a+1, s)\cdot hc(a+1, s). \end{equation} $

该公式可用于计算分城乡、性别的个体终身收入. 对于$ hc(a+1, s) $的估算, 按照J-F倒推的思想, 如果60岁退休, 则其人力资本为零, 加上59岁相应个体的当年收入便得到59岁个体的终生收入. 以此类推得到每个年龄个体终身收入. 由于在计算年长个体的年收入时, 已经考虑了经验的增长对工资的影响, 因此倒推时经验的变化已包含在年龄变化中.

得到不同个体的终身收入后, 我们还需要估算劳动力人口. 利用普抽查年份的人口数据, 使用永续盘存法等估算得到每年分城乡、性别、年龄及教育程度的劳动力数据, 然后减去在校学生得到劳动力人口数据. 具体见《中国人力资本报告2020》. 最后, 根据个体终身收入和劳动力人口加总得到1985–2018年国家层面总劳动力人力资本.

J-F终身收入法的优势是可以将人力资本量货币化, 有利于相关对比和政策分析.但是J-F方法在估算终身收入时采用了相对简化的处理, 因数据限制, 只是假定个体后续年份的终身收入等于与该个体所处城乡区域、性别和学历程度相同的年长一岁的个体的终身收入, 未将其他可变因素考虑在内.

个体劳动力在正规教育完成之后的生命周期内人力资本积累的路径差别较大, 其积累的方式也存在差异, 对个体人力资本水平进行衡量并刻画其一生中工资的动态变化曲线是较为复杂的问题.这些问题涉及人力资本积累的不同途径, 主要包括: 1)工作后的职业培训来强化和拓展工作技能(Dustmann and Schönberg (2009), Haelermans and Borghans (2012)); 2)通过函授、成人教育, 或者专升本等途径提升教育等级(Jepsen et al. (2016), Goodman et al. (2019)); 3)通过"干中学"来提升人力资本, 包括转换工作或者职业等(Munasinghe and Sigman (2004), Coles and Mortensen (2016)).由此可见, 忽视劳动力人力资本的动态发展会对个体劳动力终身收入的估算造成各种误差, 不能全面系统地衡量其真实的人力资本水平.

因此, 本部分将从个体人力资本的动态出发研究生命周期内人力资本积累的状况, 以及对终身收入的影响, 为J-F估算方法的改进提供依据.根据人力资本形成理论, 正规教育进入工作之后的人力资本变化状况, 得到以下人力资本积累函数:

(20) $ \begin{equation} ex=g(js, jt, jc), \end{equation} $

其中, $ js $为代表"干中学"的工作性质及工作内容, $ jt $为在职培训, $ jc $为工作变动, 工作变动目的是为在劳动力市场中找到更好的匹配, 因此也属于人力资本投资的范畴.

因此, 个人的终身收入可写为:

(21) $ \begin{equation} hc(a)=\int_{a}^{T}\left[f_{k}(t)\cdot g(js(t), jt(t), jd(t))\cdot sr(t)\cdot em(t)\right]\cdot {\rm e}^{-r(t-a)}{\rm d}t, \end{equation} $

其中, $ f_{k}{(t)} $为随时间变动的宏观变量的影响.公式(21)的形式与J-F终身收入法的计算公式(李海峥等(2010, 2013, 2014))有相似的地方.

J-F终身收入法主要依赖工资函数的$ ex $在个人生命周期中的人力资本的后教育积累途径来代表人力资本的动态, 但受限于数据, 其主要通过个人的工作年限的增加来表现.如果年长一岁的个人与年轻一岁的本人的人力资本轨迹不同, 如存在继续受教育、在职培训和工作变动等方面的差别, 则年长者的终身收入不能准确反映该劳动力的人力资本, 从而使J-F度量的宏观人力资本总量与微观个体的人力资本状况脱节.

本部分主要分析个人生命周期人力资本积累的变化对J-F方法计算的终身收入的影响.为了更直观的展现两者在计算结果上的差距, 我们只选取劳动者个人是否参加过在职培训来体现工作过程中的人力资本动态变化.研究表明从长期来看, 在职培训可以提高工资, 促进职位的晋升(Regnér (2002), Haelermans and Borghans (2012)).

数据来自中国家庭收入调查项目(CHIP 2002), 因2002年的调查数据中包含在职培训信息⁵.我们将样本限制在法定工作年龄内的工作人群.使用问卷中的问题"到2002年底一共接受脱产职业培训时间(月)", 将回答为0的定义为未接受在职培训, 其余的为接受过在职培训.工资为调查中自报的年收入, 教育程度定义为初中及以下、高中、大专和大学及以上.年龄减去上学年份减去6得到工作经验年限的值.

⁵ CHIP2002数据详见网址: https://www.icpsr.umich.edu/web/ICPSR/studies/21741.

变量描述性统计如表 1所示, 总共有31.3%的劳动者参加过在职培训活动, 其中男性有30.5%的人参加了在职培训, 女性的比例达到32.1%.分教育程度来说, 初中及以下的人有23.5%的参加了在职培训, 高中比例为30.4%, 大专比例为33.6%, 大学的比例最高为38.5%, 说明教育程度越高接受在职培训的概率就越大.样本数据显示平均培训时长为1.09个月, 其中男性的平均培训时间为1.11个月, 女性的为1.07个月.虽然女性的接受培训的比例高于男性, 但是培训时长不如男性长.此外, 教育程度越高则接受培训的时间越长, 例如初中及以下接受培训平均为0.82个月, 但大学及以上为1.49个月.

改进传统Mincer模型加入工作培训变量为:

(22) $ \begin{equation} {\rm ln}w=\beta_{0}+\beta_{1}s+\beta_{2}ex+\beta_{3}ex^{2}+\lambda_{1}jt+v. \end{equation} $

回归结果见表 2.与基础层级初中及以下相比, 高中、大专和大学及以上皆有较高的教育回报率, 男性回报率分别为13.94%、29.5%和47.89%; 女性回报率分别为22.57%、37.56%和59.93%. 工作经验的回报系数男女分别为1.8%和1.3%.参加在职培训给男女工资带来的提升分别是4.44%和7.96%, 存在显著的正向影响.在职培训的影响大约是高中教育带给工资增长效应的1/3, 是每年经验影响的2.47倍(男性)或者6.12倍(女性).由于在职培训的时间相对较短, 因此在职培训对工资提升很大, 对于人力资本提升的效果非常明显.

估计上述回归结果, 我们进一步计算在职培训对终身收入的影响, 并与不包含该变量的J-F计算方法的结果进行对比.假设每个教育层级的毕业生在入职的第一年接受培训, 根据公式(21)首先计算出个体包含在职培训影响的当年年收入, 然后正推出下一年随时间变动的年收入, 一直递推到退休年龄, 最终叠加得到个体的终身收入. J-F方法是倒推思想, 个体终身收入等于其当年收入加上未来收入, 未来收入由当年更年长个体的终身收入现值决定, 即假定该个体未来收入等于当年与他性别、学历相同但是年长一岁个体终身收入贴现值的加总.

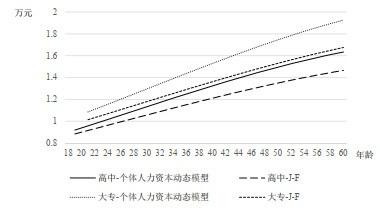
分别计算出两种方法的终身收入之后, 选取相隔10年的两个年龄进行对比, 具体结果见表 3.具体来说, 高中男性通过个体人力资本动态模型计算方法和J-F方法计算出的终身收入在25岁时分别为47.21万元和43.11万元, 前者比后者高了9.51%. 因为个体人力资本动态模型计算方法在进行加总时考虑到了在职培训的带来的人力资本提升, 所以培训后年度工资提高, 从而得出的终身收入大于使用J-F方法计算的结果.另外高中男性在45岁时的终身收入分别为22.75万元和20.59万元, 两者差异是10.49%. 45岁时包含培训的终身收入比J-F计算结果的差异大于25岁时差异, 原因在于在45岁时收入已经高于25岁, 在较高收入的基础上再乘以在职培训的回归系数, 此时得到的年收入比J-F计算的年收入高出的比例更大.因此, 随着年龄的增长, 终身收入的差别是在增加的.

大学及以上男性每个年龄的个体其终身收入大于高中学历的个体, 说明了接受高等教育对人力资本的提升作用.由于同样原因, 在大学学历的更高工资下, 工作培训带来的增加的比例也更大, 因此与J-F计算结果的差距拉大, 例如在25岁时根据人力资本动态模型计算的终身收入比J-F结果高14.67%, 比同一年龄的高中生高出5.16个百分点.对于女性来说, 整体上呈现与男性相同的趋势.男女之间的差异主要表现在女性在各教育程度和各年龄上的终身收入小于男性, 除了受到教育、经验和在职培训系数的影响之外, 女性的退休年龄早于男性, 因此在进行加总时比男性少了5年的收入.

需要注意的是, 我们这里计算终身收入时没有考虑宏观因素的影响, 即没有将技术进步和物质资本的增长考虑进来, 也没有考虑存活率和就业率等问题.这些因素很容易纳入计算过程, 但我们的简化处理可以把重点放在人力资本的动态变化上, 更有利于比较两种方法的差别.

图 1和图 2是分男女对比高中和大专两个教育层级在两种计算方法下的年收入曲线.与J-F方法相比, 不论男性还是女性, 个体人力资本动态模型计算方法得出的结果皆大于J-F方法计算出的年工资水平.此外, 大专学历程度下的终身收入值大于高中学历程度的值.

考虑到了以在职培训为例的人力资本动态变化以后, 计算结果高于只考虑工作年限变动的J-F方法不同.数据表明现实生活中在职培训的比例较高且会提升人力资本.除此之外, 如果考虑到不同职业的"干中学"、在职读学位、工作变化和职业转换等因素, 人力资本积累的变化会受到更多的影响.

上述结果为J-F计算方法的改进提供了依据.根据调查数据, 劳动者平均有31.3%的参加了在职培训, 因此可以用参与培训的比例得到根据人力资本动态模型及J-F模型计算的终身收入的加权平均值, 以调整J-F人力资本总量中因在职培训带来的人力资本增加.

个体人力资本在工作后的动态变化反映了人力资本在生命周期的积累, 因此以终身收入为度量的J-F计算方法可以纳入更深入的微观机制, 以更准确地度量总体人力资本.

J-F人力资本反映的是社会劳动力所具有的人力资本货币价值的总和, 对于个体人力资本度量基于个体终身收入, 度量基础是劳动力年收入. 由于J-F人力资本是基于收入绝对值, 根据理论基础中的式(5), 个体工资不仅取决于其人力资本, 而且受到国家物质资本与技术进步的影响. 一方面, 物质资本与技术进步可影响劳动力生产力, 因此J-F人力资本可反映出这些因素所造成的生产力变化所带来的价值变化量. 另一方面, 由于物质资本与技术进步存在地区差异与动态差异, J-F人力资本的分布模式将与之紧密相关. 然而, 效率单元与广义人力资本的测算所涉及的是相对工资, 一个经济体中不同技能层次劳动力在同一时期所面对的宏观经济条件是一样的, 在计算中被抵消掉, 所以这两种人力资本度量指标一般不受物质资本与技术进步的影响. 但是如果技术进步偏向于增加高技能劳动力的生产效率, 则其影响也会进入以相对工资度量的效率单元及广义人力资本. 这一问题研究需要进一步探索, 我们留待后续研究.

在总体人力资本加总核算层面, J-F人力资本与效率单元一样, 同样是将不同类型劳动力人力资本直接线性加总, 忽略了不同类型个体人力资本在生产中分工合作的影响. 在J-F人力资本度量方法中, 某一类劳动力的边际人力资本为:

(23) $ \begin{equation} \frac{\partial H_{J-F}}{\partial l_{i}}=hc_{i}. \end{equation} $

即某一类型的劳动力边际人力资本仅由其本身人力资本决定, 与其他技能的劳动力无关.

综上所述, 劳动力数量反映的是一个社会中可参与生产活动的总人口, 未反映其人力资本; J-F人力资本计算以劳动力终身收入为依据的人力资本总量的货币价值; 效率单元计算的是总劳动力相当于多少技能层次最低的基础劳动力数; 广义人力资本不仅反映与总劳动力相当的基础劳动力数量, 并且其总数涵盖了不同技能劳动力在生产中通过相互作用实现的人力资本内涵增加量.

由于三种度量方法代表不同的人力资本度量指标, 从不同视角度量了不同的个体人力资本内涵, 宏观上也使用了不同的人力资本加总方式, 因此三种人力资本度量指标所反映的总体人力资本量及其变化趋势也将不同. 我们将对比分析不同度量指标下我国人力资本的发展趋势及动态.

表 4展示了每五年包括劳动力数量在内的各种人力资本指标, 1985年中国劳动力人数为58.14千万, 效率单元总量为59.81千万个基础层级劳动力, 而广义人力资本的结果约为72.90千万个基础层级劳动力. 因为效率单元的度量是基于最低技能的基础劳动力, 包含了劳动力数量与技能劳动力相对效率单元两方面的因素, 其总量应该大于劳动力总量. 但其差别在1985年很小, 效率单元总量比劳动力总量仅高不到3%, 意味着当时各层次技能劳动力与基础劳动力之间的整体技能差异很小, 劳动力人力资本质量普遍偏低. 到了2018年, 效率单元总量比劳动力总量高出49%, 两者之间的差异远远超越1985年的水平. 这一变化说明在1985–2018年期间, 中国人力资本得到巨大发展, 整体劳动力人力资本水平大大上升, 同时劳动力内部技能劳动力与基础劳动力之间的技能差别也不断扩大.

对比效率单元与广义人力资本, 1985年广义人力资本比效率单元高出21.88%, 表明不同技能劳动力之间相互替代、互补带来的人力资本内涵性增加对总体人力资本的影响不可忽视. 到2018年广义劳动力人力资本比效率单元则高出392.87%, 这一巨大的增长说明随着我国技术进步与经济发展, 我国技能替代弹性随着时间推移而逐渐下降, 不同技能劳动力在生产过程中的相互关系对于总体人力资本的作用随之增大, 那么仅按照线性加总方式所计算的总体人力资本会愈加偏离实际. 由于两者均包含劳动力数量与相对效率单元这两个要素, 我们将从个体劳动力边际人力资本角度深化对两者差异变化机制的认识. 广义人力资本在总体人力资本加总中通过技能替代弹性变化反映出个体工资所无法体现的个体劳动力人力资本内涵性增加变化, 效率单元中的个体劳动力人力资本则仅由相对工资所反映的相对效率单元度量, 那么广义人力资本中的个体劳动力边际人力资本的动态变化差异包含了人力资本内涵性增加量的动态变化差异, 因此远大于仅反映相对效率单元动态变化差异的效率单元边际人力资本.

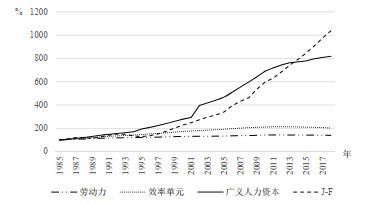
由于J-F人力资本基于终身收入, 与效率单元和广义劳动力人力资本不具直接可比性, 我们将针对这些度量指标的动态趋势展开比较. 图 3展示了不同人力资本度量指标在1985至2018年间的累积增长情况. 在此期间, 劳动力总量增长39.73%, 效率单元总量增长102.39%, 而广义人力资本总量增加了718.42%, J-F人力资本总量增长了937.67%. 整体看来, 劳动力总量与效率单元总量增长缓慢, 近些年甚至开始出现下降趋势. 劳动力总量下降主要由于曾经的计划生育政策造成的人口减少、人口老龄化等, 劳动力总量的下降也带来了效率单元总量的下降. 广义人力资本由于其计算方法的相对合理性呈现出高速增长, 但近年增长势头明显回落, 趋于平稳. 主要是因为劳动力人数减少, 中国的技术进步也日趋平稳, 另外技能劳动力相对工资由于劳动力技能供给结构变化也出现下降.

J-F人力资本总量的增长速度最快, 超过了广义人力资本. 原因之一在于J-F人力资本所基于的终身收入包含了物质资本与技术进步, 也就是说, 从1985到2018期间的物质资本投入加大、技术进步所带来的劳动力生产效率的提高均被计算成人力资本的提升. 另一方面, 技术进步除了提高生产率来增加基于工资的人力资本度量外, 也通过改进不同技能劳动力在生产中的关系来增加人力资本. 通过比较广义人力资本总量与J-F人力资本总量的增长趋势可以看出, 随经济的发展, 技术进步对工资的增长效益高于对广义人力资本总量的增长效益.

表 5展示了中国经济不同发展阶段的相应人力资本增长. 1985–1994年, 广义人力资本年均增长率最高, 约为6.12%; 其次是效率单元, 每年约增长4.03%; J-F人力资本的增长率仅为3.63%, 只略高于劳动力的增长. 在1995–2009这两个阶段, 广义人力资本及J-F人力资本快速增长, 远远超过劳动力数量及效率单元总量的增长速度, 说明这一阶段中国出现快速技术进步, 大大提升了边际劳动生产效率, 不断改进不同技能劳动力随着技术变化的替代及互补关系. 与之相反, 这阶段劳动力数量增加速度迅速减小, 效率单元总量也同样变化.

到了2010至2018年这一阶段, 劳动力数量及效率单元总量呈现负增长, 而广义人力资本维持在2.75%的低增长率水平, J-F人力资本仍然保持7.61%的高增长速度, 说明中国经济逐渐进入相对成熟稳定的阶段, 劳动力人口的负增长的影响开始在各个人力资本度量指标中体现. 同时, 不同技能劳动力之间分工合作导致的人力资本增长速度放缓, 而技术进步带来的劳动力效率仍然维持在高增长率水平.

表 6报告了每五年的各种劳动力人均人力资本指标. 1985年劳均效率单元为0.98, 该劳均量低于1的主要原因是当年技能劳动力年龄分布相对最低技能层级而言偏低, 造成相对工资存在低于1的情况, 且技能劳动力比重也偏低. 而劳均广义人力资本量为1.19, 即劳动力的平均技能水平相当于1.19个基础技能劳动力, 为效率单元劳均量的1.21倍. 到了2018年, 对于劳均效率单元, 劳动力的平均技能相当于1.42个基础劳动力; 但如果考虑劳动力在相应技术条件下的相互替代及互补, 则一个平均技能的劳动力相当于7.00个基础劳动力, 为当年效率单元劳均量的4.93倍. 这说明生产技术的发展使得不同技能劳动力的相互配合促进相应的个体生产效率, 特别是高技能劳动力的生产效率, 进一步拉大了他们与基础劳动力的人力资本差距.

人均J-F人力资本量反映出个体劳动力以货币度量的人力资本值. 1985年, 人均劳动力人力资本为30.79千元, 而2018年升为228.43千元. 作为比较, 1985年按可比价值计算的人均GDP值为0.87千元, 2018年为13.29千元. 1985年人均GDP与人均劳动力人力资本的比率为0.03, 2018年该比率为0.06, 此期间内, 该比率呈上升趋势但是增长减缓, 说明人力资本的生产效率越来越高, 但是增速有所放缓.

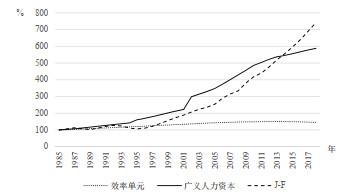
图 4展示了不同人力资本度量指标劳均量在1985至2018年间的累积增长情况, J-F人力资本从1995年起持续高速增长, 劳均广义人力资本在经过快速增长之后从2011年开始放缓. 人均效率单元一直低速变化, 近几年开始出现下降. 表 5展示了不同经济发展阶段劳均人力资本变化趋势, 与总劳动力人力资本的发展趋势基本一致. 仅从劳动力数量来看, 其已经开始下降, 因此被认为是中国人口红利开始消失的依据, 并且人均效率单元的发展趋势也支持这一结论. 但是, 如果考虑相对更准确的度量指标人均广义人力资本或者考虑基于不同内容的人均J-F人力资本量, 则中国劳动力的人均人力资本及总体人力资本都继续增长, 而且增长的速度远高于劳动力及效率单元下降的速度. 因此, 从人力资本角度看, 人口红利可能还能持续.

由于所体现的人力资本内涵要素与度量角度差异, 上述三种基于工资度量的人力资本指标表现出全国总体人力资本量及其变化趋势的不同. 效率单元的分布反映出劳动力数量及技能结构的差异, 而广义人力资本进一步反映不同技能劳动力在生产过程中的相互作用关系所造成的差异. J-F人力资本所度量的总体人力资本中包括物质资本、技术进步这两个与经济发展水平高度相关的因素. 因此, 本部分将在基于上述不同人力资本指标的发展趋势及动态分析的基础上, 进一步考察三类度量指标所表现的人力资本对中国经济发展水平差异的解释程度的差异.

本文主要采用发展核算方法, 这一方法的优势是避免了回归分析中的内生性问题. 发展核算研究方法主要包括两地区要素核算法、协方差-方差法、五地区要素核算法(Klenow and Rodríquez-Clare (1997), Caselli (2005), Hanushek et al. (2017)). 协方差-方差法针对的是整体收入水平差异中的人力资本贡献, 五地区要素核算法则是关于收入水平最高的五个地区与最低的五个地区之间平均收入水平差异, 这两种方法易受极端值影响. 为了避免这个问题, 本文采用两地区要素核算法. 该方法最初核算的是包括物质资本在内的整体要素投入的解释率, 而本文将直接核算人力资本差距对不同收入分位数上的两省份间人均收入差距的解释率(Campbell and Üngör (2020)).

为了研究方便, 将总量生产函数设定为具体的Cobb-Douglas形式:

(24) $ \begin{equation} Y=K^{\alpha}{\rm AH}^{1-\alpha}. \end{equation} $

进而将其转换为如下人均变量的形式以分解出人力资本的贡献:

(25) $ \begin{equation} y=\left\{\frac{k}{y}\right\}^{\frac{\alpha}{1-\alpha}}{\rm Ah}, \end{equation} $

其中, $ y $、$ k $、$ h $分别为劳均产出、劳均物质资本、劳均人力资本, $ \alpha $是物质资本产出弹性. 由模型可见, 人均产出取决于产出的固定资本密度$ (k/y) $, 劳动力人均人力资本密度及其全要素生产率. 本文将具体针对劳动力人均GDP位于90%与10%分位数的省份, 计算人力资本差距占其劳均收入水平差异的比重, 即人力资本的要素解释率(Campbell and Üngör (2020)). 其核算模型如下:

(26) $ \begin{equation} \eta=\frac{h^{90}/h^{10}}{y^{90}/y^{10}}. \end{equation} $

不同年份人均收入90%与10%分位数所对应的具体省份组合不同. 劳动力人均GDP位于90%分位数上的省份位于东部或东北部地区, 比如1985年为辽宁, 2018年为天津. 而劳动力人均GDP位于10%分位数上的省份则均处于西部地区, 1985年、2018年分别为云南、贵州.

表 7依次报告了四个时间段中基于广义人力资本、效应单元、J-F人力资本所得到的平均人力资本要素解释率. 整体而言, 基于广义人力资本的人力资本要素解释率计算结果高于效率单元, 而在2010年前低于J-F人力资本. 例如, 2010年至2018年间, 其人力资本要素解释率分别为0.73、0.36、0.63, 即在此期间, 对90%与10%收入分位数上的省份间的收入差距, 基于上述三种人力资本度量方式所反映的这两个地区的人力资本差距分别占其相应劳动力人均GDP差距的73%、36%、63%. 尽管这些数据并不能完全代表因果关系, 但仍然说明人力资本所占经济发展差距的程度. 如果以相对简单的效率单元来度量人力资本, 会给人以人力资本相对并不重要的感觉. 但如果以更准确的广义人力资本来看, 人力资本的重要性会大大增加, 在相对经济差异中占据重要部分. 这些结论会直接影响相关地区发展政策的制定.

不同人力资本指标所反映的人力资本差距存在明显差异. 以2018年为例, 天津与贵州之间的劳均收入比值为2.7, 其劳均效率单元比值仅为1.04, 广义人力资本与J-F人力资本反映的劳均人力资本差距相对较大, 相应比值均为2.3倍. 这主要是因为广义人力资本是在效率单元的基础上包含了不同技能层次劳动力相互作用所实现的人力资本内涵增加量差异, 更准确地反映了经济生产中的人力资本总量. 而J-F人力资本由于包含了物质资本与技术进步的影响, 并不完全是人力资本的差异. 因此, 基于J-F度量的人力资本由于其内涵不同, 其对经济发展的相对重要程度与效率单元及广义人力资本不能直接相比.

此外, 平均广义人力资本要素解释率的变化趋势与效率单元、J-F人力资本存在不同, 其整体变化幅度相对更高. 具体来说, 平均广义人力资本要素解释率在前三阶段呈倒$ U $形, 总体差异较小, 在0.4$ \sim $0.5之间, 而第四阶段2010–2018年间出现明显上升. 而效率单元与J-F人力资本在前三阶段呈逐渐下降趋势, 在第四阶段虽同样出现回升, 但与第一阶段的差异并不明显. 从整体趋势来看, 基于效率单元的人力资本要素解释率比较低但相对稳定, 而广义人力资本要素解释率呈现超越J-F人力资本的趋势.

通过上述分析, 我们发现广义人力资本可更为准确地体现人力资本对于我国地区经济发展的贡献程度, 而J-F人力资本的贡献率虽然较高, 但包含了物质资本与技术进步因素.

本文从总量生产函数出发, 按照内生经济增长模型引入人力资本, 然后基于个体劳动力工资, 建立了由个体到总体层面相联接的人力资本度量理论模型. 该模型旨在将微观个体人力资本的形成与宏观经济体的人力资本度量及功能直接联系起来, 从而使得宏观人力资本度量指标建立在微观人力资本理论的基础之上.

本文依据人力资本的内涵, 以工资作为个体人力资本的度量指标进行研究, 因为工资反映个人的劳动效率, 包含个人的教育、工作经历、培训及能力等多方面人力资本内容. 在此基础上, 分析基于不同技能劳动力相对工资, 或者基于个人终身收入的人力资本度量方法的内在机理, 并重点讨论了从个体人力资本到一个经济体的总体人力资本的加总问题. 不同技能劳动力由于特定技术条件形成的相互替代及互补关系影响人力资本加总和人力资本总量, 从而影响其对经济发展的贡献程度.

我们对传统的效率单元、新兴的广义人力资本、和国际常用的J-F人力资本度量模型进行深入比较分析. 效率单元主要体现劳动力数量与不同技能层次劳动力的相对质量, 但以不同技能完全替代性为基础进行加总. 广义人力资本在此基础上通过对加总过程的改进来反映不同技能劳动力相互作用而实现的人力资本总量增加. 而J-F人力资本中的个体人力资本是以终身收入来度量, 因此这一总体人力资本直接包含了物质资本与技术进步因素的影响, 同时J-F计算过程也存在加总过程中的完全替代性假设. 另外, 我们实证研究表明现行的J-F计算方法可以通过纳入个体人力资本在生命周期的动态变化来提高度量准确度.

我们利用数据计算了我国从1985到2018年的年度人力资本指标, 即中国效率单元总量, 中国广义人力资本, 和中国J-F人力资本指标. 根据其发展趋势及动态, 这三种人力资本度量指标所反映的人力资本存在明显不同. 整体看来, 1985到2018年间, 我国劳动力总数增长呈下降趋势, 且已开始出现绝对量下降, 基于效率单元总数的人力资本表现出同样的变化趋势; 但是广义人力资本及J-F人力资本却仍然保持持续增长. 人力资本的不同度量所描述的变化动态差异很大, 会直接影响对人力资本分布状况的分析和评估.

我们进一步采用发展核算方法计算不同人力资本指标对中国经济发展的解释程度, 结果显示这些人力资本度量指标对中国经济发展差异的解释程度也存在明显差异. 从对经济发展水平差异的要素解释率来看, 基于效率单元的人力资本解释率最低(低于36%), 广义人力资本相对较高(高于44%), J-F人力资本处于最高的水平(高于51%). 但近年来随着中国经济进入成熟发展阶段, 广义人力资本要素解释率呈现超越J-F人力资本的趋势.

本文结果表明, 人力资本的度量方法直接影响人力资本的相关研究, 影响对人力资本的分布和发展趋势的描述, 对其作用程度的估算, 以及对与之相关的政策分析. 因此, 在人力资本的研究中, 需要认真分析人力资本度量指标的内涵、机理及加总方式, 以便科学地识别人力资本的作用, 为相关人力资本政策提供科学依据.