中国科学院数学与系统科学研究院期刊网

计量经济学报, 2023, 3(1): 1-29 DOI: 10.12012/CJoE2022-0092

论文

基于分组数据测算不均等与贫困等收入分配指标: 兼顾数据截断问题的方法论评估

万广华,1, 江葳蕤,1, 胡晓珊,2

1. 复旦大学世界经济研究所, 上海 200433

2. 上海电机学院商学院, 上海 201306

Measuring Income Distribution Indicators such as Inequality and Poverty based on Grouped Data: A Methodological Assessment Considering Data Truncation

WAN Guanghua,1, JIANG Weirui,1, HU Xiaoshan,2

1. Institute of World Economy, Fudan University, Shanghai 200433, China

2. School of Business, Shanghai DianJi University, Shanghai 201306, China

通讯作者: 胡晓珊, 上海电机学院商学院讲师, 研究方向: 发展经济学、世界经济, E-mail:coralhu_cn@163.com

收稿日期: 2022-10-14  

基金资助: 国家自然科学基金重点项目.  71833003

Received: 2022-10-14  

Fund supported: Naional Natural Science Foundation of China.  71833003

作者简介 About authors

万广华,复旦大学世界经济研究所教授,研究方向:发展经济学、世界经济,E-mail:guanghuawan@yahoo.com

江葳蕤,博士研究生,研究方向:发展经济学、世界经济,E-mail:21110680027@m.fudan.edu.cn

摘要

收入不均等、贫困和中等收入群体占比等指标广受决策界、社会、学术界, 乃至媒体的关注, 也是众多经济社会变量(如增长、消费、投资、教育、健康和犯罪等等)的重要决定因素之一, 但鲜有文献将其纳入到实证模型里, 原因往往在于相关指标或数据的缺失.此外, 家户调查数据顶端和底端的观察值也常常缺失, 给实证估算带来偏差.本文基于2018年的中国家庭追踪调查(CFPS)数据, 评估了由Shorrocks and Wan (2009)提出的基于分组数据“还原”个体观察值, 进而估算不均等和贫困等指标的方法, 并引入条件分布对Shorrocks and Wan (2009)的方法进行拓展, 以便考虑收入分布顶端和底端的数据缺失问题.结果显示, 假设变量服从Dagum分布, 而非Shorrocks and Wan (2009)所使用的对数正态分布, 可以使“还原”偏差保持在可接受的范围内.此外, 本文对Shorrocks and Wan (2009)的方法的拓展, 能够明显降低数据截断所导致的“还原”偏差, 而且在该方法下Dagum分布依然占优.本文的发现表明, 后续研究可在Dagum分布的假设下, 对各省统计年鉴中提供的收入分组数据进行“还原”, 然后测算各省的收入不均等、贫困和中等收入群体占比等等指标, 并据此展开经济学分析, 至少应该将相关指标纳入到实证研究中, 以减少相关指标和模型估算偏误.

关键词： 不均等 ; 贫困 ; 收入分布 ; 分组数据 ; 条件分布

Abstract

Indicators such as income inequality, poverty and the share of middleincome groups are widely concerned by policy makers, society, academia and even the media, and are also important determinants of many economic and social factors (e.g. growth, consumption, investment, education, health, crime, etc.). However, rarely literature included them in empirical models, mainly due to data deficiency. Furthermore, observations at the top and bottom of household survey data are often missing, causing bias in the empirical estimates. Using data from 2018 China Family Panel Studies (CFPS), this paper evaluates the method proposed by Shorrocks and Wan (2009) for "ungrouping" individual observations based on grouped data to estimate indicators of inequality and poverty, then introduces conditional distributions to this method considering the missing data at the top and bottom of the income distribution. The results show that "ungrouping" bias will keep within an acceptable range if assume variables follow Dagum distribution, rather than the lognormal distribution used by Shorrocks and Wan (2009). In addition, this improvement to Shorrocks and Wan's (2009) method significantly reduces the "ungrouping" bias caused by data truncation, and the Dagum distribution still prevails under this method. It is suggested that subsequent research can "ungrouping" the income grouped data from provincial statistical yearbooks under the assumption of the Dagum distribution, and then measure the indicators of income inequality, poverty and middle-income share, etc. before conducting economic analyses. At least relevant indicators should be considered in the empirical study in order to reduce the bias of the relevant models.

Keywords： inequality ; poverty ; income distribution ; grouped data ; conditional distribution

PDF (933KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

万广华, 江葳蕤, 胡晓珊. 基于分组数据测算不均等与贫困等收入分配指标: 兼顾数据截断问题的方法论评估. 计量经济学报[J], 2023, 3(1): 1-29 DOI:10.12012/CJoE2022-0092

WAN Guanghua, JIANG Weirui, HU Xiaoshan. Measuring Income Distribution Indicators such as Inequality and Poverty based on Grouped Data: A Methodological Assessment Considering Data Truncation. China Journal of Econometrics[J], 2023, 3(1): 1-29 DOI:10.12012/CJoE2022-0092

1 引言

贫困和收入不均等以及其他与收入分配相关的议题长期受到国内外政府、社会和学术界的广泛关注. 在国际上, 减贫和缩小贫富差距是由193个国家元首签署、联合国发起和推进的可持续发展目标(SGDs)的核心. 在亚洲, 众多国家包括印度和印度尼西亚等都把反贫困和包容性增长作为重大战略部署. 中国政府更是先后提出了和谐社会、精准扶贫、共同富裕等理念并付诸实践, 创造了人类发展史上的减贫神话(汪晨等(2020)).

显而易见, 不均等和贫困等指标的度量极为重要, 否则将无法监测贫困或收入差距的趋势, 难以科学地制定相关政策, 更不可能开展与收入分配相关(包括政策评估)的研究. 所以, 世界银行建立了知名的Povcal网站, 专门提供国家层面的贫困估算值1; 联合国发展经济学研究院不断更新世界各国的收入不均等指标2; 世界财富与收入数据库(WID.world)也在持续公布国家内与国家间收入与财富分布历史变化数据3. 这些宝贵的数据被大量运用于不同的场合和研究中. 但是, 现有数据库基本上只能提供国家层面的时间序列, 次国家(sub-national)层面的相关指标往往缺失. 这就是为什么在实证模型中直接加入贫困或不均等变量的学术成果相对较少(跨国回归除外). 特别地, 贫困和收入不均等问题在中国的重要性不言而喻, 但鲜有文献在模型中聚焦或控制这些变量, 尽管它们影响诸多经济社会变量, 如增长、消费、投资、教育、健康和犯罪等等.

1https://povertydata.worldbank.org/poverty/home/

2https://www.wider.unu.edu/database/world-income-inequality-database-wiid.

3https://wid.world/data/.

面对与收入分配相关的指标的缺失, 大部分研究都选择直接放弃使用相关变量, 另有部分研究则尝试使用城乡收入差距作为总体收入差距的代理变量(陆铭等(2005), 陈春良和易君健(2009)). 然而, 任何一个国家或地区的收入差距都包括三大成分: 城乡收入差距、城市内部收入差距和农村内部收入差距, 因此使用城乡收入差距作为代理变量会带来一定的误差. 当然, 随着微观调查数据如中国家庭追踪调查(CFPS)/中国综合社会调查(CGSS)/中国家庭金融调查(CHFS)等的出现, 学者们可以估算省级层面的贫困和不均等指标. 但这些微观数据库涵盖的年份有限, 部分样本的代表性也受到质疑.

幸运的是, 早在1970年代, 经济学界就提出了基于分组数据还原个体观察值的方法(如Gastwirth (1972), Kakwani and Podder (1973)), 而且我国国家和部分省市统计局在其统计年鉴上常常公布收入分组数据. Shorrocks and Wan (2009)在前人研究的基础上提出了迭代法, 使得还原的数据更为准确. 但是, 现有的方法均未考虑数据截断的问题. 此外, 将分组数据还原为个体观察值都需要假设具体的统计分布函数. 为此, Shorrocks and Wan (2009)进行了有限的蒙特卡罗实验, 试图评估不同假设的可靠性. 然而, 他们只考虑了三种不同的分布函数, 忽略了其他可能更为可靠的、用以刻画收入分布的函数(如Singh and Maddala (1976), Dagum (1977), McDonald and Xu (1995)).

特别重要的是, 国内外微观调查数据都面临相关变量分布底端和顶端观察值缺失, 尤其是高收入家户抽样不足的问题(王小鲁(2007)), 导致相关研究的可靠性被削弱. 举例来说, 低收入群体数据的缺失将导致贫困率的低估, 高收入群体数据的缺失将导致不均等的低估. 鉴于此, 中国家庭金融调查(CHFS)适当增加了富裕地区和富裕家庭的抽样比重, 但针对CHFS的可靠性仍然存在争议4. 此外, 也有学者尝试使用税务数据(Piketty (2003))或富豪榜数据进行弥补(李实和罗楚亮(2011), 罗楚亮(2019)). 但这些数据与微观调查数据之间缺乏一致性.

4出自甘犁2013年《以公开科学的抽样调查揭示真实的中国》, 是基于李实和岳希明质疑CHFS而发表的《我们更应该相信谁的基尼系数》的回应. 甘文链接: http://www.ciidbnu.org/news/201302/20130223120202706.html. 李和岳文链接: http://www.ciidbnu.org/news/201301/20130123092800706.html.

基于2018年CFPS数据进行蒙特卡罗实验, 本文旨在评估并改进Shorrocks and Wan (2009)提出的基于分组数据的还原方法. 具体而言, 本文首先在Shorrocks and Wan (2009)的基础上考虑了更多的分布函数形式, 评估比较了八种常用的收入分布函数所"还原"的数据的精确度和可靠性. 结果发现, Dagum分布在大多数情况下都有较好的表现. 本文同时评估了Shorrocks and Wan (2009)的迭代调整法的实际效果, 发现该方法在不同状况下都有助于提高"还原"数据的可靠性. 接着, 本文首次引入条件分布法来解决分组数据截断问题, 将无条件分布扩展为双边截断的条件分布来对数据进行"还原", 并评估了其效果. 结果同样表明, Dagum分布能够有效处理顶端和底端收入数据缺失问题.

本文的发现表明, 学术界可以结合使用本文提出的条件分布法和Shorrocks and Wan (2009)的数据还原法, 基于Dagum分布对分组数据进行还原, 从而计算国家或次国家层面的收入不均等、贫困和中等收入群体占比等等指标. 特别需要说明的是, 本文为中国省际贫困与不均等指标的测算提供了重要的方法支持, 这一贡献与张军等(2004)以及郑世林和杨梦俊(2020)类似, 前者将永续盘存法应用于中国早期资本存量的测算, 后者估算了中国无形资本存量.

论文余下的内容安排如下: 第二部分梳理与分组数据处理及数据缺失问题相关的文献; 第三部分讨论分组数据"还原"问题, 并基于蒙特卡罗实验评估八种常见的收入分布函数的还原效果; 第四部分提出条件分布法, 以"还原"两端缺失的数据, 并评估各分布函数的表现; 第五部分结合使用条件分布法和Shorrocks and Wan (2009)的框架, 估算中国历年的基尼系数和中等收入群体占比指标; 第六部分为小结.

2 文献回顾

2.1 收入分组数据的应用

早在20世纪70年代, 基于分组数据测算收入分配指标的研究就开始大量出现(如Gastwirth (1972), Kakwani and Podder (1973), Kakwani (1976)), 相关收入分布函数的设定也随之得到关注(Singh and Maddala (1976), Dagum (1977), McDonald and Xu (1995)). 这些较早的研究大多在参数拟合之后直接生成模拟样本, 而不对还原数据进行调整. Shorrocks and Wan (2009)提出了迭代法, 即根据各组的均值对模拟样本进行迭代法调整, 降低了还原数据与真实数据之间的偏差.

国内也有学者基于收入分组数据, 估算中国的收入分配指标. 如胡志军等(2011)在对数正态分布、威布尔分布和广义贝塔II型(GB2)分布的假设下, 对中国农村和城市居民的收入分组数据进行拟合并据此计算基尼系数. 基于极大似然估计值和各收入区间的人口份额拟合值与样本值的偏差, 胡志军等(2011)发现GB2表现较好, 该发现得到张萌旭等(2013)的证实. 陈建东等(2013)比较了不同分布函数的拟合效果, 发现对数逻辑斯蒂分布占优. 遗憾的是, 现有文献大多没有考虑Shorrocks and Wan (2009)的迭代法, 也没有关注基尼系数之外的其他收入分配指标(祁磊和艾小青(2021)), 更没有考虑数据缺失或截断问题(见下一小节).

2.2 数据缺失问题

影响微观调查数据质量的主要因素有两个: 一是样本代表性; 二是调查个体回复率. 在现实中, 通常会有一定比例的个体拒绝参与调查或者不在家, 导致回复率不足. 该问题又与收入水平相关: 高收入群体所占比例低, 其居住环境更具封闭性, 不容易被抽取; 即便被抽中, 出于隐私或安全考虑, 他们有动机隐瞒真实收入水平或者直接拒绝接受调查(no-response) (Korinek et al.(2006, 2007), Sabelhaus et al. (2012), Burkhauser et al. (2011)). Deaton (2005)发现通过家户调查得出的人均消费远低于国家统计数据, 这在欠发达国家中更加明显, 包括印度(Banerjee and Piketty (2005))和中国(王小鲁(2007)). 低收入群体因无家可归等现象也存在抽样不足或回复率偏低的问题. 这些问题显然会给统计或计量估算带来偏误. 罗楚亮(2019)就发现, 基于住户调查数据所得的基尼系数都存在低估.

为了解决收入数据缺失问题, 王小鲁(2010)使用了社会学中的"滚雪球法", 通过调查亲戚朋友等熟人进行核对调整, 以改善高收入样本的数据真实性. 但王有捐(2010)指出, "滚雪球法"在调查城市和调查样本的选择等方面存在主观性. 李实和罗楚亮(2011), 罗楚亮(2019)使用财富榜和高管薪酬数据弥补高收入样本的缺失. 白重恩等(2015)基于个体消费数据推算了我国居民的隐性收入, 发现不考虑隐性收入使得基尼系数明显低估. 这些尝试都借助于外部数据, 但外部数据的获取和匹配不但存在困难, 而且外部数据与微观调查数据之间一般不具有一致性.

3 分组数据还原

3.1 分组数据还原方法

Shorrocks and Wan (2009)构造了一种将分组数据"还原"为个体观察值的方法, 该方法在某一统计分布(如对数正态分布) 的假设下, 首先用分组数据估算该分布的参数(分布的期望值可以设为1), 并在此基础上产生洛伦兹曲线上的个体观测值. 然后对每组观测值进行调整, 以保证"还原"的数据的平均值与实际观察到的各组平均值相等, 同时保证整个洛伦兹曲线是平滑和单调上升的. 具体地, 将收入分组数据记为从低到高的1到$ k $组, 对应的洛伦兹曲线上的坐标为($ p_{k}^{*} $, $ L_k^* $), 其中$ p_k^* $ ($ k=1, \cdots, m $) 代表包括第$ k $组的累积人口比重, $ L_k^* $为相应的累积收入占比. 第$ k $组包含的观测值个数为$ m_{k}=n(p_{k}^{*}-p_{k-1}^*) $, 其中$ n $是还原的样本观测值的个数. $ x_{ki} $ ($ k=1, \cdots, m; i=1, \cdots, m_k $)代表组$ k $中个体收入观测值. 组$ k $的平均收入可以表达为:

$ \begin{align} {\mu_{k}^{*}=\frac{L_k^*-L_{k-1}^{*}}{p_{k}^{*}-p_{k-1}^{*}}, \quad k=1, \cdots, m.} \end{align} $

现在, 依据(2)式得到$ m-1 $个收入(对数)的标准差估算值:

$ \begin{align} {\sigma_{k}=\sigma^{-1}(p_{k}^{*})-\sigma^{-1}(L_k^*), \quad k=1, \cdots, m-1. } \end{align} $

其中$ \sigma $为标准正态分布函数(Kolenikov and Shorrocks (2005)). 接着求这$ m-1 $个标准差估计值的平均值, 并用以产生个体收入观察值.

最后是分两步调整这些观测值. 首先, 利用(3)和(4)式使得观察到的、真实的组收入均值$ \mu_k^* $落在每个模拟的收入组的取值区间内:

$ \begin{align} {\hat{x}_{j}=\mu_{k}^{*}+\frac{\mu_{k+1}^{*}-\mu_{k}^{*}}{\mu_{k+1}-\mu_{k}}(x_{j}-\mu_{k}) \quad k=1, \cdots, m-1, x_{j}\in [\mu_{k}, \; \; \mu_{k+1})}, \end{align} $

$ \begin{align} {\hat{x}_{j}=\frac{\mu_{1}^{*}}{\mu_{1}}x_{j}\; \; x_j<\mu_1;\; \; \hat{x}_{j}=\frac{\mu_{m}^{*}}{\mu_{m}}x_{j} \; \; x_j\geq \mu_k}. \end{align} $

然后, 利用(5)和(6) 式将每组的均值$ \mu_k $调整为实际的组收入均值$ \mu_k^* $

$ \begin{align} \qquad \quad{x_{ki}^{*}=c_{k+1}-\frac{c_{k+1}-\mu_{k}^{*}}{c_{k+1}-\hat{\mu}_{k}}(c_{k+1}-\hat{x}_{ki}), \mu_{k}^{*}>\hat{\mu}_{k}\; \; \mbox{且}\; \; k<m}, \end{align} $

$ \begin{align} {x_{ki}^{*}=c_{k}-\frac{\mu_{k}^{*}-c_{k}}{\hat{\mu}_{k}-c_{k}}(\hat{x}_{ki}-c_{k}), \mu_{k}^{*}<\hat{\mu}_{k}\; \; \mbox{或}\; \; k=m}, \end{align} $

其中,

$ \begin{align} {c_1=0; c_{k}=\frac{1}{2}(\underset{i}{\max} \hat{x}_{k-1, i}+\underset{i}{{\min}} \hat{x}_{ki}), k>1.} \end{align} $

这些调整过的观测值即可用来估算各种收入分配指标.

但收入变量不一定服从对数正态分布. 本文将评估常见的8种分布函数的"还原"的可靠性和精确度, 其中包括具有两参数的对数正态分布(Lognormal)、Gamma分布(Gamma)、Weibull分布(Weibull)和Pareto分布(Pareto); 也包括具有三参数的Singh-Maddala分布(SM)、Dagum分布(Dagum)和Beta2型分布(Beta2); 最后还包括具有四参数的Generalized Beta Distribution of the Second Kind (GB2)5. 其相应的概率密度函数及基尼系数计算公式如表 1所示.

5关于Lognormal分布函数参见Smith and Merceret (2000); 关于Gamma分布函数见Salem and Mount (1974); 关于Weibull分布函数见Menon (1963); 关于SM分布函数见Singh and Maddala (1976); Beta2分布函数见Slottje (1984); 关于Dagum分布函数见Dagum (1977); 关于GB2分布函数见McDonald (1984); 关于Pareto分布函数的相关信息可参考Krishnaji (1970).

表1   不同分布概率密度函数和基尼系数

分布类型概率密度函数基尼系数
Lognormal$\begin{aligned}f(x ; \mu, \sigma) & =\frac{1}{\sqrt{2 \pi} \sigma x} \exp \left[-\frac{1}{2 \sigma^2}(\ln x-\mu)^2\right], x>0 \\& =0 \text {, 否则 }\end{aligned} $,$ 2 \Phi\left(\frac{\sigma}{\sqrt{2}}\right)-1$
Gamma$f(x ; \alpha, \beta)=\frac{x^{\alpha-1} \exp \left(-\frac{x}{\beta}\right)}{\beta^\alpha \Gamma(\alpha)}, x>0, \alpha>0, \beta>0 $$\frac{\Gamma(\alpha+0.5)}{\Gamma(\alpha+1) \sqrt{\pi}} $
Weibull$ f(x ; \alpha, \beta)=\frac{\alpha}{\beta}\left(\frac{x}{\beta}\right)^{\alpha-1} \exp \left(\left(-\frac{x}{\beta}\right)^\alpha\right)$$1-\left(\frac{1}{2}\right)^\alpha $
SM$\begin{aligned}f(x ; a, b, q) & =\frac{a x^{a-1}}{b^a B(1, q)\left(1+\left(\frac{x}{b}\right)\right)^{1+q}}, x \geq 0 \\& =0, \text { 否则 }\end{aligned} $$1-\frac{\Gamma(q) \Gamma\left(2 q-\frac{1}{a}\right)}{\Gamma\left(q-\frac{1}{a}\right) \Gamma(2 q)} $
Beta2$\begin{aligned}f(x ; b, p, q) & =\frac{x^{p-1}}{b^p B(p, q)\left(1+\left(\frac{x}{b}\right)\right)^{p+q}}, x \geq 0 \\& =0, \text { 否则 }\end{aligned} $$\frac{2 B(2 p, 2 q-1)}{p B^2(p, q)} $
Dagum$\begin{aligned}f(x ; a, b, p) & =\frac{a x^{a p-1}}{b^{a p} B(p, 1)\left(1+\left(\frac{x}{b}\right)^a\right)^{p+1}}, x \geq 0 \\& =0, \text { 否则 }\end{aligned} $$-1+\frac{\Gamma(p) \Gamma\left(2 p+\frac{1}{a}\right)}{\Gamma\left(p+\frac{1}{a}\right) \Gamma(2 p)} $
GB2$\begin{aligned}f(x ; a, b, p, q) & =\frac{a x^{a p-1}}{b^{a p} B(p, q)\left(1+\left(\frac{x}{b}\right)^a\right)^{p+q}}, x \geq 0 \\& =0, \text { 否则 }\end{aligned} $$\begin{aligned}& \frac{B\left(2 p-\frac{1}{a}, 2 q+\frac{1}{a}\right)}{B(p, q) B\left(p+\frac{1}{a}, q-\frac{1}{a}\right)}\left\{(\frac { 1 } { p }) _ { 3 } F _ { 2 } \left[1, p+q, 2 q+\frac{1}{a} ;\right.\right. \\& p+1, 2(p+q) ; 1]-\left(\frac{1}{p+\frac{1}{a}}\right)_3 F_2\left[1, p+q, 2 p+\frac{1}{a} ;\right. \\& \left.\left.p+\frac{1}{a}+1, 2(p+q) ; 1\right]\right\}\end{aligned} $
Pareto$\begin{aligned}f\left(x ; x_{\min }, k\right) & =k \frac{x_{\min }^k}{x^{k+1}}, x \geq x_{\min } \\& =0, \text { 否则 }\end{aligned} $$\frac{k}{2 k-1} $

新窗口打开| 下载CSV


在表 1中, $ B(p, q) $为Beta函数, $ \Gamma(\alpha) $为Gamma函数, $ {}_p F_q(a, b;c;z) $为广义超几何函数. 在Gamma分布和Weibull分布中, $ \alpha $为规模参数(scale parameter), 起放大或缩小曲线的作用, 不影响分布形状, $ \beta $为形态参数(shape parameter), 影响分布的形态. 在GB2分布、SM分布、Beta2分布和Dagum分布中, $ b $为规模参数, $ a, p, q $为形态参数, $ a $影响两边尾部, $ q $仅影响右边尾部. GB2分布、SM分布、Beta2和Dagum分布之间联系极其密切. 具体而言, 对于GB2分布, 当$ p=1 $时, 它退化为SM分布; 当$ a=1 $时, 变为Beta2分布; 当$ q=1 $时, 便成了Dagum分布.

3.2 蒙特卡罗设计

基于表 1和收入分组数据, 可估算不同分布的参数, 然后生成包含任意个观测值的收入样本. 具体方法如下:

首先, 从CFPS原始样本中随机抽取样本体积为$ N $的收入观测值, 并将观察值从低到高分为$ M $组(每组观察值个数相等), 计算每一组的收入和人口占比, 这就得到了分组数据. 其次, 分别利用表 1的8种分布对分组数据进行拟合, 得到相应的参数估计值, 最后, 生成包含$ N $个收入观测值的模拟或还原样本. 在本文的部分实验中, 还将结合使用Shorrocks and Wan (2009)的迭代法(见上文).

重复以上过程$ T $次. 在本文中, $ N $取10000, $ T $取100或200, $ M $取5或10.

3.3 还原效果评估

参考Shorrocks and Wan (2009)的做法, 本文采用数值和指标比较两种方法对"还原"效果进行评估.

数值比较的具体方法为, 将真实收入数据与还原的收入数据分别从小到大排列, 计算洛伦兹曲线上每个个体所对应的收入份额偏差, 再对这一偏差取绝对值, 然后进行加总得出加总偏差6, 最后计算出$ T $次模拟的平均加总偏差. 收入份额的具体计算公式为:

$ \begin{align} {{\rm share}^i=\frac{{\rm income}_i}{\sum\limits_{j=1}^{N}{\rm income}_j}}, \end{align} $

6由于观察结果以收入份额表示, 平均绝对百分比偏差的值与样本量$ N $相关, 当样本量加倍时, 平均绝对百分比偏差将减半, 而绝对偏差之和并不会随样本量的改变而变化, 因此此处采用绝对收入份额的偏差总和来度量拟合偏差.

其中$ {\rm income}_i $代表按收入从低到高排序后第$ i $位个体的收入. 在计算偏差时, 可以对不同分位进行加总:

$ \begin{align} {{\rm share}\_{\rm bias_{local}}=\sum\limits_{i=n_{1}}^{n_{2}}\left| {\rm share}_{i}^{{\rm Simulate}}-{\rm share}_{i}^{{\rm Actual}}\right|}, \end{align} $

$ \begin{align} {{\rm share}\_{\rm bias_{global}}=\sum\limits_{i={1}}^{N}\left| {\rm share}_{i}^{{\rm Simulate}}-{\rm share}_{i}^{{\rm Actual}}\right|}, \end{align} $

其中, 上标Actual和Simulate分别表示真实数据和还原出的数据. 本文中的分位加总在十分位内进行. 比如, 当$ n_1=1001 $, $ n_2=2000 $时, 公式(9)表示的就是第二分位内收入份额偏差的加总.

最后, 我们计算多次模拟下的平均总和偏差:

$ \begin{align} {{\rm Mean}\_{\rm share}\_{\rm bias}=\sum\limits_{t=1}^{T}{\rm share}\_{\rm bias}_{t}}. \end{align} $

指标比较方面, 本文考虑收入不均、等贫困发生率和中等收入群体占比三个指标的精确度:

1) 本文采用最常用的度量不均等的指标——基尼系数(Gini).

2) 贫困发生率. 本文采用三条贫困线估算贫困发生率. Poverty2300代表基于中国官方贫困线(以2010年价格计算的、每人每年2300元)计算的贫困发生率. Poverty19和Poverty32分别为世界银行2011年确定的国际极度贫困标准(1.9美元/人/天)和国际贫困标准(3.2美元/人/天)下的贫困发生率.

3) 中等收入群体占比. 中等收入群体的界定可以使用绝对标准或相对标准. 绝对标准方面, 本文根据国家统计局的"以中国典型的三口之家年收入在10万元$ \sim $ 50万元之间7"的做法, 将人均年收入介于3.33万与16.7万之间的定义为中等收入群体, 并计算其人口占比(Mid1). 就相对标准而言, 较为常见的做法是使用收入中位数的75%$ \sim $125% (Pressman (2010), 刘志国和马健(2016), 龙莹(2015))或67%$ \sim $200% (Grabka et al. (2016)). 本文选择75%$ \sim $125%作为中等收入的标准, 由此测算中等收入群体占比的另一指标(Mid2).

7见国家统计局局长就2018年国民经济运行情况答记者问, 网址: http://www.stats.gov.cn/tjsj/sjjd/201901/t20190121_1645944.html.

使用指标法进行评估, 可以计算多次模拟下的平均绝对百分比误差(mean absolute percentage error, MAPE), 其计算公式如下:

${\text{MAPE}} = \sum\limits_{t = 1}^T {\frac{{|{\text{Index}}_t^{{\text{Simulate}}} - {\text{Index}}_t^{{\text{Actual}}}|}}{{{\text{Index}}_t^{{\text{Actual}}}}}} *100% , $

其中$ {\rm Index}_{t}^{{\rm Actual}} $为第$ t $次模拟中基于真实收入数据所得的指标, $ {\rm Index}_{t}^{{\rm Simulate}} $则为对应的基于"还原"数据获得的指标.

4 评估结果

4.1 不同分布假设下的还原效果比较

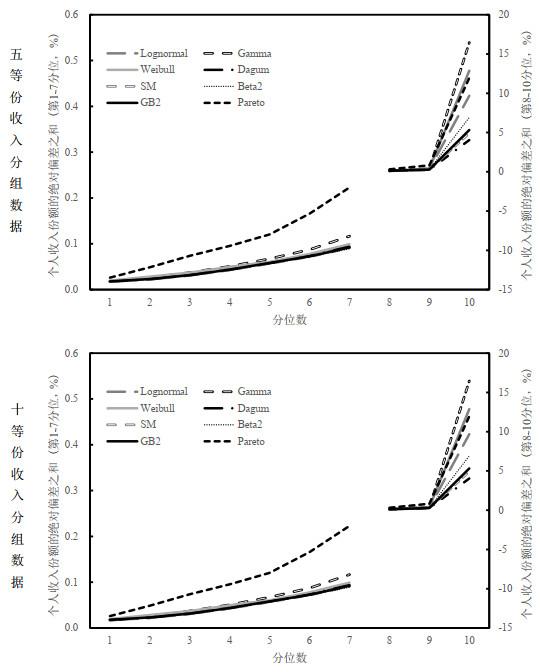
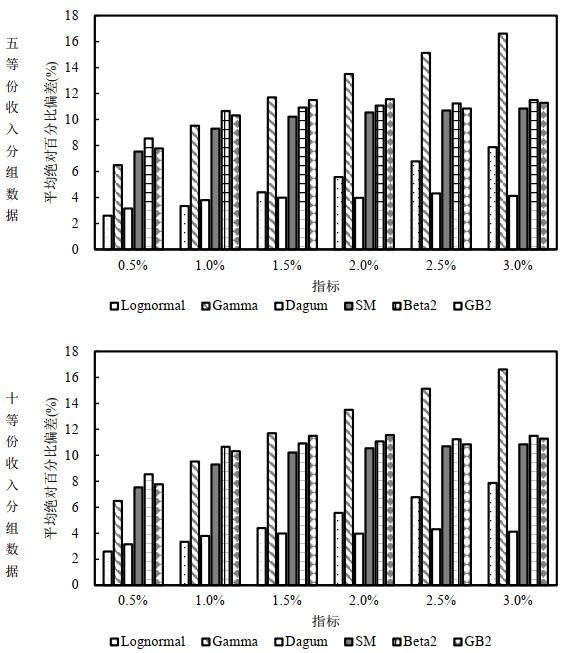
本文首先使用前文提出的方法基于分组数据获得了还原样本, 然后将其与真实样本进行分段比较, 考察每十分位所对应的收入份额的绝对偏差之和, 结果如图 1所示. 图中可以看出还原样本的收入份额绝对偏差大致随着分位的增大而增加. 不管基于何种分布, 还原样本在第1至第8分位内的偏差都较小, 而第9和第10分位内的偏差则明显较大. 总体来说, Dagum分布表现最优, 而Pareto分布、Gamma分布和Weibull分布的整体还原效果欠佳, 无论是在低分位还是高分位上偏差都明显高于其他分布. 在第1至第8分位内Lognormal、Dagum、SM、Beta2、GB2分布的偏差相差很小且都处于较低水平, 而在第9和第10分位内, 不管是五等份分组还是十等份分组数据, 采用Dagum分布所得还原样本的偏差都是最小的, 第10分位内的个人收入份额的绝对偏差小于4个百分点, 总体收入份额的绝对偏差之和也在5个百分点以内.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   不同分布假设下个人收入份额的绝对偏差之和


具体而言, 当收入数据为五等份分组形式时, 基于Dagum分布"还原"出的样本在第9分位内的收入份额的绝对偏差之和仅为0.32个百分点, SM分布和GB2分布的结果次之, 分别为0.47和0.51个百分点, 而Gamma、Weibull和Pareto分布的相应偏差都超过了3个百分点. 第10分位内收入份额的绝对偏差之和的对比更加明显, Dagum分布的偏差低至5.14个百分点, 而Gamma、Weibull和Pareto分布的偏差都在13个百分点以上. 如果计算总体收入份额的绝对偏差之和, 会发现表现较好的依然是Dagum、SM和GB2分布, 其对应的结果分别为4.97、6.10、6.30个百分点. 而当收入数据为十等份分组时, Dagum、SM和GB2分布的收入份额的绝对偏差之和分别为4.76、5.64、6.06个百分点, 总体偏差相较于五等份分组的情况都有一定程度的降低, 但各分布偏差大小的排序均未发生改变.

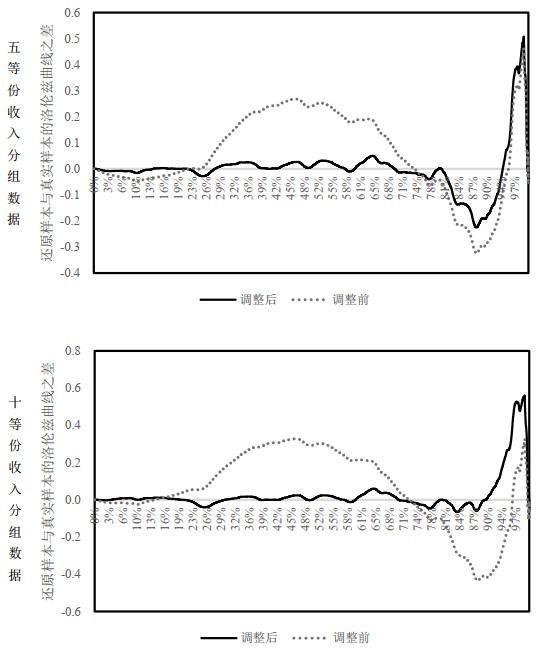
图 2绘制了基于Dagum分布进行的单次模拟中"还原"的洛伦兹曲线与真实洛伦兹曲线之间的相对偏差. 其中"调整后"表示的是经过迭代法调整后的样本, "调整前"表示未经迭代的样本, 可以看出迭代法调整后总体偏差情况有所改善.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   真实样本与还原样本的洛伦兹曲线之差


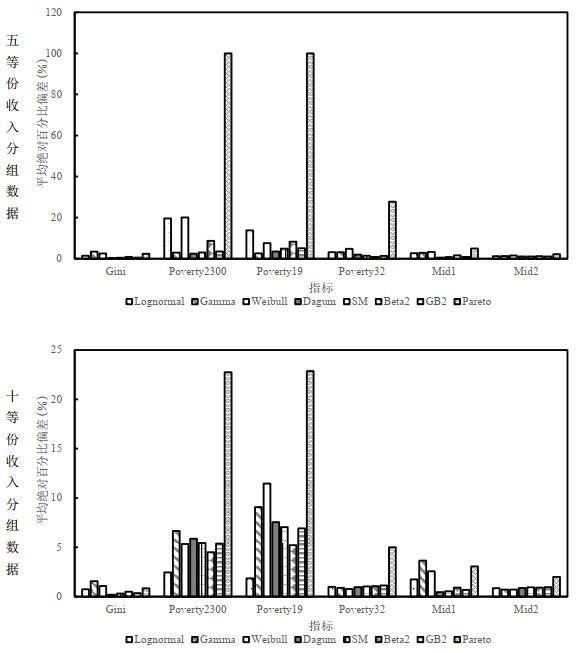
图 3报告了指标偏差. 就基尼系数而言, 不论是五等份分组还是十等份分组数据, Dagum分布的表现都是最好的, 两种分组情况下模拟值与实际值的平均绝对百分比偏差分别为0.23%和0.20%. Weibull、Gamma和Pareto分布的表现则较差. 这与图 1所反映的信息是相对应的, 由于基尼系数的偏差与收入份额偏差联系紧密, 因此收入份额绝对偏差越大的分布, 其基尼系数的估算偏差一般也较大.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同分布假设下各指标平均绝对百分比偏差


从贫困发生率的偏差来看, 在不同的分组数据、不同贫困标准下, 各分布的平均偏差表现有所不同. 在五等份分组数据中, Gamma、Dagum、SM和GB2分布表现较好, 而对于十等份分组数据来说, Lognormal分布有较为明显的优势. 考虑到十等份分组数据下各分布结果的偏差都偏小, 此处更加关注五等份分组数据的评估结果. 具体到各个贫困发生率的指标上, 在五等份分组数据下, 当以Poverty2300的平均绝对百分比偏差为标准时, Dagum分布的表现最好, 偏差为2.49%, Gamma分布和SM分布的偏差也较低, 分别为2.94%和3.02%; 以Poverty19的平均绝对百分比偏差为标准时, 表现最好的为Gamma分布, 偏差为2.65%, Dagum分布则以3.53%的偏差略次于Gamma分布; 而以Poverty32为标准时, 情况再次发生变化, Beta2分布的偏差变得最小, 仅为0.89%, 明显低于Dagum分布和Gamma分布的偏差. 不论使用哪一个贫困线下的贫困发生率作为评估标准, Pareto分布的平均绝对百分比偏差都是100%, 这是因为Pareto分布对于低收入部分的数据拟合效果较差, 导致通过模拟样本计算出的贫困率为0. 需要说明的是, 由于本文所选取的样本中贫困发生率较低, 因此图中所展示的平均绝对百分比偏差在数值上会比较大, 但其所对应的绝对偏差大多不到一个百分点.

从中等收入群体占比的偏差出发, 依然可以得出Dagum分布的表现较优这一结论. 采用Mid1指标时, Dagum分布的平均绝对百分比偏差是最小的, 五等份分组与十等份分组数据下偏差分别为0.52%和0.46%. 采用Mid2指标时, 除Pareto分布的偏差较大以外, 其他分布的表现都比较接近.

整体来看Dagum分布、SM分布、Beta2分布和GB2分布的差别不大, 且在各评估指标下都有较好的表现, 其中Dagum分布的综合表现最优.

4.2 迭代法的效果评估

表 2上半部分展示了使用迭代法与否所获得的收入份额的绝对偏差之和的均值. 以基于五等份分组数据、重复模拟100次的情况为例, 基于Dagum分布的参数估计生成的样本与真实样本相比, 收入份额的平均绝对偏差之和为5.21个百分点, 而在进行了迭代法调整之后, 这一偏差降低到4.97个百分点. 在十等份分组数据的情况下, 迭代法调整前后的偏差分别为5.23和4.76个百分点. 可以看出, 迭代法整体上可以缩小偏差, 且这一效应在Gamma分布、Weibull分布、Pareto分布的假设下最为明显, 这可能跟这三种分布的直接拟合结果较差有关. 而在Lognormal、Dagum、SM、Beta2、GB2这五种分布下, 迭代法的优势不太明显, 但除五等份分组数据下的GB2略微增大了偏差外, 其余情况下迭代法都能够在一定程度上改善还原样本的表现.

表2   不同模拟次数下迭代法调整前后偏差情况(单位: %)

指标分组数模拟次数是否调整LognormalGammaWeibullDagumSMBeta2GB2Pareto
个人收入份额五等份分组100调整后11.8920.8117.534.976.108.566.3019.49
调整前12.6926.4232.515.216.118.776.2837.49
200调整后11.9020.7817.495.026.158.606.5019.47
调整前12.6926.3332.615.276.178.806.6837.51
十等份分组100调整后10.4917.3913.774.765.647.666.0613.85
调整前12.8727.5129.135.235.898.666.8541.55
200调整后10.5017.3813.764.825.707.695.9713.66
调整前12.8727.4129.145.305.958.696.4940.84
基尼系数五等份分组100调整后1.413.462.560.230.470.900.522.40
调整前1.1415.0820.460.490.700.950.729.98
200调整后1.403.452.550.220.480.900.552.40
调整前1.1315.0420.670.490.700.951.119.99
十等份分组100调整后0.751.561.070.200.310.500.360.84
调整前0.8617.8915.470.430.530.541.5213.34
200调整后0.751.561.070.200.310.510.340.82
调整前0.8517.8515.560.430.530.541.0213.00

新窗口打开| 下载CSV


表 2下半部分展示了不同模拟次数下基尼系数的平均绝对百分比偏差, 同样发现绝大多数情况下迭代法可以明显降低还原样本的偏差. 即使是对于Dagum、SM、GB2分布这样直接拟合效果就已经较好的分布函数, 使用迭代法调整后基尼系数的平均百分比偏差依然降低了0.2个百分点以上.

对比五等份分组与十等份分组的评估结果还可以发现, 十等份分组数据的偏差大多都小于五等份分组数据. 这与直觉相符, 即分组越细, 分组数据能够提供的信息越多, 还原样本与真实样本的偏差就越小.

此外, 前文展示的是100次模拟的结果. 表 2报告了200次模拟与100次模拟结果的对比, 可以看到二者十分接近. 以基于Dagum分布还原五等份分组数据并进行迭代法调整后的结果为例, 100次模拟下个人收入份额的平均绝对偏差之和为4.97个百分点, 而200次模拟下的对应偏差之和为5.02个百分点, 二者相差0.05个百分点. 如果关注于基尼系数的平均百分比偏差, 100次模拟与200次模拟的结果分别为0.23%和0.22%, 仅相差0.01个百分点. 这表明模拟次数达到100时还原偏差已经基本稳定在某一水平. 附录中表A3至表A18详细展示了在不同模拟次数下、迭代法前后的各分位内收入份额的平均绝对偏差和各个指标的平均绝对百分比偏差, 从中也能得到与前文分析一致的结果.

4.3 截断分组数据还原

为弥补数据缺失, 本文引入条件分布法来进行拟合. 具体来说, 设$ F(x;\theta) $为收入$ x $的分布函数, $ f(x;\theta) $为相应的概率密度函数, 其中$ \theta $为需要估计的参数. 令$ l $和$ u $分别为截断样本的最小值和最大值, 或称为截断点(truncation point). 这两个截断点所对应的截断比例分别为$ {\rm tl}=F(l;\theta) $, $ {\rm tu}=1-F(u;\theta) $.

根据数据缺失部位的不同, 可以分成以下三种情况:

1) 高位数据缺失

当仅考虑高收入数据缺失时, 实际观察到的样本中有最大点$ u $, 样本条件分布函数为:

$ \begin{align} F_c (X \leq x;\theta\mid x<u)=\frac{F(x;\theta)}{F(u, \theta)}=\frac{F(x;\theta)}{1-{\rm tu}}. \end{align} $

(13) 式的含义为, 可观测的收入分布(低于$ u $的数据) 是真实分布的一部分, 实际观察到的样本占总样本的比例为$ 1-{\rm tu} $. 此时的条件概率密度为:

$ \begin{align} {f_{c}(X\leq x;\theta\mid x<u)=\frac{f(x;\theta)}{1-{\rm tu}}}. \end{align} $

2) 低位数据缺失

当仅考虑低位数据缺失时, 实际观察到的样本由中有最小点$ l $, 样本条件分布函数为:

$ \begin{align} {F_{c}(X\leq x;\theta \mid x>l)=\frac{F(x;\theta)-F(l;\theta)}{1-F(l;\theta)}=\frac{F(x;\theta)-{\rm tl}}{1-{\rm tl}}}. \end{align} $

实际观察到的样本占总样本比例为$ 1-{\rm tl} $. 对应的条件概率分布函数为:

$ \begin{align} {f_{c}(X\leq x;\theta\mid x>l)=\frac{f(x;\theta)}{1-{\rm tl}}}. \end{align} $

3) 高低位都存在缺失

当高低位数据都存在缺失时, 实际观察到的样本有最小点$ l $和最大点$ u $, 样本条件分布函数为:

$ \begin{align} {F_{c}(X\leq x;\theta\mid l<x<u)=\frac{F(x;\theta)-F(l;\theta)}{F(u;\theta)-F(l;\theta)}=\frac{F(x;\theta)-{\rm tl}}{1-{\rm tu}-{\rm tl}}}. \end{align} $

实际观察到的样本占总样本比例为$ 1-{\rm tu}-{\rm tl} $. 对应的条件概率密度函数为:

$ \begin{align} {f_{c}(X\leq x; \theta\mid l<x<u)=\frac{f(x;\theta)}{1-{\rm tu}-{\rm tl}}}. \end{align} $

以上各式中, $ N $代表实际观察到的样本体积, $ (x_1, \cdots, x_i, \cdots, x_N) $为实际观察到的个体收入. 基于不同的分布函数, 可以通过矩估计或极大似然估计法得到参数$ \theta $, 而后获得没有截断的无条件分布. 根据Hajargasht et al. (2012)的研究, 广义矩估计方法(GMM)比最大似然估计法(MLE)更加适用于分组数据的参数估计. 据此, 本文的分布参数估计全部采用了广义矩估计方法.

具体地说, 假设已知数据高低两端的缺失比例分别为$ {\rm tl} $和$ {\rm tu} $, 可以将分布函数设定为一个截断分布:

$ \begin{align} {F_{c}(X\leq x;\theta \mid l<x<u)=\frac{F(x;\theta)-F(l;\theta)}{F(u;\theta)-F(l;\theta)}=\frac{F(x;\theta)-{\rm tl}}{1-{\rm tu}-{\rm tl}}}. \end{align} $

条件分布拟合相比于无条件分布拟合增加了两个待估参数$ {\rm tu} $和$ {\rm tl} $. 相应地, 在使用迭代法时, 处理方法也要有所变化. 在无条件分布假设下, 分组数据不存在缺失, 因此调整只需保证"还原"的数据的平均值与实际观察到的各组平均值相等. 而在数据存在截断的情况下, 每组的均值实际反映的是截断后的数据均值, 而模拟生成的样本则服从预设的完整的分布, 因此每组均值实际只包含了未被截断部分的信息. 为此本文将该样本分成前、中、后三段, 所占比例分别为$ {\rm tl} $、$ 1-{\rm tl}-{\rm tu} $和$ {\rm tu} $. 中段数据按照每组的实际均值进行调整, 前(后) 段则锚定中段的最小(大) 值进行等比例缩放, 最后将前中后三段"拼接"起来就得到了完整的样本. 这样处理的一个隐含假设是收入数据分布是连续的.

4.4 还原效果评估

同样基于CFPS2018的数据进行蒙特卡罗评估, 但此处要先对样本做不同程度的双边截断处理8, 其中截断比例分别设置为0.5%、1%、1.5%、2%、2.5%、3%. 假设两端的截断比例a%未知, 通过前述方法对数据进行还原, 再将还原样本与真实样本进行比较, 评估各分布在此方法下的表现. 根据前面的结果, Pareto分布和Weibull分布的还原表现较差, 故这里不再展示相应结果.

8现实中调查数据通常同时存在高低端的缺失, 但两端的缺失比例不一定相同, 为节省篇幅此处仅讨论了双边缺失相同比例的情况.

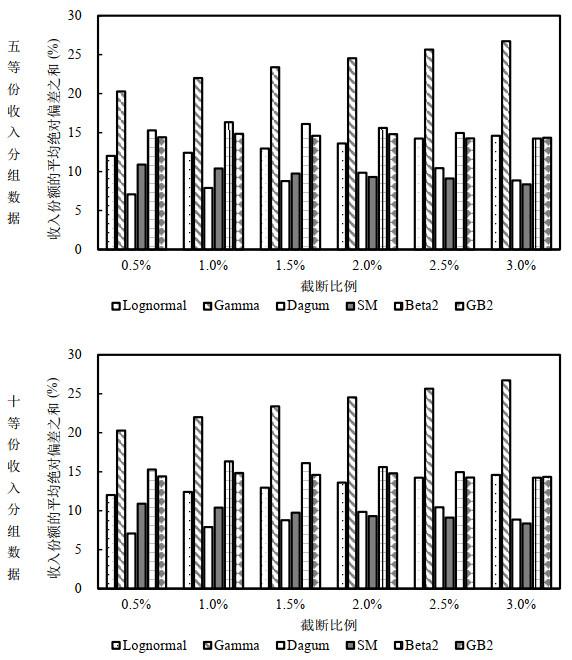
图 4展示了不同截断比例下, 不同分布函数的还原表现. 当数据为五等份分组数据时, 不论缺失比例为多少, Dagum分布的偏差都最小, 绝对偏差之和介于8$ \sim $9个百分点之间. Lognormal分布的表现次之, 绝对偏差之和在12到15个百分点之间. Gamma分的偏差最大. 十等份分组数据的结果略有不同, 当截断比例为0.5%、1%、1.5%时, Dagum分布的偏差最小, 而当截断比例在2%以上时, SM分布的偏差略小于Dagum分布. 总体来看Dagum分布在绝大多数情况下的绝对偏差之和都小于10个百分点, 还原效果较好. 从基尼系数的绝对百分比偏差来看, 五等份分组数据下的Dagum分布的整体表现也相对较好, 见图 5. 当截断比例不高于1%时, Dagum分布的偏差稍大于Lognormal分布, 但整体偏差依然处于较低水平, 且这一偏差没有随着截断比例的上升而明显增加. 十等份分组数据下, 当截断比例不高于1%时, Dagum分布的表现最好, 而随着截断比例的上升, SM分布展现出了较好的还原效果, Dagum分布略次之. 事实上, 从前文的结果中可以发现, 还原样本所得基尼系数的偏差主要取决于高位的收入份额偏差, 因此以基尼系数为标准的评估结果与以个人收入份额为标准的评估结果是基本一致的. 附录中表A1和A2展示了在不同截断比例下的贫困发生率和中等收入群体占比的平均绝对百分比偏差9. 需要注意的是, 由于本文采用了绝对百分比偏差作为评估标准, 而贫困率的绝对数值一般较低, 这会导致偏差的数值看起来较大. 如对于截断比例为0.5%的五等份分组数据, 基于Dagum分布获得的还原样本与真实样本在Poverty2300指标上的平均绝对偏差为1.77个百分点, 其平均绝对百分比偏差的数值则高达39.83%. 这主要是因为真实样本中Poverty2300指标的水平在4.5%左右, 并不代表拟合的绝对偏差过大. 因此, 尽管表A1和表A2中出现了某些较大的数值, 但结合指标的绝对水平来看, 拟合的偏差依然处于合理范围.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同截断比例下各分布个人收入份额的绝对偏差之和


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同截断比例下各分布基尼系数的平均绝对百分比偏差


9本文中贫困发生率和中等收入群体的指标使用了多个标准, 由于篇幅限制将对比结果在附录中展示.

基于表A1和A2很难选出一个最优的分布. 总体来看, 除了Lognormal分布和Gamma分布的偏差明显偏大, Dagum、SM、Beta2、GB2分布的偏差都在可接受范围内.

综合本部分的所有评估结果, 可以发现Dagum分布的总体表现是最好的, 不论怎么评估, 它都具有较小的偏差, 在收入份额占比和基尼系数的还原上具有明显的优势. SM分布总体上略逊于Dagum分布, 但同样有着不错的表现. 而其他分布则总在某些情况下偏差较大, 可能在实际应用中带来较大的误差.

表 3展示了不同情况下收入份额的平均绝对偏差之和. 可以看到, 如果数据存在截断, 但在拟合时不予考虑, 将会造成相当大的偏差. 且截断比例越大, 这一偏差越大. 如果考虑到截断问题, 使用条件分布进行拟合, 还原结果在多数情况下都有明显改善. 在此基础上再应用Shorrocks and Wan (2009)的迭代法, 偏差将进一步降低. 以截断比例为1%的五等份分组数据为例, 不考虑截断时, 收入份额的平均绝对偏差之和为15.35个百分点, 考虑截断后偏差降低到8.46个百分点, 使用迭代法进行调整后偏差进一步降为8.37个百分点. 除了偏差较小之外, 引入条件分布的还原方法还有一个明显的优点——随着截断比例的变化, 偏差的幅度能够保持相对稳定, 而不会出现因截断比例的增加导致偏差大幅升高的情况.

表3   不同模拟次数下迭代法调整前后个人收入份额的平均绝对偏差之和(单位: %)

分组数处理方法截断比例LognormalGammaDagumSMBeta2GB2
五等份分组考虑截断且进行调整0.50%12.4922.298.0214.6516.1914.93
1.00%12.6923.288.3716.7417.8817.56
1.50%13.0324.138.4317.7318.0318.81
2.00%13.5324.918.2217.9318.0618.71
2.50%14.1225.668.5217.9218.1117.76
3.00%14.7026.428.0717.9218.2818.16
考虑截断但未进行调整0.50%12.8225.348.1114.6916.3314.99
1.00%12.9125.658.4616.7617.8817.56
1.50%13.1826.038.5417.7418.0318.80
2.00%13.6426.468.3417.9318.0518.70
2.50%14.2026.948.6717.9118.0917.74
3.00%14.7527.458.2317.9018.2518.12
未考虑截断0.50%15.4722.9911.7813.9615.8016.11
1.00%17.7624.4415.3517.4018.9119.77
1.50%19.5525.5217.8519.6720.9721.86
2.00%21.1226.4419.8621.4522.5923.38
2.50%22.6027.3321.6323.0424.0424.71
3.00%23.9928.1923.2024.4625.3425.97
十等份分组考虑截断且进行调整0.50%12.0020.297.0910.9115.2814.41
1.00%12.4122.017.9010.3916.3314.85
1.50%12.9523.388.799.7416.1114.59
2.00%13.6024.559.849.3115.6014.81
2.50%14.2425.6510.449.1114.9514.26
3.00%14.6026.728.878.3614.2314.35
考虑截断但未进行调整0.50%12.8925.377.1310.9215.3214.44
1.00%13.0525.667.9210.4116.3014.83
1.50%13.3926.048.789.7716.0814.57
2.00%13.9226.489.829.3315.5714.79
2.50%14.4626.9710.459.1414.9214.24
3.00%14.7727.509.118.4314.2014.32
未考虑截断0.50%16.0120.5913.8514.8615.9216.31
1.00%19.5322.7618.3019.0319.6820.40
1.50%22.0524.3721.2521.7622.2022.70
2.00%23.9425.7023.4823.8724.1824.49
2.50%25.7026.9625.4025.7025.9226.15
3.00%27.2228.1527.0227.2627.4327.56

新窗口打开| 下载CSV


与本部分第二小节类似, 此处把模拟次数由100次增加到200次, 并观察还原结果是否存在显著差异. 表 4展示了200次模拟下, 依照条件分布法拟合并进行迭代法调整所得到的个人收入份额的平均绝对偏差之和, 结果依然与100次模拟的情况接近.

表4   200次模拟下个人收入份额的平均绝对偏差之和(单位: align="left")

分组数截断比例LognormalGammaDagumSMBeta2GB2
五等份分组0.512.5122.257.9914.5516.1514.90
1.012.7123.238.5616.5317.7017.39
1.513.0424.088.4617.5517.8318.58
2.013.5324.858.4617.6917.8318.42
2.514.1025.598.5817.6317.9017.47
3.014.6426.358.0817.6018.1117.74
十等份分组0.512.0020.277.0810.8415.2714.63
1.012.4121.988.0010.2816.2214.82
1.512.9423.348.979.6915.9814.60
2.013.5924.5010.029.3115.4814.76
2.514.2125.6010.469.0714.7714.27
3.014.5426.668.868.2114.0514.24

新窗口打开| 下载CSV


5 方法应用

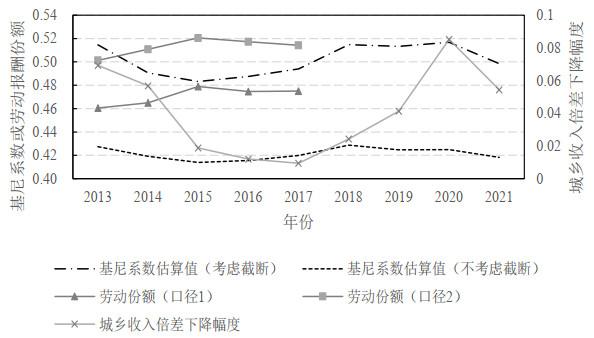
图 6展示了采用Dagum分布还原全国居民收入分组数据计算出的基尼系数, 可以看出考虑截断的基尼系数估算值比不考虑截断的估计值要高, 但二者趋势相似. 图中居民收入基尼系数的变化可以划分为三阶段, 其中2013–2015年基尼系数明显下降, 2015–2018年开始提升, 之后又呈缓慢下降趋势. 这与城乡收入倍差的降幅在趋势上基本一致. 城乡收入差距是总体收入差距的重要组成部分(Wan (2007)), 2013年至今城乡收入倍差连年下降, 较高降幅与收入差距缩小的对应在一定程度上体现了基尼系数测算结果的可靠性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   全国基尼系数与劳动报酬份额趋势

数据来源: 基尼系数估算值为作者根据国家统计局公布的收入分组数据测算, 劳动报酬份额数据来自张军等(2022).


另外, 劳动报酬份额也是反映收入差距的重要指标. 根据张军等(2022)的测算, 不论是基于《中国统计年鉴》数据(口径1)还是中国投入产出表数据(口径2)算出的2013–2017年的劳动报酬份额均以2015年为转折点先上升后下降, 这与图中所呈现的收入差距变化情况恰好吻合.

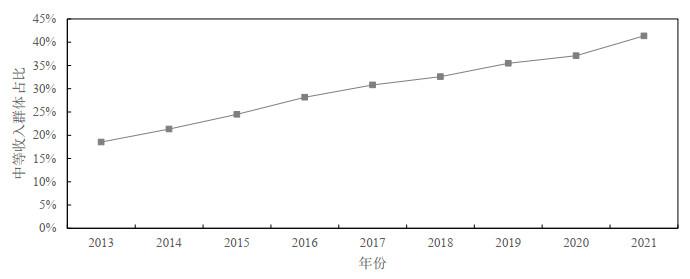
图 7则展示了在考虑截断情况下采用Dagum分布还原分组数据计算出的中等收入群体占比, 收入参考标准为国家统计局的"中国典型的三口之家的年收入在10$ \sim $50万元之间". 据测算, 2013–2021年中等收入群体占比以平均每年1.9个百分点的速率不断增加, 到2021年, 中等收入人群已经达到5.4亿人, 占比约为38%10.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   全国中等收入群体占比趋势

数据来源: 作者根据国家统计局公布的分组数据测算.


10各年中等收入群体的标准为以2017年为基期根据居民消费价格指数调整所得.

受篇幅所限, 本文无法对相关实际应用结果进行全面展示. 后续研究可以基于本文的发现, 对中国不同层面的的收入不均等、中等收入群体占比、贫困等收入分配问题进行更为详细的分析, 或者通过控制这些重要变量获得更为可靠的研究发现与结论.

6 小结

不均等、贫困和中等收入群体占比等收入分配指标, 不但自身非常重要, 而且是影响众多经济关系的关键变量之一, 但相关数据的缺失不仅阻碍了收入分配领域的研究进展, 还使得实证研究无法将其纳入相关研究框架. 幸运的是, 不少国家和地区公布收入分组数据, 为通过使用Shorrocks and Wan (2009)的方法还原数据, 然后估算这些指标提供了可能.

但是, Shorrocks and Wan (2009)的方法依赖于预设的统计分布函数, 而且没有考虑数据缺失问题. 基于CFPS2018数据进行蒙特卡罗实验, 本文首先评估了常用分布函数的表现, 结果发现Dagum分布的表现相对较优. 此外, 本文还发现, Shorrocks and Wan (2009)提出的迭代法可以改善还原数据的可靠性. 接着, 本文引入条件分布以填补数据缺失. 蒙特卡罗实验结果显示, 使用条件分布可以在相当程度上解决数据截断问题, 而且Dagum分布的表现最佳. 最后, 本文基于国家统计局公布的收入分组数据估算了中国的基尼系数和中等收入群体占比指标, 并据此进行了简单的分析讨论.

应当说明的是, 本文的研究具有一定的局限性. 一是假定不同收入群体的数据服从同一分布; 二是除截断部分(低收入或高收入部分) 以外, 不存在或少有其他数据问题. 一般来说, 分布函数的参数越多, 其还原效果越好. 但由于分组数据所能提供的信息有限, 过多的参数可能导致拟合结果不稳定, 这一问题在使用条件分布法时尤为突出. 如果能够通过其他途径预先获得数据缺失的比例, 应该可以得到更为可靠的还原数据.

附录

表A1   不同截断比例下贫困率的平均绝对百分比偏差(单位: %)

分组数指标截断比例LognormalGammaDagumSMBeta2GB2
五等份分组Poverty23000.50%28.5281.8939.8321.0610.3714.04
1.00%35.6771.1933.3822.805.679.67
1.50%42.0461.2230.3922.406.919.16
2.00%47.7251.7826.2819.878.0111.43
2.50%52.8042.6920.9316.789.8713.24
3.00%56.9533.8517.0413.4011.6912.48
Poverty190.50%22.2463.7229.3614.767.7511.15
1.00%29.2655.4324.3316.145.467.57
1.50%35.4847.6021.7816.036.978.02
2.00%41.0740.0918.2613.958.3010.42
2.50%46.1032.8214.5011.3510.1511.63
3.00%50.2225.6711.368.6811.8011.57
Poverty320.50%2.9937.3917.1510.476.227.16
1.00%8.5433.1114.0411.263.515.37
1.50%13.5528.9112.2310.983.314.75
2.00%18.2424.769.929.493.295.18
2.50%22.6320.737.767.644.226.11
3.00%26.3116.795.815.895.345.94
十等份分组Poverty23000.50%17.6095.6318.308.117.997.78
1.00%29.7682.2911.605.609.698.73
1.50%39.5270.217.165.5613.6611.97
2.00%47.6559.027.558.7318.8418.12
2.50%54.1548.3210.9813.4224.4224.34
3.00%57.3937.7312.9617.8930.1230.65
Poverty190.50%12.8973.7611.494.828.327.10
1.00%23.1963.936.754.389.848.42
1.50%32.6554.395.586.4313.6812.06
2.00%40.7545.388.4610.2218.3117.69
2.50%47.1936.7512.7614.7723.1923.17
3.00%50.4328.2114.8618.8228.2128.63
Poverty320.50%5.1735.096.973.712.002.62
1.00%9.8431.294.302.522.862.86
1.50%14.2427.592.852.444.624.28
2.00%18.3124.053.784.066.976.85
2.50%22.3721.336.086.599.829.92
3.00%24.8918.037.489.1413.1313.31

新窗口打开| 下载CSV


表A2   不同截断比例下中等收入占比的平均绝对百分比偏差(单位: %)

分组数指标截断比例LognormalGammaDagumSMBeta2GB2
五等份分组Mid10.50%0.803.811.960.661.011.02
1.00%2.902.821.270.631.491.24
1.50%4.422.560.970.581.451.22
2.00%5.532.610.870.591.551.37
2.50%6.462.831.060.631.801.63
3.00%7.143.151.390.632.031.78
Mid20.50%1.274.802.921.541.231.45
1.00%1.604.042.971.531.141.21
1.50%1.973.223.041.421.191.23
2.00%2.442.423.061.311.231.34
2.50%2.951.713.011.261.281.21
3.00%3.411.242.931.201.341.22
十等份分组Mid10.50%1.121.970.930.651.731.42
1.00%2.871.080.470.881.851.56
1.50%4.191.110.881.352.111.94
2.00%5.191.501.681.942.532.51
2.50%6.022.022.552.693.183.22
3.00%6.692.612.963.353.883.93
Mid20.50%0.815.922.431.380.731.03
1.00%1.064.972.451.340.690.86
1.50%0.914.022.541.360.720.72
2.00%0.833.052.751.500.780.73
2.50%1.172.072.611.650.860.83
3.00%1.571.202.191.480.940.95

新窗口打开| 下载CSV


表A3   调整后各分位内收入份额平均绝对偏差(%) (五等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.020.020.030.020.020.020.020.04
20.040.030.050.020.020.030.020.08
30.050.040.070.030.030.040.030.13
40.060.050.090.050.040.040.040.20
50.080.070.110.060.060.060.060.26
60.100.100.140.070.070.080.070.36
70.130.140.200.090.100.100.100.50
80.290.430.450.140.150.190.141.04
91.443.903.220.320.470.900.513.20
109.6816.0313.184.165.147.105.3113.69
total11.8920.8117.534.976.108.566.3019.49

新窗口打开| 下载CSV


表A4   调整前各分位内收入份额平均绝对偏差(%) (五等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.040.070.670.030.020.020.020.14
20.070.161.100.040.030.040.030.50
30.110.441.360.050.040.040.040.86
40.130.791.570.070.050.050.051.19
50.151.171.770.090.060.070.061.62
60.181.581.860.110.080.090.082.11
70.222.021.960.140.100.130.102.84
80.602.432.100.190.150.310.143.74
91.642.723.730.330.491.010.534.49
109.5715.0416.424.165.097.015.2520.01
total12.6926.4232.515.216.118.776.2837.49

新窗口打开| 下载CSV


表A5   调整后各分位内收入份额平均绝对偏差(%) (十等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.020.020.020.020.020.020.020.03
20.020.030.030.020.020.020.020.05
30.040.040.040.030.030.030.030.07
40.050.050.050.040.040.040.040.10
50.060.070.060.060.060.060.060.12
60.080.090.080.070.070.070.070.17
70.090.120.100.090.090.090.090.22
80.120.160.130.120.120.120.120.31
90.330.370.390.260.270.290.280.83
109.6816.4612.874.044.926.925.3211.95
total10.4917.3913.774.765.647.666.0613.85

新窗口打开| 下载CSV


表A6   调整前各分位内收入份额平均绝对偏差(%) (十等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.050.050.310.020.020.030.060.16
20.100.300.660.050.030.040.090.53
30.120.651.060.060.040.050.110.92
40.150.991.240.070.050.060.111.25
50.191.351.480.090.060.070.121.69
60.221.711.590.120.080.100.142.25
70.262.061.680.160.110.150.173.09
80.572.341.920.200.170.280.224.02
91.642.624.150.350.420.970.474.84
109.5815.4415.044.094.916.905.3722.79
total12.8727.5129.135.235.898.666.8541.55

新窗口打开| 下载CSV


表A7   调整后各指标平均绝对百分比偏差(%) (五等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini1.413.462.560.230.470.900.522.40
Poverty230019.652.9420.082.493.028.683.49100.00
Poverty1913.782.657.613.534.918.255.11100.00
Poverty323.183.194.801.991.440.891.3827.77
Mid12.662.883.300.520.801.630.854.93
Mid21.221.271.571.121.101.211.102.20

新窗口打开| 下载CSV


表A8   调整前各指标平均绝对百分比偏差(%) (五等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini1.1415.0820.460.490.700.950.729.98
Poverty230025.9824.19308.544.372.8210.683.43100.00
Poverty1920.1413.67243.092.304.4810.225.11100.00
Poverty321.311.35135.962.031.691.171.67100.00
Mid13.0738.5917.161.510.721.850.6147.69
Mid26.765.7639.264.331.862.831.3770.09

新窗口打开| 下载CSV


表A9   调整后各指标平均绝对百分比偏差(%) (十等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini0.751.561.070.200.310.500.360.84
Poverty23002.466.675.335.875.444.495.3822.75
Poverty191.869.0811.477.557.045.226.9222.86
Poverty320.980.880.780.961.021.061.135.01
Mid11.753.652.570.460.550.910.683.06
Mid20.860.710.710.880.940.910.961.99

新窗口打开| 下载CSV


表A10   调整前各指标平均绝对百分比偏差(%) (十等份分组数据, 模拟100次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini0.8617.8915.470.430.530.541.5213.34
Poverty230021.843.50335.902.183.839.885.44120.44
Poverty1916.215.19263.914.506.199.387.70114.48
Poverty322.7812.58145.053.852.581.163.86106.07
Mid12.5241.022.092.180.891.312.4750.07
Mid27.541.7041.434.962.172.973.7066.62

新窗口打开| 下载CSV


表A11   调整后各分位内收入份额平均绝对偏差(%) (五等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.020.020.030.020.020.020.020.04
20.040.020.050.020.020.030.020.08
30.050.040.070.030.030.040.030.13
40.060.050.090.050.040.040.040.20
50.080.070.110.060.060.060.060.26
60.100.100.140.070.070.080.070.36
70.130.140.200.090.100.100.100.50
80.290.440.450.140.150.190.151.04
91.443.903.200.310.470.900.543.19
109.6916.0013.154.225.207.145.4713.66
total11.9020.7817.495.026.158.606.5019.47

新窗口打开| 下载CSV


表A12   调整前各分位内收入份额平均绝对偏差(%) (五等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.040.070.660.030.020.020.050.14
20.070.161.080.040.030.040.050.50
30.110.441.350.060.040.040.060.86
40.130.791.570.070.050.050.071.19
50.151.171.780.090.060.070.081.61
60.171.581.880.120.080.090.092.12
70.222.011.980.140.100.130.112.85
80.592.412.110.190.150.300.153.74
91.632.713.730.330.481.010.554.49
109.5814.9916.464.225.157.055.4720.01
total12.6926.3332.615.276.178.806.6837.51

新窗口打开| 下载CSV


表13   调整后各分位内收入份额平均绝对偏差(%) (十等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.020.020.020.020.020.020.020.03
20.020.030.030.020.020.020.020.05
30.040.040.040.030.030.030.030.07
40.050.050.050.040.040.040.040.10
50.060.070.060.060.060.060.060.12
60.080.090.080.070.070.070.070.16
70.090.120.100.090.090.090.090.22
80.120.160.140.130.120.120.120.32
90.320.370.380.250.270.290.270.83
109.7016.4512.874.114.976.965.2411.77
total10.5017.3813.764.825.707.695.9713.66

新窗口打开| 下载CSV


表14   调整前各分位内收入份额平均绝对偏差(%) (十等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
10.050.050.310.020.020.030.040.15
20.100.300.660.050.030.040.060.52
30.120.641.060.060.040.050.070.90
40.150.991.240.070.050.060.081.23
50.181.351.480.090.060.070.091.67
60.221.711.590.120.080.100.102.23
70.262.051.680.160.110.150.143.06
80.562.331.920.200.170.270.193.99
91.632.604.140.350.420.970.454.78
109.6015.4015.064.164.976.955.2622.31
total12.8727.4129.145.305.958.696.4940.84

新窗口打开| 下载CSV


表A15   调整后各指标平均绝对百分比偏差(%) (五等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini1.403.452.550.220.480.900.552.40
Poverty230019.622.9220.462.312.828.513.80100.00
Poverty1913.822.487.633.434.858.205.30100.00
Poverty323.183.224.892.011.460.911.4427.80
Mid12.703.003.290.580.861.670.955.02
Mid21.141.251.521.081.041.131.052.20

新窗口打开| 下载CSV


表A16   调整前各指标平均绝对百分比偏差(%) (五等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini1.1315.0420.670.490.700.951.119.99
Poverty230025.9724.65312.274.522.6310.473.77100.00
Poverty1920.2013.95246.072.074.3310.145.59100.00
Poverty321.391.32137.272.031.711.202.17100.00
Mid12.8838.2116.801.620.701.700.9447.78
Mid26.625.6539.644.451.902.722.6470.30

新窗口打开| 下载CSV


表A17   调整后各指标平均绝对百分比偏差(%) (十等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini0.751.561.070.200.310.510.340.82
Poverty23002.496.455.115.705.294.425.2223.31
Poverty191.809.0711.397.506.995.186.8822.98
Poverty321.010.910.770.981.061.101.115.02
Mid11.783.892.600.530.630.990.702.68
Mid20.890.760.770.870.950.930.961.97

新窗口打开| 下载CSV


表A18   调整前各指标平均绝对百分比偏差(%) (十等份分组数据, 模拟200次)

分布LognormalGammaWeibullDagumSMBeta2GB2Pareto
Gini0.8517.8515.560.430.530.541.0213.00
Poverty230021.803.60338.482.013.629.714.66110.22
Poverty1916.244.89265.514.376.089.327.01107.24
Poverty322.7712.44145.793.832.591.173.18103.04
Mid12.3640.641.862.310.991.161.7249.91
Mid27.411.6441.395.092.252.862.7966.97

新窗口打开| 下载CSV


参考文献

白重恩, 唐燕华, 张琼,

中国隐性收入规模估计——基于扩展消费支出模型及数据的解读

[J]. 经济研究, 2015, 50 (6): 4- 18.

URL     [本文引用: 1]

Bai C E , Tang Y H , Zhang Q ,

Estimating the Size of Hidden Income in China-An Interpretation Based on the Extended Consumption Expenditure Model and Data

[J]. Economic Research, 2015, 50 (6): 4- 18.

URL     [本文引用: 1]

陈春良, 易君健,

收入差距与刑事犯罪: 基于中国省级面板数据的经验研究

[J]. 世界经济, 2009, 32 (1): 13- 25.

URL     [本文引用: 1]

Chen C L , Yi J J ,

Income Disparity and Criminal Crime: An Empirical Study Based on Provincial Panel Data in China

[J]. World Economy, 2009, 32 (1): 13- 25.

URL     [本文引用: 1]

陈建东, 罗涛, 赵艾凤,

收入分布函数在收入不平等研究领域的应用

[J]. 统计研究, 2013, 30 (9): 79- 86.

DOI      [本文引用: 1]

Chen J D , Luo T , Zhao A F ,

Application of Income Distribution Function in the Field of Income Inequality Research

[J]. Statistical Research, 2013, 30 (9): 79- 86.

DOI      [本文引用: 1]

胡志军, 刘宗明, 龚志民,

中国总体收入基尼系数的估计: 1985-2008

[J]. 经济学(季刊), 2011, 10 (4): 1423- 1436.

URL     [本文引用: 2]

Hu Z J , Liu Z M , Gong Z M ,

Estimation of the Gini Coeffcient of Overall Income in China: 1985-2008

[J]. Economics (Quarterly), 2011, 10 (4): 1423- 1436.

URL     [本文引用: 2]

李实, 罗楚亮,

中国收入差距究竟有多大?——对修正样本结构偏差的尝试

[J]. 经济研究, 2011, 46 (4): 68- 79.

URL     [本文引用: 2]

Li S , Luo C L ,

How Big is the Income Gap in China?-An Attempt to Correct for Sample Structure Bias

[J]. Economic Research, 2011, 46 (4): 68- 79.

URL     [本文引用: 2]

刘志国, 马健,

谁的上升空间受到了挤压: 收入流动性角度的分析

[J]. 经济学动态, 2016, (8): 53- 60.

URL     [本文引用: 1]

Liu Z G , Ma J ,

Whose Upside is Squeezed: An Analysis from the Perspective of Income Mobility

[J]. Economic Dynamics, 2016, (8): 53- 60.

URL     [本文引用: 1]

龙莹,

中等收入群体比重变动的因素分解——基于收入极化指数的经验证据

[J]. 统计研究, 2015, 32 (2): 37- 43.

DOI      [本文引用: 1]

Long Y ,

Factor Decomposition of the Change in the Share of Middle-income Group-Empirical Evidence Based on Income Polarization Index

[J]. Statistical Research, 2015, 32 (2): 37- 43.

DOI      [本文引用: 1]

陆铭, 陈钊, 万广华,

因患寡, 而患不均——中国的收入差距、投资、教育和增长的相互影响

[J]. 经济研究, 2005, (12): 4- 14.

URL     [本文引用: 1]

Lu M , Chen Z , Wan G H ,

Unevenness Because of Scarcity-The Interplay of Income Disparity, Investment, Education and Growth in China

[J]. Economic Research, 2005, (12): 4- 14.

URL     [本文引用: 1]

罗楚亮,

高收入人群缺失与收入差距低估

[J]. 经济学动态, 2019, (1): 15- 27.

URL     [本文引用: 3]

Luo C L ,

The Absence of High-income People and the Underestimation of Income Disparity

[J]. Economic Dynamics, 2019, (1): 15- 27.

URL     [本文引用: 3]

祁磊, 艾小青,

分组数据下收入基尼系数的计算误差分析

[J]. 统计与决策, 2021, 37 (15): 43- 46.

URL     [本文引用: 1]

Qi L , Ai X Q ,

Error Analysis of the Calculation of Income Gini Coeffcient Under Grouped Data

[J]. Statistics and Decision Making, 2021, 37 (15): 43- 46.

URL     [本文引用: 1]

汪晨, 万广华, 吴万宗,

中国减贫战略转型及其面临的挑战

[J]. 中国工业经济, 2020, (1): 5- 23.

URL     [本文引用: 1]

Wang C , Wan G H , Wu W Z ,

China's Poverty Reduction Strategy Transformation and the Challenges it Faces

[J]. China Industrial Econom, 2020, (1): 5- 23.

URL     [本文引用: 1]

王小鲁,

灰色收入拉大居民收入差距

[J]. 中国改革, 2007, (7): 8- 12.

URL     [本文引用: 2]

Wang X L ,

Gray Income Widens the Income Gap Among Residents

[J]. China Reform, 2007, (7): 8- 12.

URL     [本文引用: 2]

王小鲁, (2010). 灰色收入与国民收入分配[J]. 比较, 第48辑.

[本文引用: 1]

Wang X L, (2010). Gray Income and National Income Distribution[J]. Comparative, No. 48.

[本文引用: 1]

王有捐, (2010). 也谈城镇居民收入的统计与调查方法——与王小鲁博士及其课题组关于调查推算方法的商榷[C]//中国收入分配: 探究与争论: 284-289.

[本文引用: 1]

Wang Y J, (2010). Also on the Statistics and Survey Methods of Urban Residents' Income-Discussion with Dr. Wang Xiaolu and His Group on the Survey Projection Methods[C]//Income Distribution in China: Exploration and Debate: 284-289.

[本文引用: 1]

张军, 吴桂英, 张吉鹏,

中国省际物质资本存量估算: 1952-2000

[J]. 经济研究, 2004, (10): 35- 44.

URL     [本文引用: 1]

Zhang J , Wu G Y , Zhang J P ,

Estimation of Inter-provincial Physical Capital Stock in China: 1952-2000

[J]. Economic Research, 2004, (10): 35- 44.

URL     [本文引用: 1]

张军, 张席斌, 张丽娜,

中国劳动报酬份额变化的动态一般均衡分析

[J]. 经济研究, 2022, 57 (7): 26- 44.

URL     [本文引用: 2]

Zhang J , Zhang X B , Zhang L N ,

Dynamic General Equilibrium Analysis of the Change of Labor Compensation Share in China

[J]. Economic Research, 2022, 57 (7): 26- 44.

URL     [本文引用: 2]

张萌旭, 陈建东, 蒲明,

城镇居民收入分布函数的研究

[J]. 数量经济技术经济研究, 2013, 30 (4): 57- 71.

URL     [本文引用: 1]

Zhang M X , Chen J D , Pu M ,

Research on the Distribution Function of Urban Residents' Income

[J]. Quantitative Economics and Technical Economics Research, 2013, 30 (4): 57- 71.

URL     [本文引用: 1]

郑世林, 杨梦俊,

中国省际无形资本存量估算: 2000-2016年

[J]. 管理世界, 2020, 36 (9): 67- 81.

URL     [本文引用: 1]

Zheng S L , Yang M J ,

Estimation of Inter-provincial Intangible Capital Stock in China: 2000 to 2016

[J]. Management World, 2020, 36 (9): 67- 81.

URL     [本文引用: 1]

Banerjee A , Piketty T ,

Top Indian Incomes, 1922-2000

[J]. The World Bank Economic Review, 2005, 19 (1): 1- 20.

[本文引用: 1]

Burkhauser R V , Feng S , Jenkins S P , Larrimore J ,

Estimating trends in US income Inequality Using the Current Population Survey: The Importance of Controlling for Censoring

[J]. The Journal of Economic Inequality, 2011, 9 (3): 393- 415.

[本文引用: 1]

Dagum C ,

A New Model of Personal Income Distribution: Specification and Estimation

[J]. Economie Appliquée, 1977, 30, 413- 437.

[本文引用: 3]

Deaton A ,

Measuring Poverty in a Growing World (or Measuring Growth in a Poor World)

[J]. Review of Economics and Statistics, 2005, 87 (1): 1- 19.

[本文引用: 1]

Gastwirth J L ,

The Estimation of the Lorenz Curve and Gini Index

[J]. Review of Economics and Statistics, 1972, 54, 306- 316.

[本文引用: 2]

Grabka M , Goebel J , Schröder C , Schupp J ,

Shrinking Share of Middle-income Group in Germany and the US

[J]. DIW Economic Bulletin, 2016, 6 (18): 199- 210.

[本文引用: 1]

Hajargasht G , Griffths W E , Brice J , Rao D S , Chotikapanich D ,

Inference for Income Distributions Using Grouped Data

[J]. Journal of Business & Economic Statistics, 2012, 30, 563- 575.

[本文引用: 1]

Kakwani N ,

On the Estimation of Income Inequality Measures from Grouped Observations

[J]. Review of Economic Studies, 1976, 43, 483- 492.

[本文引用: 1]

Kakwani N , Podder N ,

On the Estimation of Lorenz Curves from Grouped Observations

[J]. International Economic Review, 1973, 14, 278- 292.

[本文引用: 2]

Kolenikov S , Shorrocks A F ,

A Decomposition Analysis of Regional Poverty in Russia

[J]. Review of Development Economics, 2005, 9, 25- 46.

[本文引用: 1]

Korinek A , Mistiaen J A , Ravallion M ,

An Econometric Method of Correcting for Unit Nonresponse Bias in Surveys

[J]. Journal of Econometrics, 2007, 136 (1): 213- 235.

[本文引用: 1]

Korinek A , Mistiaen J A , Ravallion M ,

Survey Nonresponse and the Distribution of Income

[J]. The Journal of Economic Inequality, 2006, 4 (1): 33- 55.

[本文引用: 1]

Krishnaji N ,

Characterization of the Pareto Distribution Through a Model of Underreported Incomes

[J]. Econometrica, 1970, 38 (2): 251- 255.

[本文引用: 1]

McDonald J B ,

Some Generalized Functions for the Size Distribution of Income

[J]. Econometrica, 1984, 52, 647- 663.

[本文引用: 1]

McDonald J B , Xu Y J ,

A Generalization of the Beta Distribution with Applications

[J]. Journal of Econometrics, 1995, 66 (1-2): 133- 152.

[本文引用: 2]

Menon M V ,

Estimation of the Shape and Scale Parameters of the Weibull Distribution

[J]. Technometrics, 1963, 5 (2): 175- 182.

[本文引用: 1]

Piketty T ,

Income Inequality in France, 1901-1998

[J]. Journal of Political Economy, 2003, 111 (5): 1004- 1042.

[本文引用: 1]

Pressman S ,

The Middle Class Throughout the World in the Mid-2000s

[J]. Journal of Economic Issues, 2010, 44 (1): 243- 262.

[本文引用: 1]

Sabelhaus J, Johnson D S, Ash S, Swanson D, Garner T I, et al. (2012). Is the Consumer Expenditure Survey Representative by Income?[R]. FEDS Working Papers, No. 2012/36.

[本文引用: 1]

Salem A B Z , Mount T D ,

A Convenient Descriptive Model of Income Distribution: The Gamma Density

[J]. Econometrica, 1974, 42 (6): 1115- 1127.

[本文引用: 1]

Shorrocks A, Wan G, (2009). Ungrouping Income Distributions: Synthesising Samples for Inequality and Poverty Analysis[M]//Basu K, Kanbur R. Arguments for a Better World: Essays in Honor of Amartya Sen. Oxford: Oxford University Press: 414-434.

[本文引用: 23]

Singh S K , Maddala G S ,

A Function for Size Distribution of Incomes

[J]. Econometrica, 1976, 52 (3): 647- 665.

[本文引用: 3]

Slottje D J ,

A Measure of Income Inequality in the U.S. for the Years 1952-1980 Based on the Beta Distribution of the Second Kind

[J]. Economics Letters, 1984, 15 (3-4): 369- 375.

[本文引用: 1]

Smith B E , Merceret F J ,

The Lognormal Distribution

[J]. The College Mathematics Journal, 2000, 31 (4): 259- 261.

[本文引用: 1]

Wan G ,

Understanding Regional Poverty and Inequality Trends in China: Methodological Issues and Empirical Findings

[J]. Review of Income and Wealth, 2007, 53, 25- 34.

[本文引用: 1]

/

〈 〉