网络拍卖(后者简称网拍)中的底价(reserve price), 在以往对拍卖理论的研究占了相当的地位.然而这些研究, 多聚焦于底价如何影响交易的结果(包括成交率及成交价).在理论上, 底价的功能在于平衡成交率及成交价, 因为两者之间有一个显而易见的互抵关系(trade-off): 底价设定的越高, 商品就越不容易成交, 但一旦成交, 成交价就可能越高.由于卖家的目的是在极大化预期利润(即上述两者的乘积), 因此底价的设定, 就是在平衡这两个因素¹. 本文的目的在说明底价在网拍里所扮演的理论上的角色, 其实远多于这个互抵关系.这个角色的来源, 在于eBay里的一种特别的交易方式, 叫做立即购买拍卖(auction with buy-it-now).

¹见Myerson (1981)及Riley and Samuelson (1981).

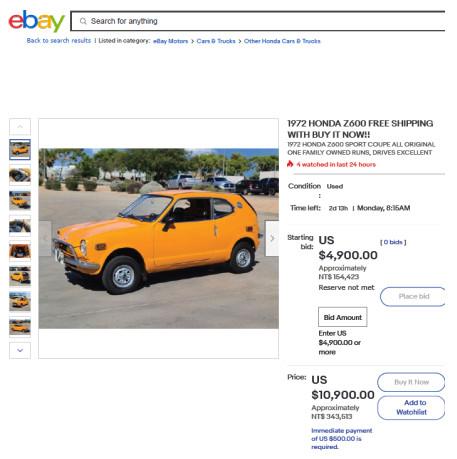
在eBay里, 当一项物品上架的时候, 卖方可以选择三种不同的上架方式.其一是一口价(posted price), 卖方直接指定上架物品的价格, 而买方只能用这个价格购买.其二是一般拍卖(regular auction).卖方对上架物品, 指定一个起标价, 在固定时间内让买方竞标决定最后价格.而起标价, 在理论上其实等同于底价.其三是立即购买拍卖(简称为BIN拍卖).这是一个eBay独有, 但为其后的各网拍所模仿的拍卖制度.物品上架时, 卖方可以设定两种价格, 一为起标价, 其功能如一般拍卖; 另一个是立即购买价(简称BIN价).在卖方所设定的立即购买价下, 买方可以在拍卖结束前的任何一个时点, 以该价格立刻结束拍卖而购买该物品, 不必再经由竞标方式. 但一旦有人下标, BIN就消失, 而变成了一个一般拍卖. 这种制度, 一方面保有拍卖的竞标精神, 另一方面又提供买方以一个固定的价格提早获得该物品的选择, 可以说是一个介于一口价和一般拍卖的混合制度². 以图 1的立即购买汽车拍卖为例, 卖方的起标价(底价)为$\$ 4,900 $, 立即购买价为$ \$10, 900 $.因为还没有人下标, 所以BIN选择还存在.一个进入网页考虑购买的买家, 可以有两种选择.第一是直接按右下方Buy it Now那个连结.这时物品就会立刻以$ \$10, 900 $的价格成交, 拍卖结束.他也可以按place bid那个连结.这时下方Buy it Now的选择就会消失, 而变成一个一般拍卖.买方这时可以在Bid Amount那一栏输入自己的投标价.至于谁得标, 就必须在拍卖结束时(由网页看是2天13小时后), 视谁是最高标决定.而成交价是第二高标³.

²这个制度是有专利的, 所以在其他的交易平台里并不存在.以中国为例, 因为网络交易量极大, 分工很细, 不同的价格决定机制, 甚至在不同的平台进行.如闲鱼是第三方上架的一口价平台, 阿里拍卖是第三方上架的一般拍卖平台.淘宝则只出售自己的商品.天猫是经认证的第三方商户的平台.每一个平台, 价格决定机制都是固定的, 没有让上架商有选择的空间.

³比如, 有三位投标者的出价分别为100, 200, 300.虽然出标300的人得标, 但成交价是200.详见第二节.

一个相当值得研究的问题是, 卖方将物品上架时, 面对这三种不同的制度, 决定他们选择其中的某一种方式来上架他的物品的主要因素是什么? 本文的第一个目的, 是提出一个卖家在这三种上架方式之间的选择的理论, 这个理论的优点, 是可以证明在卖方的选择变量是底价及立即购买价的情形下, 这三种上架方式, 其实是卖方同一个最适化问题, 在不同参数下的最适解.更重要的是, 只有这三种解.换句话说, 在卖方的选择变量是底价及立即购买价的情形下, 他只有这三种上架方式的可能性, 而且其中任何一种都有可能是某些参数值下的最适上架方式.也因此, 这个理论是卖方上架策略的一个统一(unified)的理论模型.

在这个理论下, 我们可以证明, 如卖方选择一口价上架, 其最适一口价一定高于如果他选择立即购买拍卖上架的最适底价.而后者又一定高于一般拍卖的最适底价.这个强烈的结果, 提供了一个利用eBay数据来实际检验理论的机会.本文的第二个目的, 就是利用我们所收集到的eBay iPod拍卖资料, 来验证上述理论.

理论文献里, 除了上述有关最适底价的理论外, Wang (1991)研究一口价及拍卖之间的相对优劣, 并证明当买方对物品的价值的看法较分歧时, 卖方的预期利润一般拍卖高于一口价.反之, 若较一致, 则一口价的利润较高.有关立即购买拍卖, 也有非常多理论文献, Hidvegi et al. (2006), Mathews and Katzman (2006), Reynold and Wooders (2009), Chen et al. (2013)证明了在买卖任一方是风险趋避时, 于一般拍卖之上, 再加上立即购买的选项, 可以增加卖方的预期效用(expected utility).另外, 在买卖任何一方有时间偏好(time preference)时(换句话说, 对未来收入折现时), 一般拍卖上加入立即购买的选项, 也可以增加卖方的折现利润(Mathews (2004)).

有关底价的现有文献, 几乎都在研究其对交易结果(主要是成交率及成交价)的影响.这方面的共识是底价越高, 投标人数就越少, 因此减少了成交率(例如, Reiley (2006), Choi et al. (2015), Barrymore and Raviv (2009)).其次, 给定物品成交, 成交价会随底价越高而增加(Lucking-Reiley et al. (2007)).另外, Bajari and Hortacsu (2003)的数据, 显示卖方在实际拍卖所设定的底价, 通常远比理论所得到的低.这表示物品对买方的价值, 彼此之间有较高的统计关联性(affiliated value), 或者参与拍卖有进场成本(entry cost)时, 底价的设定就要降低(Milgrom and Wilson (1982), McAfee and McMillan (1987), Levin and Smith(1994, 1996))⁴.

⁴我们并未找到与此理论相关之中文文献.但刘勇和刘树林(2020)为关键词拍卖之论文; 王明喜等(2018)为政府采购的拍卖研究; 周茜和陈收(2021)研究互联网之监管; 田婧倩等(2021)则用信息博弈研究政府之监管行为.

这一节的理论模型, 为Chen et al. (2017)的简化版, 该文利用了相当具普遍性的模型及较繁复的数理论证, 来证明本节的定理1及2.读者若希望在比较抽象的层次理解这个理论, 可以参阅该文.此处只用一个简化但相当容易了解的模型来说明.首先, 我们假设对这物品只有两个潜在买家⁵. 其次, 这物品对第$ i $个买家$ (i=1, 2) $的价值为$ v_i\in\left[0, \bar{v}\right] $, 并假设$ v_1 $和$ v_2 $为独立的变量, 但有相同的密度(density)及分配(distribution)函数$ f\left(\cdot\right) $及$ F\left(\cdot\right) $.为简化起见, 再假设$ F\left(\cdot\right) $是$ \left[0, \bar{v}\right] $上的均等(uniform)分配.且$ v_i $的值为$ i $的私人讯息(private information).

⁵事实上, 拍卖本质上就仅是最有意愿购买的前两个卖家的竞争, 其它人对拍卖结果并无影响, 所以假设仅两个潜在投标者, 完全并不影响结论的一般性.在$ n $个人的情形, 见Chen et al. (2017).

卖方在eBay将一物品上架时, 有两个变量供他选择, 一是立即购买价(后简称为BIN价) $ B $, 另一是起标价(其实就是底价) $ r $.在eBay的立即购买拍卖制度下, BIN是暂时性的.它的意思是在物品还没有人下标前, BIN这选项都会存在.但一旦有人下标了(但还没成交, 因尚未结标), 这个BIN的选项就消失, 因此这个立即购买拍卖, 就变成了一个一般拍卖⁶, 而最后获得这项物品的人就是在拍卖结束时下标最高的人.如果在尚未有人下标时, 一个潜在买家使用了这个BIN, 就表示他愿意用卖方设定的BIN价来购买这个商品.此时, 拍卖立即结束, 而物品的成交价就是$ B $.

⁶在Yahoo!的立即购买拍卖里, 不论有没有人下标, BIN的选项永远存在.所以是一个永久性的BIN.永久及暂时性的BIN, 对买卖双方的策略及拍卖结果上的差异, 见Reynold and Wooders (2009).

在网拍里, 因为拍卖时间相当长(有时多至10天), 卖方不可能在这段时间内都在在线参与竞标, 因此衍生了在一个网拍里的重要制度, 即通称的代理投标(proxy bid), 它的运作方式是, 如果在拍卖结束时最高标为$ b_i $的话, 成交价并非$ b_i $, 而是第二高标竞争者的投标价.换句话说, 得标者付的价格, 是为了打败第二高价者所需付出的最低代价.在这种情形下, 成交价$ =\{b_j|b_j\geq b_k, \forall k, j \neq i\} $.这表示在proxy bid的制度下, 网拍的价格决定方式就是在拍卖理论里通称的第二高价拍卖(second-price auction).举例来说, 假设一拍卖的起標起标价为$ \$100$.现买家$ A $进场并下标$ \$200$, 这时网页上的现有最高标(prevailing bid)就是$ \$100$ (假设投标最低增额, minimum increment, 为0).接着$ B $进场并下标$ \$150$, 这时现有最高标就变成$ \$150$ (但最高标者仍是$ A $).之后投标C进场并下标$\$300$.这时最高标买家就变成$ C $, 而现有最高标是$\$200$.接着$ D $进场, 并下标$\$250$.这时最高标变成$\$250$, 但$ C $仍为最高标买家.假如自此无人再下标, 那么拍卖结束时$ C $得标, 成交价为$\$250$.请注意这中间的价格调整完全是由机器代处理, 所以叫代理投标(proxy bid).而这个拍卖制度的最有名的一个性质, 是每位投标者标$ b_i=v_i $, 为其强势策略(dominant streategy) (例如, 见Krishna (2009)).换句话说, 一个投标者在参与网拍时, 其最适策略就是进场后, 用这样物品对自己的价值, $ v_i $, 来当作自己的投标价$ b_i $, 并离开网页让机器当作自己的代理人(proxy)下标, 一直到拍卖结束为止.这个性质, 大量减轻了在理论上计算投标策略的负担.

因为eBay的立即购买是暂时的, 所以理论上我们将立即购买拍卖看成是一个两阶段拍卖制度.第一阶段, 投标者在卖方设定的立即购买价下, 决定要不要以该价格购买.如都不愿意, 则该选择消失, 投标者进入第二阶段进行一般拍卖的竞标.如上的说明, 这等同于一个第二高价拍卖⁷. 假设卖方的折现因子为$ \delta\in[0, 1] $.换句话说, 买卖方在第二阶段的收入若为$ x $, 其在第一阶段的折现则为$ \delta x $.在这情形下, 立即购买的好处就显现出来. 由于买方并无折现, 因此他愿意在第一期以$ B $的价格购买的原因, 并不在第二期会有折现, 而是希望避免在第二期和其他对手竞争. 也因此, 通常卖方会用稍低于如果用定价出售的价格来诱使买方第一阶段启用立即购买. 当然, 对卖方而言, 这个好处来自于避免第二阶段才成交的折现. 因此卖方的立即购买价的值, 是在这两种考虑之下而决定.

⁷这是研究暂时性立即购买拍卖的标准理论模型, 见Reynold and Wooders (2009), Mathews and Katzman (2006), 及Mathews (2004).

由于BIN拍卖是一个投标者之间的两阶段博弈, 因此我们利用回朔法(backward induction)求解.在第二阶段的一般拍卖里, 假设投标者$ i $的投标策略函数是$ b_i\left(v\right) $, 换句话说, 物品如果对它的价值为$ v $时, 他用$ b_i\left(v\right) $的值来投标.我们已经说明过, 由于拍卖等同于第二高价拍卖, 因此买方的最适投标策略就是$ b_i\left(v\right)=v $⁸, 在这个策略下其预期利润为:

⁸当然, 我们假设$ i $的$ v $值大于$ r $, 否则他根本不会参与投标.

$ \begin{equation*} {\rm Eu}_A\left(v\right)=\int_{0}^{r}\left(v-r\right)f\left(x\right){\rm d}x+\int_{r}^{\bar{v}}{\left(v-x\right)f\left(x\right){\rm d}x.} \end{equation*} $

上式的第一项, 是这个买家(物品对他之价值为$ v $)的对手(物品对其价值为$ x $), 其$ x $值在$ r $之下, 所以买家以$ r $得标.第二项是对手的物品价值$ (x) $低于自己, 因而得标(并付第二高价$ x $)的预期利润.据此, 我们回到第一阶段立即购买阶段.由于$ v $值越高, 该投标者用$ B $购买的利润越高, 而且当$ v $够小的时候.该投标者用$ B $来购买的利润就越小, 甚至变成负数⁹. 因此, 存在一个门坎值$ \widetilde{v}\in\left(0, \bar{v}\right) $, 使得物品对投标者的价值$ v>\widetilde{v} $时, 他会在第一阶段用$ B $购买.否则他会等待到第二阶段竞标¹⁰. 在这个门坎策略下, 物品对其价值为$ v $的投标者, 其预期利润为:

⁹例如, 当以$ B $时, 立即购买一定不值得.

¹⁰这也是eBay立即购买拍卖的基本理论模型.见Mathews and Katzman (2006), Reynold and Wooders (2009), 及Chen et al. (2013).

$ \begin{equation*} {\rm Eu}_B\left(v\right)=F\left(\widetilde{v}\right)\left(v-B\right)+\frac{1}{2}\left[1-F\left(\widetilde{v}\right)\right]\left(v-B\right)=\frac{\left(\bar{v}+\widetilde{v}\right)\left(v-B\right)}{2\bar{v}}. \end{equation*} $

在上式中, 第一个等号后的第一项为对手的$ v $值小于$ \widetilde{v} $ (其机率为$ F\left(\widetilde{v}\right) $).因此该投标者为唯一用$ B $购买者.第二项是如果对手的价值也大于$ \widetilde{v} $ (其机率为$ 1-F\left(\widetilde{v}\right) $), 两人都愿用$ B $来购买.此时假设每一投标者获得的机率相等.

最后, 门坎值$ \widetilde{v} $的决定等式, 当然是让第一阶段直接购买的利润和等到第二阶段才目标利润相等.换言之, $ {\rm Eu}_B\left(\widetilde{v}\right)={\rm Eu}_A\left(\widetilde{v}\right) $.由此, $ \widetilde{v} $必然满足:

(1) $ \begin{equation} B=\widetilde{v}-\frac{{\widetilde{v}}^2-r^2}{\bar{v}+\widetilde{v}}. \end{equation} $

值得注意的是, 当$ \widetilde{v} $和$ r $固定的时候, 由(1)式所定义出来的$ B $值, 其实就是为了让立即购买的门坎值为$ \widetilde{v} $, 所必须设定的立即购买价.因此, 我们将(1)式的右式写为$ B\left(\widetilde{v}, r\right) $, 用以表示如果卖方希望门坎值为$ \widetilde{v} $, 所应该设的BIN价.请注意$ B(\widetilde{v}, r) $是$ \widetilde{v} $的严格递增函数, 所以两者为1-1对应.也因此, 卖方的决策变量(decision variable)虽为$ B $和$ r $, 但其实等同于选择$ \widetilde{v} $和$ r $.由于eBay的规定$ B $必须大于$ r $¹¹, 因此我们必找到相对于$ \widetilde{v} $的限制.引理1给了答案.

¹¹这其实很自然.如果起标价还比立即购买价高, 那么这制度自相矛盾.

引理1  令$ B $和$ \widetilde{v} $满足(1)式.则$ B>r $若且唯若$ \widetilde{v}>r $.且$ B=r $同等于$ \widetilde{v}=r $.

证明  如果$ B>r $, 但$ \widetilde{v}<B $的话, 那么由于$ B $严格递增于$ \widetilde{v} $, 可知$ B=B(\widetilde{v}, r)<B(B, r)\leq B $.这是一个矛盾.反之, 若$ \widetilde{v}>r $, 那么$ B=B(\widetilde{v}, r)\geq B(r, r)=r $.最后, 如果$ B=r $, 那么表示$ B=B(B, r) $, 这即表示$ B=\widetilde{v} $, 但这一等式仅在$ \widetilde{v}=r $时才会成立.

根据引理1, 我们可以将卖方的最适化问题改写为:

$ \begin{equation*} \begin{aligned} \underset{\widetilde{v}, r}{\max} E \pi \left(\widetilde{v}, r \right)= &2 \int_{\widetilde{v}}^{\bar{v}} B\left(\widetilde{v}, r \right) F\left(x \right) f\left(x \right){\rm d}x+ \\ & \delta \left[ 2\int_{r}^{\widetilde{v}}\left(\int_{r}^{x}y{\rm d}F\left(y\right)+\int_{0}^{r}r{\rm d}F\left(y\right)\right)f\left(x\right){\rm d}x \right], \\ \mbox{s.t. } \widetilde{v} &\geq r. \end{aligned} \end{equation*} $

这个模型的最重要观察, 就是三种上架方式的决定性因素, 在于上述最大化问题在某些情形下会有角解(corner solution).如果它的解是让$ B=r $, 表示起标价和立即购买价相等.这时这个物品其实就等于是用定价$ B $ (或$ r $)出售, 因为任何一个买方, 如愿意下标, 他的下标价至少要是$ r $, 然而$ B=r $, 且他用$ B $就可以立即买到, 无需等到第二阶段下标.因此这物品事实上是定价为$ B $的一口价.其次, 如果上面最适化问题的解$ \widetilde{v} $和$ r $, 让$ B\left(\widetilde{v}, r\right)\leq B $, 那么表示即便对这物品有最高价值的投标者(即$ v=\bar{v} $), 都不愿意在第一阶段用立即购买价来购买¹². 因此, 卖方的最适解如果是让$ B\left(\bar{v}, r\right)\leq B $, 表示他根本不想让人用立即购买价去买这物品, 因此这时上架方式就等同于一个一般的拍卖.最后, 如果上面的最适化问题的解有内解(interior solution), 即$ r<B<B\left(\bar{v}, r\right) $, 那么这个上架方式就是一个立即购买拍卖.也因此, 我们的理论模型完全刻划(completely characterize)了eBay上可以见到的三种上架方式¹³. 也就是说, 我们的理论可以将卖方的各上架策略内生化(endogenize)¹⁴.

¹²$ B\left(\bar{v}, r\right) $是为了让物品价值为$ \bar{v} $的投标者愿意用$ B $购买的最高门坎.由于没有一个投标者的$ v $值会高于$ \bar{v} $, 而价值最高的买方的愿付最高BIN价, $ B\left(\bar{v}, r\right) $, 都还比$ B $小, 表示没有人会在第一阶段用$ B $购买.

¹³eBay上还有一种上架方式叫best-offer.这基本上是一个利用讨价还价的方式来决定价格的机制, 这和上述三种机制完全不同.

¹⁴完整的理论, 请见Chen et al. (2017), 在这个架构下的实证研究, 见Chen et al. (2018).

在上述的刻画方式下, 我们接下来要研究的, 就剩下在什么情形下, 卖方的最适化问题会有角解(以及何种角解), 以及何时会有内解.我们先将这最适化问题改写为:

(2) $ \begin{equation} \underset{\widetilde{v}, r, \lambda}{\max} L= \left[\frac{{\bar{v}}^2-{\widetilde{v}}^2}{{\bar{v}}^2}\right]\left[\frac{\bar{v}\widetilde{v}+r^2}{v+\widetilde{v}}\right] +\frac{\delta}{{\bar{v}}^2}\left[\frac{1}{3}+r^2\widetilde{v}-\frac{4}{3}r^3\right] +\lambda\left(\widetilde{v}-r\right), \end{equation} $

其中$ \lambda \geq 0 $为拉氏乘数(Lagrange multiplier).其一阶条件为:

(3) $ \begin{equation} \begin{aligned} &\frac{\partial L}{\partial \widetilde{v}}= 1-2\frac{\widetilde{v}}{\bar{v}}+\delta\frac{{\widetilde{v}}^2}{{\bar{v}}^2}+\left(\delta-1\right)\frac{r^2}{{\bar{v}}^2}+\lambda=0, \\ &\frac{\partial L}{\partial r}= \frac{2\delta r}{{\bar{v}}^2}\left[\bar{v}-2r+ \left(\bar{v}-\widetilde{v}\right) \left(\frac{1}{\delta}-1 \right) \right]-\lambda=0, \\ &\lambda\left(\widetilde{v}-r\right)=0. \end{aligned} \end{equation} $

我们分开讨论两种情形, 即$ \widetilde{v}\geq r $这个限制式是否等式成立(binding); 如是, 则$ \lambda>0 $, 如否, 则$ \lambda=0 $.

当$ \lambda>0 $时, 根据引理1, 这是一口价上架.由一阶条件可以很容易解出:

$ \begin{equation*} \begin{aligned} \widetilde{v} &= r=\bar{v} / \sqrt{3} \equiv r_F, \mbox{且}\\ \lambda &= \frac{2}{3}(\sqrt{3} - 1 - \delta). \end{aligned} \end{equation*} $

值得注意的是, $ r_F $的值和$ \delta $无关.这个原因很明显: 如果买方愿意用固定价格购买, 那么一定在第一阶段就买, 不会等到第二阶段还损失折现.此时卖家的利润为$ \pi_F^\ast=2\sqrt3\bar{v}/q $.这其实就是卖方直接用定价出售的最适定价: 假设卖家定价$ p $, 那他预期利润为$ [ 1-F \left(p)^2 \right]p $¹⁵. 最适定价可以很容易解出为$ p^* =\bar{v} / \sqrt{3} $, 这即上面的最适$ r $ (及$ \widetilde{v} $)值.由于$ \lambda\geq0 $, 因此$ r=\widetilde{v} $唯有在$ \delta \leq \sqrt{3} -1 \equiv \hat{\delta} $时才会是最适解.

¹⁵$ 1-F\left(p\right)^2 $为至少有一买家的$ v $值大于$ p $的机率.

第二种情形, 为$ \lambda=0 $ (即$ \widetilde{v}>r $).这时可以很容易地解出:

(4) $ \begin{align} \widetilde{v} \left(\delta \right) &= \frac{\left(1- 2\delta- 3\delta^2 \right)+ 2 \delta \sqrt{-1+2\delta+4\delta^2-5\delta^3}}{1-3\delta+3\delta^2-5\delta^3}\bar{v}, \end{align} $

(5) $ \begin{align} r \left(\delta \right) &= \frac{ 2 \delta \left(2\delta-1 \right)+ \left(1-\delta \right) \sqrt{-1+2\delta+4\delta^2-5\delta^3}}{-1+3\delta-3\delta^2+5\delta^3}\bar{v}. \end{align} $

由(4)和(5)式可以很容易看出$ r $和$ \widetilde{v} $的最适值, 都和$ \delta $有关.这时卖家的预期利润为:

(6) $ \begin{equation} \pi_B^*= \frac{ [ 4 (-1+\delta+5\delta^2) \sqrt{(\delta-1)^3(1-\delta-5\delta^2)} -2+ 21\delta-51\delta^2+7\delta^3+45\delta^4 ]} { 3(1-3\delta+3\delta^2-5\delta^3)^2} \delta\bar{v}. \end{equation} $

卖方用一口价上架的预期利润, $ \pi_B^* $, 的重要性质, 是它为$ \delta $的递增函数.换句话说, 当卖方越有时间耐性的时候, 就越有筹码可以策略性的选择$ r $和$ \widetilde{v} $, 让自己的利润较大, 另外, $ \pi_F^*\geq \pi_B^* $若且唯若$ \delta<\hat{\delta} $, 且两者在$ \delta=\hat{\delta} $时相等.由于$ \pi_B^* $递增于$ \delta $而$ \pi_F^* $和$ \delta $无关, 我们立刻可以知道当$ \delta\in (0, \hat{\delta} ] $时, 卖方的最适上架方式就是一口价.

最后, 由(4)式可知$ \widetilde{v}(1)=\bar{v} $, 表示当$ \delta=1 $时, 卖方会将$ \widetilde{v} $设在没有任何买家会立即购买的值.换句话说, 如果卖方对利润没有任何折现($ \delta=1 $), 那么其最适上架方式就是一般拍卖, 而由(5)式, 此时的最适价格是$ r(1)=\bar{v} / 2\equiv r_A $.就此, 我们得到以下定理:

定理1  当$ \delta=1 $时, 卖方的最适上架方式为一般拍卖.若$ \delta \in (0, \hat{\delta} ] $, 其最适上架方式为定价出售.若$ \delta \in (\hat{\delta}, 1) $, 其最适上架方式为立即购买拍卖.

定理1的刻划核心, 在于上架方式的选择, 完全由卖方的时间偏好决定.对未来折现最大的卖家$ (\delta \leq \hat{\delta}) $, 会希望早点将物品卖出去, 因此会用一个较低的定价(请注意, 在我们的模型里, 这就是角解的底价)让物品在第一阶段就卖出.折现程度中等的卖家(即$ \hat{\delta}<\delta<1 $), 则是平衡及搭配一口价和一般拍卖的优点, 而利用立即购买拍卖, 使物品有机会让物品由立即购买价(如果有一买家的$ v $值较大)或拍卖(如果两个买家的$ v $值都较小)卖出.最后, 如果他对未来毫无折现($ \delta=1 $), 那么最好的上架方式, 就是让两个买家在第二阶段经由竞争来决定价格.虽然这是对卖方的最适上架策略的相当美妙的刻画, 但本文最主要的目的是最适底价的比较.下面的定理2, 说明卖家如何利用底价的设定达到上述目的.

定理2  $ r_F>r_B (\delta) > r_A, \forall\delta\in(\hat{\delta}, 1) $, 且$ r_B(r) $为$ r $之递减函数.

证明  由(3)式我们知道当$ \delta\in(\hat{\delta}, 1) $时,

$ \begin{equation*} \begin{aligned} r_B\left(\delta\right) &= \frac{\bar{v}}{2}+\frac{\bar{v}-\widetilde{v}\left(\delta\right)}{2}\left(\frac{1}{\delta}-1\right)\\ &> \frac{\bar{v}}{2}=r_A. \end{aligned} \end{equation*} $

我们也知道在立即购买拍卖中, $ \widetilde{v} \left(\delta \right)>r \left(\delta \right) $, 因此,

$ \begin{equation*} \begin{aligned} r_B\left(\delta\right) &= \frac{\bar{v}}{2}+\frac{\bar{v}-\widetilde{v}\left(\delta\right)}{2}\left(\frac{1}{\delta}-1\right)\\ &< \frac{\bar{v}}{2} + \frac{\bar{v}-r\left(\delta\right)}{2}\left(\frac{1}{\delta}-1\right). \end{aligned} \end{equation*} $

这表示,

$ \begin{equation*} r_B\left(\delta\right)<\frac{\bar{v}}{1+\delta}<\frac{\bar{v}}{1+\hat{\delta}}=\frac{\bar{v}}{\sqrt3}=r_F. \end{equation*} $

上面第二个不等式, 来自于在使用立即购买拍卖的卖家, 其$ \delta > \hat{\delta} $. 最后, $ r_B(\delta) $很明显是$ r $的递减函数.

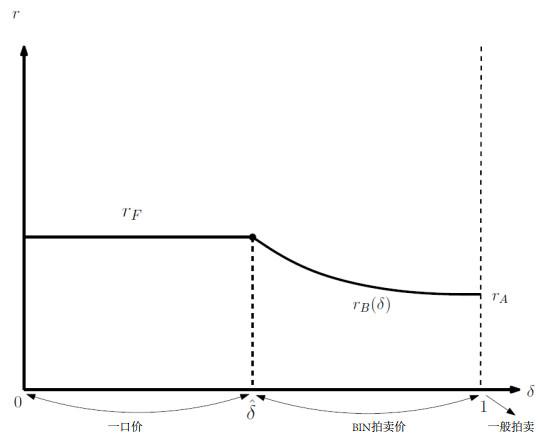
从图 2很清楚地归纳了定理1和2的内容, 该图横轴$ \delta $由0到1.横轴上我们注记了在哪些区域里, 哪一种上架方式让卖方的预期利润最大, 纵轴对应于该$ \delta $值(以及其最适的上架方式)的最适底价.图的一件观察, 是当$ \delta \in (\hat{\delta}, 1) $时, 虽然卖方都使用立即购买拍卖, 但在不同的$ \delta $值下, 有不同的底价.然而, 更重要的是, $ r_B\left(\delta \right) $是$ \delta $的递减函数.这表示当卖方越有耐性, 就越愿意让买方低价起标而进入第二阶段的竞价拍卖.

这个结果也同时说明了底价的大小, 不但在三种上架方式上有固定的排序, 连相对的$ \delta $值都有固定排序.要而言之, 底价在整个$ \left[0, 1\right] $之间都是$ \delta $的递减函数.

定理2提供了一个清楚的实证规律, 假如我们在eBay上收集用不同的方式上架的相同物品, 一定要发现一口价一定高于立即购买拍卖的底价, 而后者一定又高于一般拍卖的底价.本文的第二部分, 就是希望证实这件事.

我们使用的数据, 来自2007年11月1日到12月31日, 在eBay上的iPod Nano拍卖¹⁶. 资料的收集首先遇到的最大问题, 是eBay的立即购买是暂时的, 一旦有人下标, 立即购买就消失.因此, 当我们用爬虫收集到一个拍卖正在进行中的商品时, 并不表示它原是用一般拍卖上架的.它可能原先是一个立即购买拍卖, 但因为结束前有人下标了, 所以变成了一个一般拍卖. 因此, 任何一个物品, 我们都必须在它一上架的时候, 立刻开始记录它的交易过程, 一直到它结束为止.也因为如此, 在收集过程中, 我们让计算机连续跑了两个月.

¹⁶iPod是早期Apple专门用来让消费者购买、储存及听音乐的装置.这个装置因为手机功能的大幅跃进, 现在已被淘汰.

为了让物品的同构型较高, 以避免因物品本身的差异而产生不同, 数据仅包含Nano 4G第三代的iPod.另外有些上架的iPod设有秘密底价, 也有些物品的底价高得离谱(比如$ \$1, 595 $), 这些样本都删除.最后的数据里共有$ 1, 186 $个iPod, 这之中有$ 928 (78%) $是一般拍卖上架, $ 80 (6.7%) $是立即购买拍卖, $ 178 (15.3%) $是一口价.一般拍卖的成交率是$ 94.83% $, 立即购买拍卖为71.25%, 而一口价是$ 82.58% $.这么高的成交率, 表示当时iPod是相当抢手的商品.表 1为三种上架物品的叙述统计.

数据里也包含了物品及卖方的信息, 前者包括底价(RP), 上架时间长度(DURATION), 运费(SHIPCOST), 物品是否可退货(RETURN, 是为1).后者包括卖方曾交易的物品总数(EXPER, 也就是他的经验值), 卖方所获正评价占总评价的比例(POSFB), 及存货数(INVENTORY), 其定义为卖方在该物品上架时, 手中有的iPod数目.有关上述变量的叙述统计在表 2及表 3.

在这一节里, 我们做了两个实证研究, 两者都是验证定理2.该定理其实包括两个结果, 第一是一口价大于立即购买拍卖的底价, 而后者又高于一般拍卖的底价.第二是底价和$ \delta $的值有反向关系.

在做这之前, 有一件困难必须先解决.在数据里, 有相当数目的物品, 其底价非常低¹⁷. 如前所述, 理论文献对低底价有两种解释.第一是, 当各买方对物品的价值之间, 有统计相关性(affiliated)时, 每一次投标, 都会对其他投标者揭露出有用的讯息出来.当没有人投标时, 由于讯息不对称, 大家都保守下标, 怕下标太高赔钱. 为了鼓励讯息揭露, 卖方就会以低价起标, 以揭露出更多的讯息(Milgrom and Weber (1982)).

¹⁷以$\$0.01 $、$\$0.25$、$\$0.5$、$\$0.88$、$\$0.99$、$\$1$为底价之物品的数目(及比例)分别为244(24%)、4(0.4%)、3(0.3%)、332(32%)及63(6.25%), 占总上架数的68%.这现象不只在我们的数据中, 也在其他数据出现(例如, Bajari and Hortacsu (2003).

另一个解释是进场成本.假设投标者要进场之后才能知道物品对他们的价值, 当进场投标需要成本的时候, 由于底价越高会让成交价越高, 且进场成本是固定的, 所以底价越高, 进场后所得到的净利就越小, 甚至是负的.这就越阻止买方进场, 从而降低了卖方可能的利润.为了让更多人进场竞价, 卖方也会以低价起标(McAfee and McMillan (1987), Levin and Smith(1991, 1996)).

由于低底价起标, 是卖方的内生选择(endogenous decision), 我们决定用工具变量(instrumental variable)的方式来内生这个选择, 我们使用的方式是以底价为被解释变量, 但为一截断变量(censored variable).主要原因是卖方在物品上价时, eBay规定他们必须设定一个起标价(即底价), 而最低容许的起标价为$\$0.01$, 所以将底价设为$\$0.01$的卖家, 其实就是根本没有设底价的人, 也等于是被截断的样本.根据这个推论, 我们把截断值设在$\$0.01$做一个标准的截断回归(censored regression).另外, 由于上架方式也是内生的, 所以我们用一个多元(multinomial) probit模型来内生化卖方会选择用何种上架方式.这两个设定结合, 让回归式成为一典型的mixed-process模型(Roodman (2011)).

至于定理2第二个结果的实证, 我们利用存货量当作$ \delta $值的工具变数, 来验证底价与$ \delta $之间的反向关联.

考虑如下的截断回归:

(7) $ \begin{equation} {\rm RP}=\alpha_0+\alpha_1 {\rm BIN}+\alpha_2 {\rm FP}+\alpha_3 X+\epsilon_1. \end{equation} $

BIN及FP各自为BIN拍卖和一口价的虚拟变量(dummy variable), $ X $是所有可能会影响底价RP的因素, 包括运费(SHIPCOST), 正评价比例(POSFB), 及是否商品可退回(RETURN) ¹⁸. $ \alpha_1 $及$ \alpha_2 $的值是我们的主要兴趣.如果定理1是正确的话, 那么应该$ \alpha_2>\alpha_1>0 $.

¹⁸我们没有考虑卖方固定效果(fixed effect), 因为在432个卖家里, 有302个只交易一次.所以我们只用卖方特性(如POSFB)来控制.

如前所言, BIN及FP的选择是内生的, 因此我们用了多元probit来估计卖方所选择使用的上架方式, 将(7)式用截断回归来估计.为了这个目的, 我们用卖方所自行设定的上架时间(DURATION)为exclusive变量¹⁹. (7)式因此变成了一个mixed-process.我们用最大概似法(maximum likelihood method)来估计.假设$ \epsilon_1 $的变异数(variance)为1, 则样本选择式(selection equation)的变异数就是相对变异量(relative variance)的解, 而(7)式就可以用共变异量(covariance)的估计来认定(identified).估计的细节请见附录A.

¹⁹成交率应和DURATION成正比, 也因此卖方在将DURATION设较大的时候, 就较不会低价起标.我们会将DURATION放入(7)式当作解释变量, 发现其系数并不显著(见表 4和5).这表示DURATION是合理的exclusive变量.

估计结果列于表 4.由该表可看出, 卖家选择用立即购买拍卖的可能性, 和其经验成反比(5%显著).而存货量(INVENTORY)和选择用一口价的可能性呈正向关系. DURATION的系数显著为正, 表示如果卖方上架时间选择的较长, 就设越高的底价.我们的主要兴趣在$ \alpha_1 $及$ \alpha_2 $的值.由表可看出$ \alpha_1=125.4 $, $ \alpha_2=155.4 $ (两者都在1%显著).这很清楚证实了三种上架方式的底价排序.

表 4的一些其它结果也值得我们注意.首先, 卖方的经验和它使用立即购买拍卖上架的倾向成反比.这和Chen et al. (2013a, 2013b)的结果相符合.该文也证实了卖方经验是决定它是否则用立即购买上架的重要因素.在文献里, BIN扮演了减低拍卖价格风险的角色(见Hidvegi et al. (2006), Mathews and Katzman (2006), Reynolds and Wooders (2009), Chen et al. (2013)).一个经验越少的卖家, 越需要BIN来帮助它减低上架的价格风险.其次, 存货量显著和选择一口价上架有正相关, 这和Chen et al. (2018), Hammond (2010)的结论是相同的²⁰. 它的理由其实非常直觉: 在2007年时, 在eBay上还没有办法在一般或立即购买拍卖的同一个网页里上架多个相同物品.而一口价则对此非常方便.比如说, 假如卖家有18个iPod要出售, 与其用了较高的成本以18个网页用拍卖上架, 不如将这18个物品用一个固定的一口价全部一起上架, 一直到卖完为止.这节省非常多的人力成本.

²⁰请注意Hammond (2010)对存货量的定义和本文稍有不同.

定理2证明了底价和折现因子(discount factor) $ \delta $之间的反向关系.然而后者在现实上是观察不到的, 所以必须求助于替代变量(proxy).这个变量就是存货量.一个存货量高的卖家, 我们可以想象应该比较有存货成本及压力, 也代表它比较希望早点将物品售出.也因此, 他应有较高的折现.换句话说, 一个卖家的存货量应该和它的折现因子的大小成反比.这又表示如果定理2是正确的话, 存货量应该和底价成正比.当然, 上一小节所谈的底价截断现象仍然存在.我们利用Heckman回归来当作实证模型.首先将样本分为两部分, 第一部分是将底价设为$ \$0.01$的样本, 另一个是大于$ \$0.01$的.因此, 样本选择(sample selection)的标准是底价是否为$ \$0.01$²¹. 值得注意的是一旦我们用存货量当作替代变量, 它和折现因子的正向关系就应独立于卖方是用三种方式的哪一种上架, 也因此, 在(7)式中的BIN及FP虚拟变量就不再需要²².

²¹为了了解Heckman回归结果的稳健性(robustness), 我们也用了最大概似法来估计, 其结果一致, 见http://idv.sinica.edu.tw/kongpin/WebAddpendix7.pdf.

²²细节请见附录B.

表 5的样本选择式(selection equation)显示, 较有经验, 运费要求较低, 及正评比例较低的卖家, 较容易将底价设在$ \$0.01$更重要的是, 存货量较大的卖家, 较有可能将底价设在$ \$0.01$最后样本选择式和主回归式的残差项及相关系数(correlation) $ \rho $, 显著不等于0, 表示样本选择偏差(selection bias)存在, 所以使用Heckman回归是必需的. 表 5的上方清楚显示(1%显著水平)了存货量和底价的正向关系, 再由样本选择式的回归结果, 我们证实了底价和折现因子的反向关系.

这篇论文首先提出了一个理论模型, 将网拍理卖方的三种上架策略, 经由他们的时间偏好完全刻划出来.一个对未来无折现的卖家, 将会使用一般拍卖将物品上架, 而对未来折现最多的, 会选择一口价.中间的卖方, 则使用立即购买拍卖.这个理论的副产品, 是三种上架方式所设的底价(在理论里, 一口价的定价是角解条件下的底价), 有一个固定的排序, 而这个排序是可以用数据来验证的.我们利用eBay的iPod上架数据来证实这个排序, 另外, 本文也发现卖方的存货量和其对未来的折现有强烈关联.利用这个关联为桥梁, 我们证实了里论中, 折现因子和底价之间的反向关联.

这个附录简单的说明4.1节mixed-process模型.为了方便起见, $y_1 $代表RP, $x_1=\left({\rm BIN, FP}, X \right) $是(7)式的解释变量, 即(A1)及(A2)式里的x. (A2)是RP的样本选择式(selection equation), 因为在截断回归里, y₁>0.01仅在y₂>0时.令y₃=0, 1, 2.代表这三种上架方式.其mixed-process模型为:

(A1) $y_1=x_1^T \beta_1+\epsilon_1, $

(A2) $y_2=x_2^T \beta_2+\epsilon_2, $

(A3) $y_3=j, \quad \text { if } \quad v_j=\max \left\{v_0, v_1, v_2\right\}.$

(A3) 式里的y₁所对应的值函数(value function) 为:

(A4) $\begin{aligned}& v_0=0, \\& v_1=z^T r_1+\epsilon_3, \end{aligned}$

(A5) $v_2=z^T r_2+\epsilon_4.$

y₃= 1和2分别段应于BIN和FP, 而y₃= 0代表参考点(即一般拍卖), 其值我们设为0. 为了用最大概似来估计(A1)~(A5) 式, 我们假设残差项为多元常态分配:

$\left(\begin{array}{l}\epsilon_1 \\\epsilon_2 \\\epsilon_3 \\\epsilon_4\end{array}\right) \sim N_4\left(\left(\begin{array}{l}0 \\0 \\0 \\0\end{array}\right), \left(\begin{array}{cccc}\sigma_1^2 & \rho_{12} \sigma_1 & \rho_{13} \sigma_1 \sigma_4 & \rho_{14} \sigma_1 \sigma_4 \\\rho_{12} \sigma_1 & 1 & \rho_{23} \sigma_4 & \rho_{24} \sigma_4 \\\rho_{12} \sigma_1 \sigma_3 & \rho_{23} \sigma_4 & \sigma_4^2 & \rho_{34} \sigma_4^2 \\\rho_{12} \sigma_1 \sigma_4 & \rho_{24} \sigma_4 & \rho_{34} \sigma_4^2 & \sigma_4^2\end{array}\right)\right) \text {. }$

在这个mixed-process模型里, (A1)~(A2) 式是Heckman’s样本选择式(sample selection), 而(A3)~(A5) 式则为多元(multinomial) probit模型, 其边际机率(marginal probabilities) 在y₃ = 0, 1和2时分别为:

$\begin{aligned}& Pr\left(y_3=0\right)=Pr\left(v_0>v_1, v_0>v_2\right)=Pr\left(\left(\begin{array}{c}\epsilon_3 \\\epsilon_4\end{array}\right)<\left(\begin{array}{c}-z^T r_1 \\-z^T r_2\end{array}\right)\right), \\& Pr\left(y_3=1\right)=Pr\left(v_1>v_0, v_1>v_2\right)=Pr\left(\left(\begin{array}{c}\epsilon_3 \\\epsilon_3-\epsilon_4\end{array}\right)<\left(\begin{array}{c}z^T r_1 \\z^T r_1-z^T r_2\end{array}\right)\right), \\& Pr\left(y_3=2\right)=Pr\left(v_2>v_0, v_2>v_1\right)=Pr\left(\left(\begin{array}{c}\epsilon_4 \\\epsilon_4-\epsilon_3\end{array}\right)<\left(\begin{array}{c}z^T r_2 \\z^T r_2-z^T r_1\end{array}\right)\right).\end{aligned}$

令1(·) 为indicator函数, 且$\theta=\left(\beta_1^T, \beta_2^T, \gamma_1^T, \gamma_2^T, \sigma_1, \sigma_4, \rho_{12}, \rho_{13}, \rho_{14}, \rho_{23}, \rho_{24}, \rho_{34}\right)^T $为mixedprocess模型的所有参数. 再令$y_{2 i}=1\left(y_{2 i}^*>0\right) $, 其log-likelihood函数则为:

$\begin{aligned}\ln L(\theta)= & \sum\limits_{i=1}^n \ln f\left(y_{1 i}, y_{2 i}, y_{3 i} \mid x_{1 i}, x_{2 i}, z_i ; \theta\right) \\= & \sum\limits_{i=1}^n\left\{\ln f\left(\epsilon_{1 i}, \epsilon_{2 i}>-x_{2 i}^T \beta, v_{0 i}>v_{1 i}, v_{0 i}>v_{2 i}\right) \cdot 1\left(y_{2 i}=1, y_{3 i}=0\right)+\right. \\& \ln f\left(\epsilon_{1 i}, \epsilon_{2 i}>-x_{2 i}^T \beta, v_{1 i}>v_{0 i}, v_{1 i}>v_{2 i}\right) \cdot 1\left(y_{2 i}=1, y_{3 i}=1\right)+ \\& \ln f\left(\epsilon_{1 i}, \epsilon_{2 i}>-x_{2 i}^T \beta, v_{2 i}>v_{0 i}, v_{2 i}>v_{0 i}\right) \cdot 1\left(y_{2 i}=1, y_{3 i}=2\right)+ \\& \ln f\left(\epsilon_{2 i} \leq-x_{2 i}^T \beta, v_{0 i}>v_{1 i}, v_{0 i}>v_{2 i}\right) \cdot 1\left(y_{2 i}=0, y_{3 i}=0\right)+ \\& \ln f\left(\epsilon_{2 i} \leq-x_{2 i}^T \beta, v_{1 i}>v_{0 i}, v_{1 i}>v_{2 i}\right) \cdot 1\left(y_{2 i}=0, y_{3 i}=1\right)+ \\& \left.\ln f\left(\epsilon_{2 i} \leq-x_{2 i}^T \beta, v_{2 i}>v_{0 i}, v_{2 i}>v_{1 i}\right) \cdot 1\left(y_{2 i}=0, y_{3 i}=2\right)\right\}.\end{aligned}$

最后, 上式θ的最大概似估计量(maximum likelihood estimator)为:

$\theta=\arg \max\limits _{\theta \in} \ln L(\theta).$

这个附录里, 我们简单的说明4.2节所使用的样本选择式(sample selection)模型.令y代表RP, x₃为主要回归式的解释变量, $x_4=\left(x_3, \mathrm{POSTDUR}\right) $为样本选择式的解释变量, 其中$y_s=0 $为底价被截断, $y_s=1 $为未截断. x=SHIPCOST, POSFB, RETURN和4.1节同.回归式模型如下

(B1) $y = \left\{ {\begin{array}{*{20}{c}} {{x_3}\theta + u{\text{若 }}{y_s} = 1\;\;\;{\text{ i}}{\text{.e}}{\text{. }}y > 0.01{\text{, }}} \\ {0.01{\text{ 若 }}{y_s} = 0\,\,\,{\text{ i}}{\text{.e}}{\text{. }}y > 0.01.{\text{ }}} \end{array}} \right.$

(B2) $y_s= \begin{cases}1 & \text { 若 } y_s^*>0, \\ 0 & \text { 若 } y_s^* \leq 0 .\end{cases}$

(B3) $y_s^*=x_4 \theta_s+u_s \text {. }$

为了使用Heckman两阶段估计, 假设(B1)~(B2) 式残差项为双元常态分配.

$\left(\begin{array}{c}u \\u_s\end{array}\right) \sim N_2\left(\left(\begin{array}{l}0 \\0\end{array}\right), \left(\begin{array}{cc}\sigma^2 & \rho \sigma \\\rho \sigma & 1\end{array}\right)\right).$