中国科学院数学与系统科学研究院期刊网

计量经济学报, 2022, 2(2): 237-256 DOI: 10.12012/CJoE2021-0069

 

基于CNN与LSTM多组合策略的中国碳市场价格预测

陈晓红,1,2, 龚思远,1, 贺怡帆,1, 曹文治,1,2, 刘厚盾,1

1. 湖南工商大学前沿交叉学院, 长沙 510275

2. 中南大学商学院, 长沙 510280

Carbon Price Forecasting in Chinese Carbon Trading Market Based on Multi-Strategy CNN-LSTM

CHEN Xiaohong,1,2, GONG Siyuan,1, HE Yifan,1, CAO Wenzhi,1,2, LIU Houdun,1

1. School of Frontier Crossover Studies, Hunan University of Technology and Business, Changsha 510275, China

2. School of Business, Central South University, Changsha 510280, China

通讯作者: 曹文治, 副教授, 博士, 研究方向: 大数据分析技术与应用, E-mail:2652@hnuc.edu.cn

收稿日期: 2021-09-13  

基金资助: 国家自然科学基金委基础科学中心项目.  72088101
国家自然科学基金重大研究计划集成项目.  91846301
湖南省研究生科研创新项目.  CX20211113

Received: 2021-09-13  

Fund supported: National Natural Science Foundation of China.  72088101
National Natural Science Foundation of China.  91846301
Postgraduate Research and Innovation Project of Hunan Province.  CX20211113

作者简介 About authors

陈晓红,中国工程院院士,教授,博士生导师,研究方向:两型社会与生态文明、大数据分析技术与应用、决策理论与方法,E-mail:c88877803@163.com

龚思远,硕士研究生,研究方向:两型社会与碳排放分析,E-mail:gsyuan28@163.com

贺怡帆,硕士研究生,研究方向:能源与环境分析,E-mail:heyifanniubi@163.com

刘厚盾,硕士研究生,研究方向:能源与环境分析,E-mail:liuhoudun@foxmail.com

摘要

随着全球对碳排放问题的日益关注, 碳市场价格变得越来越重要. 准确可靠的碳市场价格预测不仅可以为政府宏观调控实现"双碳"目标提供更好的参考, 还可以帮助企业更有效地管理碳排放带来的风险. 本文针对碳市场价格预测, 利用经验模态分解(EMD)、卷积神经网络(CNN)和长短期记忆网络(LSTM), 提出不同的EMD-CNN-LSTM组合模型, 并探讨了CNN-LSTM组合策略, 将其分为串行策略和并行策略. 本文使用广东、上海、湖北、重庆碳交易所价格数据, 系统地对比了EMD-CNN-LSTM组合策略和单一预测模型、组合预测模型的预测效果, 验证了EMD-CNN-LSTM四种组合模型预测的精准性和稳健性, 并论证了并行策略预测对于碳市场价格序列普适性更佳.

关键词： 碳市场价格 ; 卷积神经网络 ; 长短期记忆 ; 多策略预测

Abstract

With the increasing global attention to carbon dioxide emissions, the carbon market price has become more and more important. Accurate and reliable carbon market price forecasts can not only provide a better reference for the government's macro-control to achieve the "Chinese carbon peak and carbon neutralization" goal, but also help enterprises can more effectively manage the risks brought by carbon emissions. This article uses empirical mode decomposition (EMD), convolutional neural networks (CNN) and long short-term memory networks (LSTM) to predict carbon emissions trading prices to propose different EMD-CNNs-LSTM combination strategy, and discussed the effect of the CNN-LSTM combination strategy, divide it into serial strategy and parallel strategy. This article uses the Guangdong, Shanghai, Hubei, and Chongqing carbon market price data to systematically compare the EMD-CNN-LSTM combination strategy with single prediction model and combination prediction model. The prediction effect of EMD-CNN-LSTM verifies the accuracy and robustness of the four combined strategy models of EMD-CNN-LSTM, demonstrated that parallel strategy forecasting is better for the universality of carbon market price series.

Keywords： carbon price ; convolutional neural network ; long short-term memory ; multi-strategy forecasting

PDF (3277KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈晓红, 龚思远, 贺怡帆, 曹文治, 刘厚盾. 基于CNN与LSTM多组合策略的中国碳市场价格预测. 计量经济学报[J], 2022, 2(2): 237-256 DOI:10.12012/CJoE2021-0069

CHEN Xiaohong, GONG Siyuan, HE Yifan, CAO Wenzhi, LIU Houdun. Carbon Price Forecasting in Chinese Carbon Trading Market Based on Multi-Strategy CNN-LSTM. China Journal of Econometrics[J], 2022, 2(2): 237-256 DOI:10.12012/CJoE2021-0069

1 引言

2021年两会, "碳达峰、碳中和"被重点提出, 并指出建立全国碳排放权交易市场刻不容缓. 碳市场价格预测影响国家碳排放市场交易相关的政策制定(陈晓红等(2018, 2021)), 有利于建立全国统一的碳排放权市场和减少碳排放, 帮助"双碳"目标的实现. 同时可以帮助企业分析碳排放权市场波动特征, 更有效地管理碳排放带来的风险(陈晓红等(2017), Zhang, Li and Li et al. (2020), Zhang, Li and Luo et al. (2020)). 因此, 碳市场价格预测已经成为了许多学者研究关注的问题(陈晓红等(2012), 张晨等(2016), Zhou et al. (2018), Zhu et al. (2018), Adekoya et al. (2021)).

统计和计量模型(Tang et al. (2020))在传统碳价格预测研究中就得到了利用, 如非参数统计、灰色马尔可夫等预测方法(刘金培等(2019)). 然而, 碳市场价格序列本质上具有高噪声、非线性、非平稳等特性(杨星等(2018)), 传统的统计和计量模型处理非线性模式并不具有优势. 为此, 机器学习(Zhao et al. (2019), 赵康宁等(2019))和人工智能技术(Wang et al. (2021)) 应用到了碳市场价格预测中(朱帮助等(2011), Zhu et al. (2017)), 现有的碳市场价格预测方法分为单一预测模型和组合预测模型. 其中常用的单一预测模型包括长短期记忆(long short-term memory, LSTM)神经网络(Huang et al. (2021), Shahid et al. (2021))、BP (back propagation)神经网络等预测模型.

采用单一预测模型进行价格预测时, 会把原始碳价时间序列中不同特征的信息同质化, 进而影响预测结果的精准性. 因此, 近年来一些学者将组合预测模型(Anand et al. (2017), Sun et al. (2018))引入到碳市场价格预测(Zhang et al. (2018), Hao et al. (2020))研究领域, 典型的有相空间重构(phase space reconstruction, PSR)和最小二乘支持向量回归(least square support vector regression, LSSVR)组合模型(石雪涛等(2017)), 多贝西小波三层变换和单支重构的遗传算法径向基函数神经网络(Daubechies wavelet genetic algorithm radial basis function neural network model, Db3-GA-RBF)组合模型(杨星等(2018)), 多分辨率奇异值分解(multi-resolution singular value decomposition, MRSVD)和极限学习机(extreme learning machine, ELM)组合模型(Zhang et al. (2019)), 碳价格网络极限学习机(carbon price network-extreme learning machine, CPN-ELM)模型、快速多输出关联向量回归(fast multi-output relevance vector regression, FMRVR)和多目标鲸鱼优化算法(multi-objective whale optimization algorithm, MOWOA) 组合模型(Xiong et al. (2019)).

对于神经网络和上述组合模型, 碳市场价格数据不稳定产生的滞后效应会很大程度影响预测效果的精准性. 为此当前研究采用小波分解和经验模态分解(empirical mode decomposition, EMD)等方法, 对时间序列进行多尺度分解, 分解后的序列拥有更优秀的尺度波动规律性. 相比于小波分解方法, EMD对于分解尺度不需要预先设定, 在适应性、拟合精度等方面具有一定优势(李合龙等(2019)). 当前EMD-GA (genetic algorithm, 遗传算法) - BP、EMD-CNN (convolutional neural network, 卷积神经网络) - LSTM (刘亚珲等(2021))等组合模型广泛应用于不同领域的数据预测. 其中EMD-GA-BP与EMD-PSO (particle swarm optimization, 粒子群算法) - LSSVM组合模型(崔焕影和窦祥胜(2018))、EMD-PSO-SVM组合模型(Yang et al. (2014)) 在碳市场价格预测中取得了良好的预测效果.

基于上述文献综述, 本文认为孙少龙等(2021)提出的分解-预测-集成思想的多组合机器学习预测模型在提高中国区域性碳市场价格预测精度上具有显著优势. 然而, 现有研究仍存在一定的局限性:

1) CNN-LSTM组合模型在众多领域的预测性能获得了验证, 但是对于中国碳市场价格预测领域的效果研究还存在空缺.

2) CNN和LSTM具有很强的数据特征提取能力, 其中CNN能提取数据空间特性, LSTM提取时间特性. 现有研究对于CNN-LSTM组合方式进行了不同探索, 但未系统分析CNN-LSTM不同组合结构的特点和预测性能, 未能形成较完整的CNN-LSTM组合策略.

鉴于已有研究的不足, 本文构建了EMD-CNN-LSTM组合模型, 主要贡献可以归纳为以下三个方面:

1) 为了比较CNN和LSTM组合网络结构的特性, 本文在相关研究的基础上, 归纳并提出了CNN-LSTM串行和并行策略, 从串行策略和并行策略角度对比分析了CNN-LSTM模型对于碳市场价格预测的适用性.

2) 在CNN-LSTM串行和并行策略的基础上, 结合EMD分解技术, 组合出多种EMD-CNN-LSTM预测模型. 这些容易复制的模型结构可以扩展到大多数类型的CNN-RNN网络, 用于具有多个输入特征的预测任务, 为碳市场价格预测提供了有用的参考.

3) 采用了国内广东、上海、重庆、湖北四大碳交易所数据, 验证了本文所提EMD-CNN-LSTM模型的精确性和稳定性.

后续章节内容分别为: 第2部分首先介绍了EMD-CNN-LSTM模型的构成方法, 归纳了CNN-LSTM组合策略, 然后详细介绍了四种不同的EMD-CNN-LSTM模型. 第3部分以四所碳交易所的碳市场价格作为样本数据, 开展实证分析, 系统化检验不同CNN-LSTM策略结构的预测性能, 并将EMD-CNN-LSTM与其他基准模型进行对比, 验证该模型预测性能的准确性和稳定性. 最后是本文的总结.

2 模型构建

2.1 经验模态分解(EMD)

碳交易额受到多方面因素的影响, 例如碳排放量、能源计价、经济发展等, 表现出非线性、波动性的特点, 非线性和波动性会影响碳交易额预测的准确性, 因此需要利用EMD (张雯等(2021))对碳市场价格数据进行多尺度分解, 将碳市场价格序列数据分解为不同频率的振动模块和残差项, 用于后续的碳市场价格预测. EMD的核心思想是将不稳定的数据序列分离出不同尺度的平稳波动项以及一个残差趋势项, 波动项即本征模态函数(intrinsic mode function, IMF).

EMD的具体分解过程如下:

步骤1  确定初始待分解序列$ H(t) $及序列上所有局部极值点, 使用三次样条插值连接所有局部极值点形成上下包络线$ m_{\rm u p}(t) $, $ m_{\rm l o w}(t) $.

步骤2  求出包络线的均值曲线

$ \begin{equation} m(t) = \left(m_{\rm u p}(t)+m_{\rm l o w}(t)\right) / 2. \end{equation} $

步骤3  求出初始序列与包络均值曲线的差值

$ \begin{equation} h_{k}(t) = H(t)-m(t). \end{equation} $

若其不满足IMF分量的两个条件, 即极值和过零点的数目必须相等或者最多相差1, 其次包络平均值必须为0. 则用$ h_k (t) $代替$ H(t) $, 重复步骤1与2, 直至$ k $次迭代后$ h_k (t) $满足两个条件.

步骤4  IMF1分量为

$ \begin{equation} C_{1} = h_{k}(t). \end{equation} $

相对应剩余分量为

$ \begin{equation} r_{1}(t) = H(t)-C_{1}. \end{equation} $

步骤5  重复步骤1 $ \sim $步骤4将剩余分量$ r_{1}(t) $作为原始序列进行分解, 获得$ n $个IMF分量和一个残差分量$ r_{n}(t) $, 其中残差分量为单调序列或者常值序列.

步骤6  最终得到EMD分解公式如下:

$ \begin{equation} H(t) = \sum\limits_{i = 1}^{N} C_{i}+r_{n}(t). \end{equation} $

经过上述步骤, 本文利用EMD将碳市场价格初始序列$ H(t) $分解为若干个$ C_i $分量和代表碳市场价格整体变化趋势的$ r_n (t) $. 然后借助CNN和LSTM神经网络对若干分量进行特征提取和预测.

2.2 卷积神经网络(CNN)

CNN (convolutional neural networks)是一种能自动进行特征提取的技术, 在图像视觉领域取得了巨大的成功, 它在处理时间序列方面也显示出强大的潜力.本文通过卷积运算从相邻时间点的碳市场价格中提取空间特征, 输出特征图, 提取EMD相邻IMF中存在的显著空间关系特征. 一维卷积和二维卷积公式如下:

$ \begin{eqnarray} &&y_{i}^{(n+1)}(\tau) = \delta\left(x_{i}^{n}+\sum\limits_{f = 1}^{F^{n}} K_{f = 1}^{n}(\tau) * y_{f}^{n}(\tau)\right) \end{eqnarray} $

$ \begin{eqnarray} && \; \; \; \; \; \; \; \; \; \; \; \; \; = \delta\left(x_{i}^{n} \sum\limits_{f = 1}^{F^{n}}\left[\sum\limits_{l = 1}^{l^{n}} K_{j i}^{n}(l) y_{f}^{n}(\tau-l)\right]\right), \end{eqnarray} $

$ \begin{eqnarray} &&y_{i}^{(n+1)}(a, b) = \delta\left(x_{i}^{n}+\sum\limits_{f = 1}^{F^{n}} K_{f = 1}^{n}(a, b) * y_{f}^{n}(a, b)\right) \end{eqnarray} $

$ \begin{eqnarray} &&\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; = \delta\left(x_{i}^{n} \sum\limits_{f = 1}^{F^{n}}\left[\sum\limits_{l = 1}^{l^{n}} \sum\limits_{w = 1}^{w^{n}} K_{j i}^{n}(l, w) y_{f}^{n}(a-l, b-w)\right]\right), \end{eqnarray} $

其中, $ y_i^{(n+1)}(\tau) $表示$ n+1 $层中的特征图$ i $, $ \delta $表示非线性激活函数, $ F^n $表示$ n $层当中的特征图的数量, $ K_{j i}^{n} $表示在$ n $层中的特征图$ f $以创建$ n+1 $中的特征图$ i $, $ x_i^n $表示偏差向量, $ l $表示一维卷积层中核的长度, $ w $表示二维卷积中核的宽度.

2.3 长短期神经网络(LSTM)

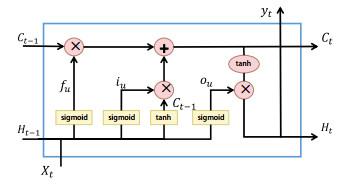
LSTM (long-short term memory)是一种改进的循环神经网络(recurrent neural network, RNN). 单元结构如图 1所示:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   LSTM网络结构图


LSTM网络结构的主要特点是在RNN原有的结构中加入的三个"门"结构, 分别是遗忘门、输入门和输出门.

遗忘门决定了上一层结构的输出中有哪些信息可以进入当前结构, 控制内部状态信息; 输入门是决定有多少新的信息加入到该层中来, 控制输入信息; 输出门用来决定本层的信息有多少输出到下一层去, 控制输出信息. LSTM模型因为其三个门结构的设计, 提升了传统RNN神经网络对长时间序列的学习能力. 这三个门的功能在数学上表述如下:

$ \begin{eqnarray} &&f_{u} = \operatorname{sigmoid}\left(W_{f}\left[x_{t}+H_{t-1}\right]+b_{f}\right), \end{eqnarray} $

$ \begin{eqnarray} && i_{u} = \operatorname{sigmoid}\left(W_{i}\left[x_{t}+H_{t-1}\right]+b_{i}\right), \end{eqnarray} $

$ \begin{eqnarray} &&o_{u} = \operatorname{sigmoid}\left(W_{o}\left[x_{t}+H_{t-1}\right]+b_{o}\right), \end{eqnarray} $

$ \begin{eqnarray} &&c_{t} = c_{t-1} \otimes f_{u}+i_{u} \otimes\left(\tanh \left(W_{c}\left[x_{t}+H_{t-1}\right]+b_{c}\right)\right), \end{eqnarray} $

$ \begin{eqnarray} &&H_{t} = o_{t} \otimes \tanh \left(c_{t-1}\right). \end{eqnarray} $

在式(10)到(13)中, 三个单元和存储单元的权重矩阵和偏置变量分别为$ \{W_{f}, W_{i}, W_{o}, W_{c}\} $和$ \{b_{f}, b_{i}, b_{o}, b_{c}\} $. $ H_{t-1} $为之前的隐藏单元, 按元素顺序添加三个单元的权重, $ c_t $为处理后的当前单元. 隐层的输入单元、单元格单元和输出单元之间的元素级乘法用$ \otimes $表示. 核函数用正切函数tanh和sigmoid型函数表示. 方程(10)到(12)分别表示遗忘、输入和输出单元. 式(13) (14) 表示$ t $时间步长时的当前存储单元和隐藏单元.

2.4 CNN-LSTM组合策略

CNN和LSTM具有强大的提取数据特征的能力, 尤其是, CNN可以直接学习时间序列数据的内部表示, 不需要领域的专业知识来手动提取特征, 而LSTM有较强的时间特征提取能力, 可以更准确地捕捉时间序列趋势中隐含的信息. 将CNN和LSTM结合使用能充分利用这两个神经网络的优势, 充分挖掘数据的潜在特质, 为预测提供支撑.

本文在相关研究的基础上分析了CNN-LSTM模型的各种策略, 将CNN-LSTM组合策略分为串行和并行两种策略.

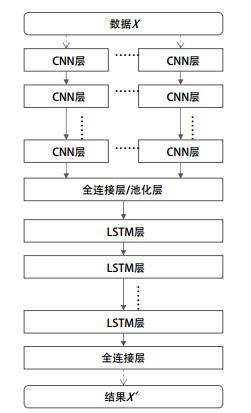
串行策略指数据顺序经过CNN网络结构和LSTM网络结构, 如图 2, CNN网络结构可由一个或多个CNN网络组成, 为了提取不同特征, 一般CNN网络采用不同的卷积核, 在CNN网络提取特征后, 通过池化层或者全连接层将多个CNN网络融合; 然后, 融合结果通过LSTM进行学习; 最后通过全连接层得到最终结果.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   CNN-LSTM串行组合策略结构


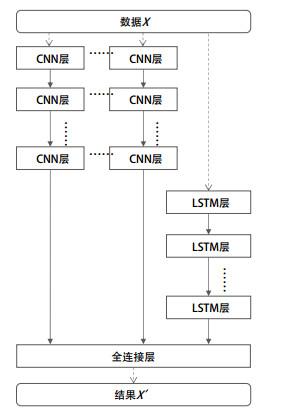
并行策略(如图 3)是数据同时由CNN网络结构和LSTM网络结构处理. 与串行策略一样, CNN可采用多个CNN网络组成, 通过池化层将多个CNN网络融合. 在经过CNN和LSTM网络学习后, 通过全连接层将数据合并得到最终结果.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   CNN-LSTM并行组合策略结构


2.5 EMD-CNN-LSTM组合预测模型

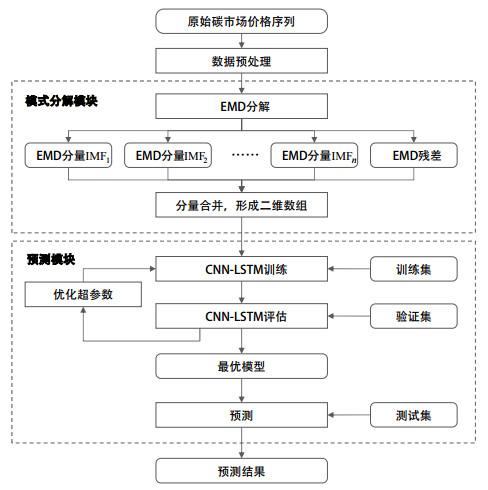
为了保证CNN-LSTM模型的函数拟合和后续收敛, 本文使用EMD将数据分解成简单的频率特征, 并结合上节讨论的CNN-LSTM组合策略形成EMD-CNN-LSTM组合预测模型. 本文所构建的EMD-CNN-LSTM组合预测模型包含两个模块: 1)模式分解模块: 考虑碳市场价格的非线性和非平稳特性, 本文采用EMD技术对原始序列进行分解处理, 形成不同频率的子序列和残差. 2)预测模块: 应用CNN-LSTM串行或并行组合策略对各个子序列和残差项进行预测. EMD-CNN-LSTM组合预测模型的基本结构如图 4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   EMD-CNN-LSTM模型结构图


EMD-CNN-LSTM模型包括以下四个主要步骤:

步骤1  EMD分解. 碳交易额序列经过预处理后, 被EMD分解成两组组成部分: 一系列的分量IMF和一个残差.

步骤2  分量合并. 合并EMD分解获得的分量IMF和残差, 形成二维数组, 并划分为训练数据集、测试数据集.

步骤3  模型训练. 将训练数据集输入CNN-LSTM网络进行训练学习, 并通过验证数据集对CNN-LSTM拟合进行无偏估计, 以此调整模型超参数. 通过训练和评估得到CNN-LSTM神经网络的最优超参数, 形成预测模型.

步骤4  输入待预测数据, 使用预测模型进行预测, 最后得到预测结果.

根据不同的CNN-LSTM网络结构, 本节提出四种EMD-CNN-LSTM神经网络结构模型, 具体结构如下.

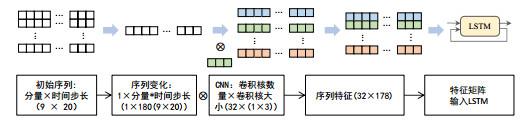
首先, 利用CNN-LSTM串行结构构建简单的预测模型EMD-CNN-LSTM-Ⅰ, 本文将EMD子序列进行变化, 将子序列合并为1维序列, 并输入到CNN-LSTM串行结构中进行预测, 该模型的特点是不改变CNN-LSTM串行结构, 可以使用传统的预测结构. 具体结构如图 5.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   CNN-LSTM-Ⅰ结构图(图中参数皆为举例)


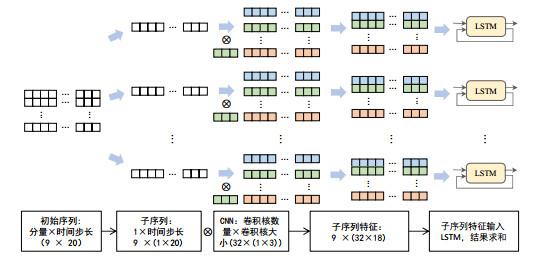
参照Xie et al. (2020)等人提出的CNN-LSTM预测模型, 本文提出当前最常用的EMD-CNN-LSTM网络结构(EMD-CNN-LSTM-Ⅱ), 该模型的特点是以CNN-LSTM串行结构为处理单元, 对每个EMD子序列进行预测. 首先将原始碳价格序列分解成具有不同频率的子序列, 然后将每个子序列输入CNN-LSTM串行结构的处理单元当中, 使用一维卷积提取相邻数据的关联特征, 再通过LSTM对特征时间序列进行处理, 得到分量的预测结果, 最后对子序列的预测结果进行重构. 具体结构如图 6.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   CNN-LSTM-Ⅱ结构图(图中参数皆为举例)


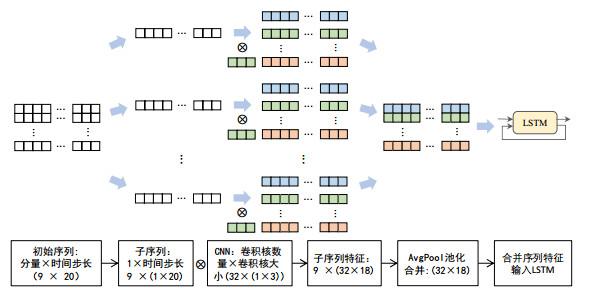
由于在EMD-CNN-LSTM-Ⅱ中, 割裂了各个EMD分量之间的关系, 本文提出第三个网络结构EMD-CNN-LSTM-Ⅲ中, 意在将EMD分量在LSTM阶段对EMD分量组合分析. 本文将EMD子序列通过CNN结构, 使用一维卷积提取其特征, 而后合并为二维数组, 并输入LSTM进行预测, 最后通过全连接层进行预测值合成. 具体结构如图 7.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   CNN-LSTM-Ⅲ结构图(图中参数皆为举例)


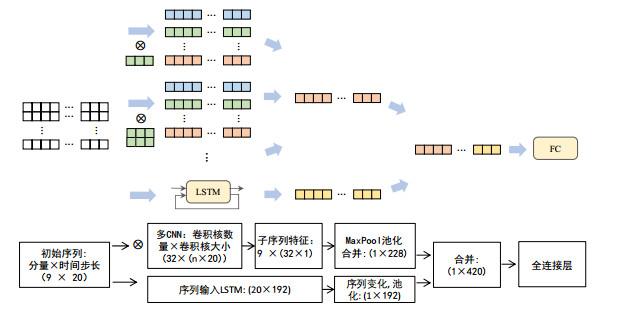
以上3个预测模型均基于CNN-LSTM串行结构进行构建, 本文提出的第四个网络结构EMD-CNN-LSTM-Ⅳ采用CNN-LSTM并行策略进行构建. 以EMD分量组合的二维矩阵为CNN和LSTM部分的输入, 分别提取EMD分量的时空特征, 在提取完成后将两部分特征融合, 并通过全连接层进行预测值合成. 具体结构如图 8.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   CNN-LSTM-Ⅳ结构图(图中参数皆为举例)


3 实证分析

3.1 数据来源

本文采集汇总了国内广东、重庆、上海、湖北四所碳交易所的碳市场价格数据, 交易数据时间跨度从2017年3月至2021年3月. 四所碳交易所价格数据来源于国内各碳交易所官网权威平台数据. 数据特征丰富, 包含交易时间、成交价等对价格影响因素. 其中, 广东碳交易所数据集1030条数据, 重庆碳交易所数据集1022条数据, 上海碳交易所数据集1023条数据, 湖北碳交易所数据集1025条数据, 为了测试组合模型的预测质量, 选择四个数据集中前700条集合数据用于训练, 后300条数据集合用于测试.

3.2 评价指标

为了证明EMD-CNN-LSTM模型的有效性, 本文选择了CNN、LSTM、GRU、CNN-LSTM、CNN-GRU等五个不同的模型为基准模型. 其中, CNN、LSTM、GRU为单一预测模型, CNN-LSTM、CNN-GRU为组合预测模型.本文使用均方根误差(RMSE)、平均绝对误差(MAE)和均方误差(MSE)用于评估预测误差, 值越小, 代表模型预测结果越准确.

$ \begin{eqnarray} &&{\rm M A E} = \frac{1}{n} \sum\limits_{i = 1}^{n}\left|\widehat{y}_{i}-y_{i}\right|, \end{eqnarray} $

$ \begin{eqnarray} && {\rm R M S E} = \sqrt{\frac{1}{n} \sum\limits_{i = 1}^{n}\left(\widehat{y}_{i}-y_{i}\right)^{2}}, \end{eqnarray} $

$ \begin{eqnarray} && {\rm M S E} = \frac{1}{n} \sum\limits_{i = 1}^{n}\left(\widehat{y_{i}}-y_{i}\right)^{2}, \end{eqnarray} $

其中$ \hat{y_i } $和$ y_i $表示碳市场价格的真实值和预测值, $ n $是本文测试样本的数据量大小, $ i $为测试样本点序列号.

3.3 模型参数

本文采用PyTorch1.8实现预测模型. 为了防止优化函数陷入局部最优值, 提高预测的准确性, 本文采用批梯度下降法训练神经网络的权值和偏置, 批大小数为30, 学习率为0.0001, 遗弃率为0.6, 选用Adam优化器作为优化器, 共训练300到500期. 对于不同的CNN和RNN网络结构参数如表 1.

表1   不同模型下的CNN和RNN网络结构参数

模型CNN层RNN层
LSTM-单LSTM结构:
隐藏层2层, 单元个数192
GRU-单GRU结构:
隐藏层2层, 单元个数192
CNN单CNN结构:
出口通道32, 卷积核为(1, 3)		-
CNN-LSTM单CNN结构:
输出通道32, 卷积核为(1, 3)		单LSTM结构:
隐藏层2层, 单元个数192
CNN-GRU单CNN结构:
输出通道32, 卷积核为(1, 3)		单GRU结构:
隐藏层2层, 单元个数192
EMD-CNN-LSTM-Ⅰ单CNN结构:
输出通道32, 卷积核为(1, 3)		单LSTM结构:
隐藏层2层, 单元个数192
EMD-CNN-LSTM-Ⅱ每个分量单CNN结构:
输出通道32, 卷积核为(1, 3)		每个分量单LSTM结构:
隐藏层2层, 单元个数192
EMD-CNN-LSTM-Ⅲ每个分量单CNN结构:
输出通道32, 卷积核为(1, 3)		单LSTM结构:
隐藏层2层, 单元个数192
EMD-CNN-LSTM-Ⅳ多CNN结构: 输出通道32,
卷积核依次为(1, 20)、(2, 20) $ \cdots$		单LSTM结构: 隐藏层2层,
单元个数192

新窗口打开| 下载CSV


由于不同城市碳市场价格数据特点不同, 对于预测模型参数会进行微调. 其次全连接层一般采用两层Liner进行处理, CNN后和Liner层后会使用激活函数ReLu.

3.4 EMD分量分解

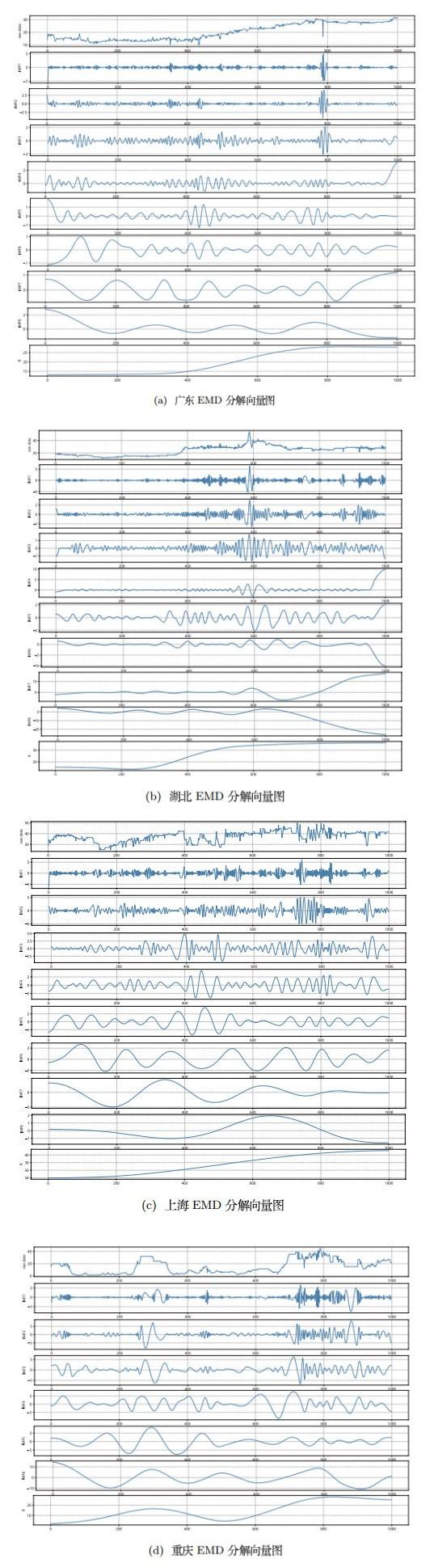
本文采用EMD分解技术分别对广东、湖北、上海、重庆四个碳市场价格序列进行了向量分解, 第一行Raw data表示碳市场价格原始数据趋势, 中间行表示IMF, 最后一行表示残差. 其中, 广东、湖北、上海有8个IMF和1个残差, 重庆有6个IMF和1个残差.

如图 9所示, 广东碳市场因其配额分配方案呈"稳中偏紧"的特性, 碳市场交易一直呈现稳定行情. 湖北碳市场自开市以来就采取"低价起步、适度从紧"的分配策略, 是四所碳市场中交易集中度最低的, 活跃度相对较高. 详细的监管制度和严格处罚力度使得上海碳市场表现一直活跃. 重庆碳市场受其配额分配机制"先松后紧", 交易体系目标不以交易为主的影响, 自开市以来碳市场处于极度不活跃状态. 从EMD分解结果上分析可知, 越后分解出的IMF分量振荡幅度越平缓. 与原始数据特征相似, 不同碳市场的IMF分量呈现出各自市场的特征, 广东分量整体保持稳定, 波动区间具有集中性; 湖北分量表现出强烈的活跃上升特性, 呈现整体平稳但波动性逐渐增强的趋势; 上海分量具有较强的离散性, 并且后期周期性愈发明显; 重庆分量表现平缓, 变化趋势都集中在后面阶段, 且规律性较混乱.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   所有城市碳市场价格EMD分解向量结果图


3.5 实证检验

本文对所有模型进行了向前1步的预测检验, 即将前20个交易日(四周)的数据用于预测第21个交易日的碳市场价格. 各个模型对广东、重庆、上海、湖北的碳市场价格预测结果对比如图 10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   不同模型对碳市场价格预测结果对比


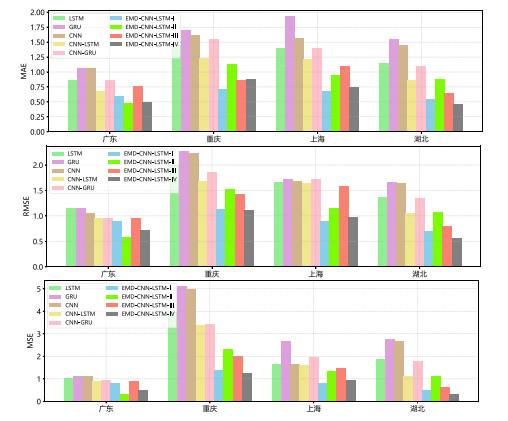
另外, 表 2显示了各个预测模型对碳市场价格预测的MAE、MSE、RMSE评价值. 在单一预测模型中, CNN和LSTM在四个城市碳市场价格预测性能表现较好, 说明CNN和LSTM对碳市场价格数据有较好的特征提取能力. 在组合预测模型中CNN-LSTM组合模型效果较好, 同时好于单一预测模型, 说明CNN-LSTM组合预测模型能同时对碳市场价格数据进行时空特征提取. 对于湖北数据, 分量图和数据分布图显示, 湖北稳定活跃的时期占据了大多数时间, 但是与其他城市不一样的是部分分量呈现单向的骤降和骤升, 使得EMD-CNN-LSTM-Ⅱ组合模型对分量采用CNN-LSTM结构进行预测时误差会增加, 同时预测结果累加会使误差叠加, 使EMD-CNN-LSTM-Ⅱ方法的结果略差于CNN-LSTM方法.

表2   不同模型碳市场价格预测结果评价指标对比表

模型广东重庆
MSERMSEMAEMSERMSEMAE
LSTM1.02491.15100.85343.96161.99041.4534
GRU1.10601.15181.06595.10852.26021.6947
CNN1.10321.05031.05874.96732.22871.6122
CNN-LSTM0.90120.94930.67913.38591.67121.2351
CNN-GRU0.95640.96080.86883.43821.85431.5388
EMD-CNN-LSTM-Ⅰ0.79250.89020.58881.38671.12450.7186
EMD-CNN-LSTM-Ⅱ0.3323*0.5765*0.4821*2.32361.52431.1283
EMD-CNN-LSTM-Ⅲ0.89480.94590.76032.01971.42110.8637
EMD-CNN-LSTM-Ⅳ0.50350.70950.49231.2378*1.1126*0.8783*
模型上海湖北
MSERMSEMAEMSERMSEMAE
LSTM1.65911.66581.39881.85711.36271.1480
GRU2.68151.72771.92432.76761.66361.5537
CNN1.66531.67311.55872.68111.63741.4551
CNN-LSTM1.61691.63301.21931.10901.05300.8692
CNN-GRU1.96471.72181.39761.80761.34451.0981
EMD-CNN-LSTM-Ⅰ0.8050*0.8972*0.6713*0.48710.69790.5503
EMD-CNN-LSTM-Ⅱ1.33681.15620.94081.13461.06890.8706
EMD-CNN-LSTM-Ⅲ1.47341.57271.10320.62670.79160.6379
EMD-CNN-LSTM-Ⅳ0.96190.98070.74760.3128*0.5593*0.4581*

新窗口打开| 下载CSV


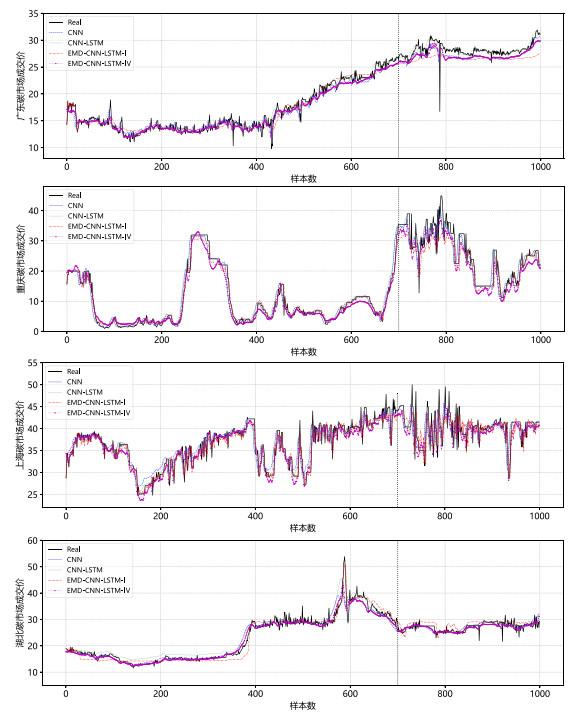
整体实证结果表明, 在对碳市场价格的预测, 本文提出的四个EMD-CNN-LSTM组合模型在所有城市都取得了优于其他基准模型的预测结果, 说明EMD-CNN-LSTM组合模型预测性能更优.根据以上结果分析, 本文选取CNN、CNN-LSTM、EMD-CNN-LSTM-Ⅰ、EMD-CNN-LSTM-Ⅳ模型绘制了广东、重庆、上海、湖北碳市场价格预测结果图.

如图 11所示, 在各个碳交易市场价格预测中, EMD-CNN-LSTM-Ⅳ组合模型的预测曲线与真实值曲线吻合度较高, 即EMD-CNN-LSTM-Ⅳ组合模型预测精度较好, 与前述分析结果一致.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同模型碳市场价格预测结果


3.5.1 未经分解与分解组合模型的对比

CNN-LSTM组合模型和CNN-GRU组合模型均是直接利用碳市场价格序列作为预测模型输入的预测模型, 通过比较表 2的预测结果可知CNN-LSTM组合模型和CNN-GRU组合模型预测精度优于单一的预测模型, 在重庆和湖北交易所碳市场价格预测中性能提升尤为显著. 结构上, CNN-LSTM与EMD-CNN-LSTM模型Ⅰ、Ⅱ、Ⅲ均属于串行策略, 而采用了EMD分解技术的EMD-CNN-LSTM组合模型提高了整体模型的预测精度, 预测效果好于未经分解技术的CNN-LSTM组合模型和CNN-GRU组合模型, 这说明分解技术能有效降低碳市场价格序列的复杂度, 提高预测精度.

3.5.2 CNN-LSTM串行策略与并行策略对比分析

EMD-CNN-LSTM组合模型分为串行策略和并行策略两大类. 其中, 并行策略以EMD-CNN-LSTM-Ⅳ组合模型为代表, 其他三种均为串行策略.

对比表 2可知, EMD-CNN-LSTM模型相较于单一神经网络预测模型, 多尺度的组合模型EMD-CNN-LSTM无论在预测的拟合程度还是减小误差方面均有较大的优势. 结合表 2和图 10可得, EMD-CNN-LSTM-Ⅰ组合模型在离散性较强的上海碳市场价格预测结果中相比其他串行策略取得了最优结果, 同时预测效果也强于并行策略EMD-CNN-LSTM-Ⅳ组合模型; 串行策略EMD-CNN-LSTM-Ⅱ组合模型的在起伏趋势平稳的广东碳市场价格预测结果中MSE、MAE、RMSE评价值与基准模型相比只占了30%, 在所有模型中为最小, 而并行策略EMD-CNN-LSTM-Ⅳ组合模型的预测结果仅次于EMD-CNN-LSTM-Ⅱ组合模型. 除此之外, 并行策略EMD-CNN-LSTM-Ⅳ组合模型在价格变化不活跃的重庆碳市场和活跃的湖北碳市场价格预测中对比其他所有串行策略均取得了最好结果; 串行策略EMD-CNN-LSTM-Ⅲ组合模型碳市场价格预测结果虽然优于单一模型和未经分解模型, 但是在四种策略结果中表现一般.

串行策略中, EMD-CNN-LSTM-Ⅰ组合模型的预测过程采用将所有分量组合成一维特征作为预测输入, 传进CNN-LSTM模型中进行训练, 因其结构的简洁性, 在计算上能很好地适应离散型较强的数据. EMD-CNN-LSTM-Ⅱ组合模型采用将EMD算法分解后的多维向量作为输入, 随后CNN和LSTM在单个分解组件中对碳市场交易价格序列进行训练, 最后由多个LSTM模块累加得到预测结果, 此种累加结构的优势是能对具有分布均匀特性的数据进行更好的预测, 但累加结构会造成结果误差的叠加. EMD-CNN-LSTM-Ⅲ组合模型是对碳市场价格序列应用EMD分解算法后, 将所得子序列合并输入CNN-LSTM结构中, 这种合并结构让LSTM结构部分处理结果比较简洁, 从而会忽略个别数据特性, 在表现上略差一筹. 与它们不同的是, 并行策略结构的EMD-CNN-LSTM-Ⅳ组合模型采用将经过分解后的向量并行输入CNN和LSTM模型中, 最后将两者结果进行累加得到预测结果, 并行结构的使用, 使得此策略结构能照顾到更多的数据特性细节, 从而具备了更好的适应性, 因此在大多数数据集上都表现优秀.

3.5.3 模型时间复杂度对比分析

由于EMD-CNN-LSTM组合模型采用了组合策略, 增加了预测模型的复杂度. 为此, 本节通过实验对比了EMD-CNN-LSTM组合模型训练运行时间和时间复杂度. 本文对LSTM等单一模型和EMD-CNN-LSTM组合模型分别进行了500、750、1000条数据三个量级的时间复杂度实验, 结果如表 3所示.

表3   不同模型碳市场价格时间复杂度对比表

模型广东(秒)重庆(秒)
50075010005007501000
LSTM233651223651
GRU203447213346
CNN254058244156
CNN-LSTM274562274560
CNN-GRU244156254055
EMD-CNN-LSTM-Ⅰ71.2108.54150.1957.46101.27130.71
EMD-CNN-LSTM-Ⅱ282.15476.54758.75237.61365.46584.76
EMD-CNN-LSTM-Ⅲ95.12147.1198.796.16140.63199.33
EMD-CNN-LSTM-Ⅳ141.54213.64304.49143.86211.59296.95
模型上海(秒)湖北(秒)
50075010005007501000
LSTM233651223752
GRU203345203446
CNN263958254159
CNN-LSTM294462284461
CNN-GRU253955264055
EMD-CNN-LSTM-Ⅰ66.17107.7135.5769.55104.11137.68
EMD-CNN-LSTM-Ⅱ242425.32758.84257.37489.97734.28
EMD-CNN-LSTM-Ⅲ87.24143.44198.3696.14143.66195
EMD-CNN-LSTM-Ⅳ135.88217.01295.32142.53215.43293.03

新窗口打开| 下载CSV


对比四个碳市场交易价格预测模型的训练运行时间可知不同城市数据特性和数据分布对于模型训练运行时间影响不大, 对比三个数据量级模型运行时间可知, 未经分解的预测模型运行时间随着数据量级提升呈现线性增长, 本文提出的EMD-CNN-LSTM-Ⅰ、Ⅲ、Ⅳ组合模型也呈现此特点, 而EMD-CNN-LSTM-Ⅱ组合模型运行时间会随着数据量级增加而成倍数增加. EMD-CNN-LSTM-Ⅰ、Ⅲ、Ⅳ组合模型采用了经过EMD分解后的多个向量作为输入, 相比其他基准模型在输入量上成倍增加, 另外模型结构也相较于单一模型复杂, 所以这些模型的训练运行时间比单一模型长. 但是对比分析所有模型的同量级运行时间可知, 本文提出的EMD-CNN-LSTM组合模型相比于单一模型和未经分解模型, 在多出EMD分解向量运行负荷的步骤下, 运行时间并没有呈现成倍增加, 而是正常范围内的结构性组合导致的运行时间叠加增长, 显现了本文策略结构在提升预测精度和稳定性的同时具有较好的时间复杂度.

其中, EMD-CNN-LSTM-Ⅱ组合模型对多个分量采用CNN-LSTM进行预测, 并对分量预测结果进行求和, 所以EMD-CNN-LSTM-Ⅱ组合模型对于高量级数据的运行和分析需要更长的时间.

4 结论

本文主要提出了一种基于EMD-CNN-LSTM的碳市场价格序列预测模型. 该模型采用EMD分解技术, 并结合CNN-LSTM模型进行预测. 以广州、上海、重庆、湖北碳交易所的碳市场价格作为实证样本, 从串行策略和并行策略角度出发, 将两类EMD-CNN-LSTM模型与CNN-LSTM、CNN-GRU、GRU、CNN、LSTM模型的预测性能进行了比较. 本文主要贡献如下:

1) 证明与GRU、CNN、LSTM等单一预测模型和CNN-LSTM、CNN-GRU等组合模型相比, EMD-CNN-LSTM组合模型预测误差较小, 预测结果更准确.

2) EMD-CNN-LSTM-Ⅳ组合模型对于活跃度较高的湖北碳市场价格预测和活跃度不好的重庆碳市场价格预测中均获得良好的预测效果, 说明并行策略对于不同特性的碳市场价格序列具有良好的普适性.

3) 相比其他串行策略, 串行策略EMD-CNN-LSTM-Ⅰ组合模型针对离散特性的碳市场价格序列具有更好的预测表现, 串行策略EMD-CNN-LSTM-Ⅱ组合模型对于表现平稳的碳市场价格序列预测效果更好.

此外, 本文的研究结果为提高碳市场价格预测的准确性提供了一种新的途径, 丰富了CNN和LSTM组合网络结构特性的比较研究, 这种容易扩展的策略可以应用于更多领域的CNN-LSTM预测模型中. 然而, 由于本文暂时未将碳市场价格变化季度特性, 国内不同碳市场覆盖行业特性等纳入比较指标, 因此, 在未来研究方向上, 可以在串行策略和并行策略CNN-LSTM组合模型基础上, 从不同行业特性下碳市场价格序列预测适用性的角度出发, 进一步提升预测效果.

参考文献

崔焕影, 窦祥胜,

基于EMD-GA-BP与EMD-PSO-LSSVM的中国碳市场价格预测

[J]. 运筹与管理, 2018, 27 (7): 133- 143.

URL     [本文引用: 1]

Cui H Y , Dou X S ,

Carbon Price Forecasts in Chinese Carbon Trading Market Based on EMD-GA-BP and EMD-PSO-LSSVM

[J]. Operations Research and Management Science, 2018, 27 (7): 133- 143.

URL     [本文引用: 1]

陈晓红, 汪静, 胡东滨,

碳配额免费分配法下寻租对市场运行效率影响

[J]. 系统工程理论与实践, 2018, 38 (1): 93- 101.

URL     [本文引用: 1]

Chen X H , Wang J , Hu D B ,

Study on the Effect of Rent-Seeking on Carbon Emission Trading Market Performance Under Free Carbon Emission Allowances

[J]. Systems Engineering — Theory & Practice, 2018, 38 (1): 93- 101.

URL     [本文引用: 1]

陈晓红, 王钰, 李喜华,

环境规制下区域间企业绿色技术转型策略演化稳定性研究

[J]. 系统工程理论与实践, 2021, 41 (7): 1732- 1749.

URL     [本文引用: 1]

Chen X H , Wang Y , Li X H ,

Research on Green Technology Transformation Strategy of Inter-Regional Enterprises Under Enviromental Regulation Based on Evolutionary Gamen Theory

[J]. Systems Engineering — Theory & Practice, 2021, 41 (7): 1732- 1749.

URL     [本文引用: 1]

陈晓红, 王陟昀,

碳排放权交易价格影响因素实证研究——以欧盟排放交易体系(EUETS)为例

[J]. 系统工程, 2012, 30 (2): 53- 60.

URL     [本文引用: 1]

Chen X H , Wang Z Y ,

Empirical Research on Price Impact Factor of Carbon Emission Exchange: Evidence from EUETS

[J]. Systems Engineering, 2012, 30 (2): 53- 60.

URL     [本文引用: 1]

陈晓红, 易国栋, 刘翔,

基于三阶段SBM-DEA模型的中国区域碳排放效率研究

[J]. 运筹与管理, 2017, 26 (3): 115- 122.

URL     [本文引用: 1]

Chen X H , Yi G D , Liu X ,

Analysis of the Low Carbon Economy Efficiency in China: Based on a Method of Three Stage SBM-DEA Model with Undesirable Outputs

[J]. Operations Research and Management Science, 2017, 26 (3): 115- 122.

URL     [本文引用: 1]

刘金培, 郭艺, 陈华友, 任贺松, 陶志富,

基于非结构数据流行学习的碳价格多尺度组合预测

[J]. 控制与决策, 2019, 34 (2): 279- 286.

URL     [本文引用: 1]

Liu J P , Guo Y , Chen H Y , Ren H S , Tao Z F ,

Multi-Scale Combined Forecast of Carbon Price Based on Manifold Learning of Unstructured Data

[J]. Control and Decision, 2019, 34 (2): 279- 286.

URL     [本文引用: 1]

李合龙, 杨能, 林楚汉, 张卫国,

我国股票市场行业间波动溢出效应研究——基于改进的EMD去噪方法

[J]. 系统工程理论与实践, 2019, 39 (9): 2179- 2188.

URL     [本文引用: 1]

Li H L , Yang N , Lin C H , Zhang W G ,

A Survey on Industrial Spoillover Effect of China's Stock Market — Based on Revised EMD Denoising Methon

[J]. Systems Engineering — Theory & Practice, 2019, 39 (9): 2179- 2188.

URL     [本文引用: 1]

刘亚珲, 赵倩,

基于聚类经验模态分解的CNN-LSTM超短期电力负荷预测

[J]. 电网技术, 2021, 45 (11): 4444- 4451.

URL     [本文引用: 1]

Liu Y H , Zhao Q ,

Ultra-short-term Power Load Forecasting Method Based on Cluster Empirical Mode Decomposition of CNN-LSTM

[J]. Power System Technology, 2021, 45 (11): 4444- 4451.

URL     [本文引用: 1]

孙少龙, 魏云捷, 汪寿阳,

基于分解-聚类-集成学习的汇率预测方法

[J]. 系统工程理论与实践, 2021, 42 (3): 664- 677.

URL     [本文引用: 1]

Sun S L , Wei Y J , Wang S Y ,

Exchange Rates Forecasting with Decomposition-clustering-ensemble Learning Approach

[J]. Systems Engineering — Theory & Practice, 2021, 42 (3): 664- 677.

URL     [本文引用: 1]

石雪涛, 朱帮助,

基于相空间重构和最小二乘支持向量回归模型参数同步优化的碳市场价格预测

[J]. 系统科学与数学, 2017, 37 (2): 562- 572.

URL     [本文引用: 1]

Shi X T , Zhu B Z ,

Carbon Price Forecasting Based on Phase Space Reconstruction and Least Square Support Vector Regression

[J]. Journal of Systems Science and Mathematical Sciences, 2017, 37 (2): 562- 572.

URL     [本文引用: 1]

杨星, 梁敬丽, 蒋金良, 米君龙,

多标度分形特征下碳排放权价格预测算法

[J]. 控制理论与应用, 2018, 35 (2): 224- 231.

URL     [本文引用: 2]

Yang X , Liang J L , Jiang J L , Mi J L ,

Price Forecasting Algorithm of Carbon Emission Rights Under Multiscale Fractal Characteristics

[J]. Control Theory & Applications, 2018, 35 (2): 224- 231.

URL     [本文引用: 2]

张晨, 杨仙子,

基于多频组合模型的中国区域碳市场价格预测

[J]. 系统工程理论与实践, 2016, 36 (12): 3017- 3025.

DOI      [本文引用: 1]

Zhang C , Yang X Z ,

Forecasting of China's Regional Carbon Market Price Based on Multi-frequency Combined Model

[J]. Systems Engineering — Theory & Practice, 2016, 36 (12): 3017- 3025.

DOI      [本文引用: 1]

张雯, 吴志彬, 徐玖平, (2021). 基于EMD-PSO-LSSVM的碳排分解集成预测方法[J/OL]. 控制与决策. doi: 10.13195/j.kzyjc.2020.1787.

[本文引用: 1]

Zhang W, Wu Z B, Xu J P, (2021). A Decomposition-integration Forecasting Method of Carbon Emission Based on EMD-PSO-LSSVM[J/OL]. Control and Decision. doi: 10.13195/j.kzyjc.2020.1787.

[本文引用: 1]

朱帮助, 魏一鸣,

基于GMDH-PSO-LSSVM的国际碳市场价格预测

[J]. 系统工程理论与实践, 2011, 31 (12): 2264- 2271.

DOI      [本文引用: 1]

Zhu B Z , Wei Y M ,

Carbon Price Prediction Based on Integration of GMDH, Particle Swarm Optimization and Least Squares Support Vector Machines

[J]. Systems Engineering — Theory & Practice, 2011, 31 (12): 2264- 2271.

DOI      [本文引用: 1]

赵康宁, 蒲天骄, 王新迎, 李烨,

基于改进贝叶斯神经网络的光伏出力概率预测

[J]. 电网技术, 2019, 43 (12): 4377- 4386.

URL     [本文引用: 1]

Zhao K N , Pu T J , Wang X Y , Li Y ,

Probabilistic Forecasting for Photovoltaic Power Based on Improved Bayesian Neural Network

[J]. Power System Technology, 2019, 43 (12): 4377- 4386.

URL     [本文引用: 1]

Adekoya O B ,

Predicting Carbon Allowance Prices with Energy Prices: A New Approach

[J]. Journal of Cleaner Production, 2021, 282, 124519.

DOI      [本文引用: 1]

Anand A , Suganthi L ,

Forecasting of Electricity Demand by Hybrid ANN-PSO Models

[J]. International Journal of Energy Optimization and Engineering (IJEOE), 2017, 6 (4): 66- 83.

DOI      [本文引用: 1]

Hao Y , Tian C S ,

A Hybrid Framework for Carbon Trading Price Forecasting: The Role of Multiple Influence Factor

[J]. Journal of Cleaner Production, 2020, 262, 120378.

DOI      [本文引用: 1]

Huang Y M , Dai X Y , Wang Q W , Zhou D Q ,

A Hybrid Model for Carbon Price Forecasting Using GARCH and Long Short-Term Memory Network

[J]. Applied Energy, 2021, 285, 116485.

DOI      [本文引用: 1]

Kim T Y , Cho S B ,

Predicting Residential Energy Consumption Using CNN-LSTM Neural Networks

[J]. Energy, 2019, 182, 72- 81.

DOI     

Lu H F , Ma X , Huang K , Azimi M ,

Carbon Trading Volume and Price Forecasting in China Using Multiple Machine Learning Models

[J]. Journal of Cleaner Production, 2020, 249, 119386.

DOI     

Shahid F , Zameer A , Muneeb M ,

A Novel Genetic LSTM Model for Wind Power Forecast

[J]. Energy, 2021, 223, 120069.

DOI      [本文引用: 1]

Sun W , Zhang C ,

Analysis and Forecasting of the Carbon Price Using Multi-Resolution Singular Value Decomposition and Extreme Learning Machine Optimized by Adaptive Whale Optimization Algorithm

[J]. Applied Energy, 2018, 231, 1354- 1371.

DOI      [本文引用: 1]

Tang L , Wang H H , Li L , Yang K T , Mi Z F ,

Quantitative Models in Emission Trading System Research: A Literature Review

[J]. Renewable and Sustainable Energy Reviews, 2020, 132, 110052.

DOI      [本文引用: 1]

Wang J J , Cui Q , Sun X ,

A Novel Framework for Carbon Price Prediction Using Comprehensive Feature Screening, Bidirectional Gate Recurrent Unit and Gaussian Process Regression

[J]. Journal of Cleaner Production, 2021, 314, 128024.

DOI      [本文引用: 1]

Xie G , Shangguan A Q , Fei R , Ji W J , Ma W Q , et al.

Motion Trajectory Prediction Based on A CNN-LSTM Sequential Model

[J]. Science China Information Sciences, 2020, 63 (11): 1- 21.

[本文引用: 1]

Xiong S H , Wang C F , Fang Z M , Ma D ,

Multi-Step-Ahead Carbon Price Forecasting Based on Variational Mode Decomposition and Fast Multi-Output Relevance Vector Regression Optimized by The Multi-Objective Whale Optimization Algorithm

[J]. Energies, 2019, 12 (1): 147.

DOI      [本文引用: 1]

Yang J H , Dou W ,

A New Prediction Method of Gold Price: EMD-PSO-SVM

[J]. Journal of Software, 2014, 9 (1): 195.

[本文引用: 1]

Zhang J , Li D , Hao Y , Tan Z ,

A Hybrid Model Using Signal Processing Technology, Econometric Models and Neural Network for Carbon Spot Price Forecasting

[J]. Journal of Cleaner Production, 2018, 204, 958- 964.

DOI      [本文引用: 1]

Zhang W , Li J , Li G X , Guo S C ,

Emission Reduction Effect and Carbon Market Efficiency of Carbon Emissions Trading Policy in China

[J]. Energy, 2020, 196, 117117.

DOI      [本文引用: 2]

Zhang X , Zhang X X , Wei Z Q ,

Carbon Price Forecasting Based on Multi-Resolution Singular Value Decomposition and Extreme Learning Machine Optimized by the Moth-Flame Optimization Algorithm Considering Energy and Economic Factors

[J]. Energies, 2019, 12 (22): 4283.

DOI      [本文引用: 1]

Zhang Y F , Li S , Luo T Y , Gao J ,

The Effect of Emission Trading Policy on Carbon Emission Reduction: Evidence from An Integrated Study of Pilot Regions in China

[J]. Journal of Cleaner Production, 2020, 265, 121843.

DOI     

Zhao J F , Mao X , Chen L J ,

Speech Emotion Recognition Using Deep 1D & 2D CNN LSTM Networks

[J]. Biomedical Signal Processing and Control, 2019, 47, 312- 323.

DOI      [本文引用: 1]

Zhou K , Li Y ,

An Empirical Analysis of Carbon Emission Price in China

[J]. Energy Procedia, 2018, 152, 823- 828.

DOI      [本文引用: 1]

Zhu B , Ye S , Wang P , He K , Zhang T , et al.

A Novel Multiscale Nonlinear Ensemble Leaning Paradigm for Carbon Price Forecasting

[J]. Energy Economics, 2018, 70, 143- 157.

DOI      [本文引用: 1]

Zhu B Z , Han D , Wang P , Wu Z C , Zhang T , et al.

Forecasting Carbon Price Using Empirical Mode Decomposition and Evolutionary Least Squares Support Vector Regression

[J]. Applied Energy, 2017, 191, 521- 530.

DOI      [本文引用: 1]

/

〈 〉