1 引言
决策行为往往伴随着不确定性. 在某些情况下, 人们可以基于历史数据或理论推导了解不确定性前景的概率分布, 如购买福利彩票. 而在更常见的情况下, 例如进行实业投资、证券投资时, 由于经济环境复杂多变, 这些决策在未来的收益概率往往难以得到准确的估计. Ellsberg (1961)的双色球实验指出, 更多的决策者可能更偏好于承受已知概率的风险, 而非未知概率分布的不确定性. 这一选择体现出风险(已知概率)和不确定性(未知概率)之间的区别, Ellsberg把后者命名为暧昧性(ambiguity).
大量的实验文章证实了这种暧昧厌恶(ambiguity aversion)现象的普遍存在(例如, Becker and Brownson (1964), Curley and Yates (1989), Slovic and Tversky (1974)). 由于这种现象无法被期望效用(expected utility)理论所解释, 因而行为决策理论此后也不断发展, 以刻画投资者的这种暧昧厌恶特征, 例如, 最大最小期望效用(Gilboa and Schmeidler (1989)), Choquet期望效用(Schmeidler (1989)), 光滑暧昧厌恶模型(Klibanoff et al. (2005)), 以及Segal (1987, 1990), Bewley (2002), Ergin and Gul (2009), Gul and Pesendorfer (2014)等提出的效用模型.
而现实世界每时每刻都可能产生新的信息, 因此实际决策环境往往是动态而非静态, 需要考虑对信息的学习. 在风险环境中, 由于先验概率分布已知, 决策者可以使用贝叶斯规则进行信念更新, 而在暧昧环境中, 先验概率分布未知, 贝叶斯法则难以适用, 这就提出了一个问题: 当有关暧昧前景的新信息出现时, 决策者的信念和态度会如何改变? 过去的理论文献将静态暧昧厌恶决策模型拓展至多期, 提出了不同的信念更新规则(Gilboa and Schmeidler (1993), Epstein and Schneider (2003, 2007), Epstein (2006), Hanany and Klibanoff (2009)), 并指出当暧昧前景的信息越来越多时, 未知概率会变得越来越"已知", 暧昧性会逐渐降低, 极限状态下暧昧性会消失, 随之决策者行为也会逐渐向期望效用收敛(Marinacci (2002), Epstein and Schneider (2007), Marinacci and Massari (2019)). 但是在暧昧环境中进行信息学习的实验证据却较为缺乏, 现有实验文献对于信息对决策的影响也莫衷一是. Trautmann and Zeckhauser (2013)的实验结果表明: 决策者经常避免在不确定的环境中进行决策, 并且无法认识到学习带来的好处, 因此信息对于决策者的影响有限, 而Ert and Trautmann (2014), Baillon et al. (2018)的实验则肯定了信息对于决策者行为的影响, 这种不一致的结论促使我们考虑信息对于不同决策者影响的异质性. 因此, 本文旨在从实验的角度检验信息对决策的影响以及这种影响在不同的决策者之间的异质性.
本文对经典双色球实验(Ellsberg (1961))进行了两阶段拓展, 主要包括两个部分: 第一部分是静态拓展, 暧昧罐子的设置与经典双色球实验保持一致, 改变风险罐子中黑球与红球的比例, 并通过决策者在一系列风险罐子和暧昧罐子间的选择反推出决策者的暧昧厌恶程度; 第二部分是动态实验, 风险罐子的设置与经典双色球实验保持一致, 但是向决策者提供暧昧罐子中球的分布的信息, 观察决策者的选择与经典双色球选择中的区别. 实验结果表明: 1)静态Ellsberg双色球实验中, 多数参与者体现出了暧昧厌恶; 2)抽球信息改变了一部分参与者在静态实验中表现出的对于暧昧性的厌恶态度; 3)在静态实验中体现出的暧昧厌恶程度越高的参与者, 抽球信息对于他们决策的影响可能越小, 也就是说, 暧昧厌恶程度高的决策者表现出对信息的低信心.
实验中常用的度量暧昧厌恶的方法是基于Ellsberg双色球实验的衍生, 即, 从个体在风险和暧昧前景之间的二选一决策中反推出他们的暧昧偏好, 或测量对风险和暧昧彩票的支付意愿(例如, Dimmock, Kouwenberg and Mitchell et al. (2016), Dimmock, Kouwenberg and Wakker, (2016), Trautmann et al. (2011)). 但是, 大多数实验文献仅仅将被试分为暧昧厌恶、暧昧中性和暧昧喜好三类, 却没有对暧昧厌恶程度的不同进行进一步的探讨. 而且, 以往有关暧昧厌恶的实验文献往往主要关注决策者静态决策(例如, Becker and Brownson (1964), Curley and Yates (1989), Slovic and Tversky (1974))或动态信息学习(例如, Trautmann and Zeckhauser (2013), Ert and Trautmann (2014), Baillon et al. (2018))的其中一方面, 而没有将决策者在静态环境下的暧昧厌恶程度与动态学习相结合. 在本文实验设置中, 我们没有将所有暧昧厌恶的决策者视为同质的, 而是进一步将暧昧厌恶的被试者按照暧昧厌恶程度划分成不同的子样本, 这使得我们可以分别观察子样本中的决策者在面对新信息时的不同反应, 从而将个体的静态暧昧厌恶与他们的信息学习过程联系起来. 我们的实验结果表明, 在静态实验中体现出的暧昧厌恶程度越高的参与者, 抽球信息对于他们决策的影响可能越小, 他们对于新信息的信任程度可能越低.
本文剩余内容包括: 第2节描述了实验内容, 第3节总结实验结果并进行解释, 第4节总结全文.
2 实验
经典的Ellsberg双色球实验可以简化为: 假设有两个装着黑球或者红球的罐子(罐子1和罐子2), 每个罐子里都有100个球, 其中:
罐子1: 黑球红球数量未知, 红球可能有0到100个;
罐子2: 黑球红球各50个.
黑球和红球的形状、大小、质量等特征都相同, 仅有颜色的差异, 参与者在进行抽球时看不到罐子中的球. 要求参与者选择一个罐子从中抽球, 如果从罐子中抽中某个颜色的球(比如红球)可以获得奖励(比如100美元), 抽中其他颜色的球(比如黑球)则没有奖励. 那么参与者会选择参与以下哪个抽奖:
A: 从罐子1中抽球
B: 从罐子2中抽球
经验数据表明1, 大部分的参与者会选择从罐子2中抽球, 这体现出更多的决策者更偏好于承受已知概率的风险, 而非未知概率分布的不确定性, 这种偏好被称为暧昧厌恶(ambiguity aversion).
1Camerer and Weber (1992)的3.1节中总结了此前的文献中有关Ellsberg双色球实验的经验证据.
本文的实验则基于Ellsberg双色球实验进行改造, 主要分为两个部分: 第一部分通过改变罐子2中球的组成度量参与者的暧昧厌恶程度; 第二部分通过改变罐子1抽球的步骤判断被试者主观信念的改变, 从而得到不同暧昧厌恶程度的被试在更新主观信念时的异质性. 具体实验问卷可在附录中查看.
2.1 第一部分
第一部分实验的目的在于测试参与者的暧昧厌恶程度, 并将参与者按照暧昧厌恶程度分组. 关于暧昧厌恶程度的度量, Dimmock, Kouwenberg and Mitchell et al. (2016), Dimmock, Kouwenberg and Wakker, (2016)采用匹配概率(matching probability) 度量实验参与者的暧昧厌恶态度, 也就是令决策者在具有暧昧性的前景和具有不同确定概率中奖的前景之间进行选择, 从而得到对于参与者来说与暧昧性前景无差异的确定中奖概率
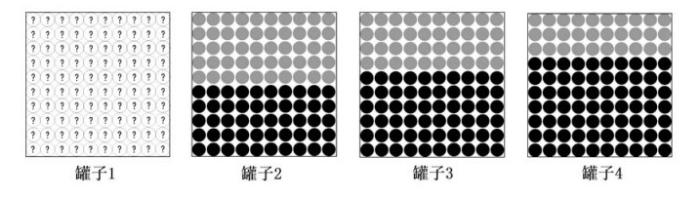
本文参考了这一度量指标2, 给出4个装着黑球或者红球的不透明罐子, 每个罐子里都有100个球, 黑球和红球的形状、大小、质量等特征都相同, 仅有颜色的差异. 如图 1所示, 罐子1是具有暧昧性的罐子, 其余3个罐子明确给出罐子中黑球与红球的个数(其中红球用灰色表示):
2Trautmann et al. (2011)指出, 实验中常用的度量决策者暧昧厌恶态度的方法有两种, 第一种是让受试者在具有暧昧性的和有风险的前景之间直接做出选择, 即匹配概率法; 第二种是直接询问受试者为暧昧性抽奖付费的意愿WTP (willingness to pay). WTP虽然提供了个体层面的暧昧厌恶的量化指标, 但其会受到损失厌恶的影响因而倾向于高估暧昧厌恶程度. 如果让受试者在具有不确定性的抽奖和不同的确定收益之间进行选择, 从而得到确定性等价CE (certainty equivalent)可以减少损失厌恶的影响. 但考虑到将不确定性前景与确定收益相比较涉及到对于不确定性前景的估值, 相比匹配概率的认知复杂程度更高, 因此本文令决策者在暧昧性罐子与不同的风险罐子之间进行比较, 从而得出暧昧厌恶程度.
图1
罐子1: 黑球红球数量未知, 红球可能有0到100个;
罐子2: 红球与黑球各50个;
罐子3: 红球40个, 黑球60个;
罐子4: 红球30个, 黑球70个.
第一部分实验包括3个问题, 分别将罐子1与罐子2、3、4对比, 询问参与者: 如果从所选罐子中抽出红球可以获得奖励100000元, 更愿意从哪个罐子中进行抽奖3? 参与者首次选择罐子1时, 其对应题目序号即为暧昧厌恶等级, 并且跳过这一部分接下来的问题. 如果参与者始终没有选择罐子1, 则其对应的暧昧厌恶等级为4.
3经典的Ellsberg实验中, 受试者是可以自行选择下注的颜色的, 但本文直接指定了红色, 一方面是考虑到调查方式为在线问卷, 红色相对于黑色更加明显, 便于受试者理解实验; 另一方面, Abdellaoui et al. (2011), Fox and Tversky (1998)的实验表明, 受试者对于在两种颜色上进行实验并没有显著偏好, 这里直接采用抽红球的方式, 也是为了使实验更加简单, 便于理解.
具体来看, 这部分问卷的问题为:
1.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖?
A. 罐子1 (
4括号中的内容对被试者不可见, 这里只是为了阐明暧昧厌恶分级依据.
B. 罐子2 (
2.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖?
A. 罐子1 (
B. 罐子3 (
3.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖?
A. 罐子1 (
B. 罐子4 (
从罐子2到罐子4, 红球的比例逐步下降, 因此从中抽出红球的概率逐渐降低. 从参与者首次选择罐子1的问题序号中可以看出, 当风险罐子中红球比例为多少时, 参与者更愿意从罐子1中抽球, 或者两个罐子至少是无差异的. 首次选择罐子1的序号越大, 参与者为了避免暧昧性抽奖而愿意接受的抽中红球的概率就越低, 对于暧昧性的厌恶程度相应地就越高. 所以首次选择罐子1的问题序号, 可以反映出其暧昧厌恶程度, 如果参与者始终不选择罐子1, 则说明参与者暧昧厌恶程度非常高. 举例来看, 当罐子1与罐子2进行对比时, 这就是经典的Ellsberg双色球实验, 此时如果参与者选择具有暧昧性的罐子1, 则表示参与者对于暧昧性并不厌恶, 将其暧昧厌恶程度记为1, 如果参与者选择罐子2, 则进行下一个问题.
请注意, 在这一部分实验中, 只有暧昧厌恶程度为1 (表示对暧昧性持中立态度或暧昧偏好)的一组样本在经典Ellsberg双色球实验中选择了具有暧昧性的罐子1, 其他3组参与者都选择了风险罐子2, 他们的行为体现出了暧昧厌恶.
2.2 第二部分
第二部分实验的目的在于, 向参与者提供有关暧昧性罐子1的信息, 并观察新信息是否会改变参与者(暧昧厌恶的3组参与者)的选择, 以及不同暧昧厌恶的程度参与者决策有什么区别.
在第一部分给出的4个罐子中, 现在只关注罐子1和2, 每个罐子里都有100个球(红球或黑球), 黑球和红球的形状、大小、质量等特征都相同, 仅有颜色的差异, 参与者在进行抽球时看不到罐子中的球. 要求参与者选择一个罐子从中抽球, 如果从罐子中抽中指定颜色的球可以获得奖励(比如100000元), 抽中其他颜色的球则没有奖励. 其中,
罐子1: 黑球红球数量未知, 红球可能有0到100个;
罐子2: 黑球红球各50个.
首先, 允许参与者从罐子1中进行1次放回式抽球(可以观察到所抽出的球的颜色), 假设抽出了红色球, 询问参与者更愿意参加以下哪一个抽奖5:
5请注意, 这里把抽球过程放在了决策者进行选择之前, 而非直接让决策者在以下两个选项中进行选择: A.从罐子1中抽一次球之后放回(可以看到所抽的球的颜色), 再选择一个颜色(红/黑), 从罐子1中抽球, 如果抽到所选定的颜色的球, 则获得奖励100000元, 否则没有奖励. B.选择一个颜色(红/黑), 从罐子2中抽球, 如果抽到所选定的颜色的球, 则获得奖励100000元, 否则没有奖励. 比较两种实验设置, 后者是把抽球的步骤内化在了选项里面. 对于后一种实验设置来说, 如果决策者选择A选项, 只需要保证选择与第一次抽球时相同的颜色下注, 这样的策略下所获得奖励的概率不低于选项B, 因为
A. 如果从罐子1中抽到红球, 则获得奖励100000元, 否则没有奖励
B. 如果从罐子1中抽到黑球, 则获得奖励100000元, 否则没有奖励
C. 如果从罐子2中抽到红球, 则获得奖励100000元, 否则没有奖励
D. 如果从罐子2中抽到黑球, 则获得奖励100000元, 否则没有奖励
接下来, 允许参与者从罐子1中试抽10次球(每次抽球之后再放回罐子中), 在试抽球后确定一个颜色, 然后选择从某一罐子中抽球. 询问参与者更愿意参加以下哪一个抽奖:
A. 罐子1 (即如果从罐子1中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
B. 罐子2 (即如果从罐子2中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
在这一部分实验中, 罐子1中的黑球红球依然是个数未知, 如果直接让参与者选择从一个罐子中抽球, 那么具有暧昧厌恶特征的参与者会选择罐子2, 但是如果允许参与者通过抽球实验的方式了解更多罐子1的信息, 这就存在了学习过程, 即从每次抽球的结果来推测其中的不同颜色球的比例. 如果通过抽球实验可以判断出罐子1中某些颜色的球更多, 显然选择从罐子1中抽对应颜色的球是更有优势的, 这也是决策者可能会选择罐子1中抽球的原因. 如果参与者相对于可能通过抽球获得的信息来说, 更加厌恶这种未知概率分布的不确定性, 并不愿意进行尝试, 那么就会选择罐子2进行抽球.
3 实验结果
3.1 参与者特征
本文实验采用在线问卷调查的形式进行(使用问卷星平台), 问卷调查共收回答卷364份, 将作答时间过短的答卷视为无效, 共有281份有效答卷6. 参与者中有104名男性, 177名女性,
6投放问卷时与另一组研究人员合作, 接受过经管类教育的参与者会填写两部分问卷(本文的与另一组研究人员的), 这部分参与者作答时间低于3分钟的视为无效, 未接受过经管类教育的参与者仅填写本文的问卷, 这部分参与者作答时间低于1分钟的视为无效.
3.2 实验结果
第一部分实验主要结果为: 1)大部分参与者在静态决策中体现出暧昧厌恶的态度; 2)将参与者按照暧昧厌恶程度划分为4组, 其中第一组的选择体现出了暧昧偏好, 其他三组则体现出了暧昧厌恶7。
7为了更精细地度量参与者的暧昧厌恶程度, 问卷投放时还增加了45个红球55个黑球的罐子, 以供参与者选择, 但在分组时将45个红球55个黑球的罐子和40个红球60个黑球罐子的选择合并处理: 将45个红球55个黑球的罐子与暧昧罐子1进行比较, 选择罐子1的参与者暧昧厌恶程度为2, 选择前者的则继续在40个红球60个黑球的罐子与暧昧罐子1之间进行选择, 选择罐子1的参与者暧昧厌恶程度也为2, 选择风险罐子的则继续回答下一题.
第一部分实验的详细结果见表 1, 可以看出在经典的Ellsberg双色球实验中(直接将罐子1与罐子2进行对比), 有
表1 样本的暧昧厌恶态度
| 暧昧厌恶态度 | 全样本 | 男 | 女 | 经管类 | 非经管类 |
| 1 (暧昧偏好) | 37 | 15 | 22 | 15 | 22 |
| (13.17%) | (14.42%) | (12.43%) | (7.69%) | (25.58%) | |
| 2 | 79 | 29 | 50 | 57 | 22 |
| (28.11%) | (27.88%) | (28.25%) | (29.23%) | (25.58%) | |
| 3 | 85 | 28 | 57 | 64 | 21 |
| (30.25%) | (26.92%) | (32.20%) | (32.82%) | (24.42%) | |
| 4 | 80 | 32 | 48 | 59 | 21 |
| (28.47%) | (30.77%) | (27.12%) | (30.26%) | (24.42%) | |
| 合计 | 281 | 104 | 177 | 195 | 86 |
| (100%) | (100%) | (100%) | (100%) | (100%) |
注: 括号内表示样本所占比例.
按照暧昧厌恶程度可以将参与者分为四个组, 暧昧偏好的组有37人, 占总有效答卷的
第二部分实验的主要结果为: 1)有关于罐子1的信息会改变部分暧昧厌恶的参与者对于风险和暧昧性的选择; 2)总体来看, 相比较于抽1次球, 抽10次球后, 改变选择的参与者比例更高; 3)在静态环境中体现出的暧昧厌恶程度越高的参与者, 抽球信息对于他们决策的影响可能越小, 他们的选择表现出的对于新信息的信心较低.
暧昧厌恶的参与者(共244人)在第一部分罐子1与罐子2的对比中, 均选择了从罐子2 (风险罐子)中抽奖, 而在观察到从罐子1中抽出红球后, 有
表2 抽出红球后暧昧厌恶的参与者的选择
| 参与者的选择 | 暧昧厌恶者 | 男 | 女 | 经管类 | 非经管类 | |
| 罐子1 | 红球 | 91 | 30 | 61 | 68 | 23 |
| (37.30%) | (33.71%) | (39.35%) | (37.78%) | (35.94%) | ||
| 黑球 | 16 | 7 | 9 | 8 | 8 | |
| (6.56%) | (7.87%) | (5.81%) | (4.44%) | (12.50%) | ||
| 罐子2 | 红球 | 120 | 46 | 74 | 90 | 30 |
| (49.18%) | (51.69%) | (47.74%) | (50.00%) | (46.88%) | ||
| 黑球 | 17 | 6 | 11 | 14 | 3 | |
| (6.97%) | (6.74%) | (7.10%) | (7.78%) | (4.69%) | ||
| 合计 | 244 | 89 | 155 | 180 | 64 | |
| (100%) | (100%) | (100%) | (100%) | (100%) | ||
注: 括号内表示样本所占比例.
当允许参与者在观察到抽出的球后先挑选一个颜色, 再在两个罐子之间挑一个进行抽奖时, 抽球次数对于参与者的选择也会有一定的影响, 表 3给出了抽1次球与抽10次球后选择从罐子1中抽奖的参与者人数及比例. 总体来看, 相比较抽1次球, 抽10次球时会有更多的参与者选择具有暧昧性的罐子, 随着抽球次数的增加, 参与者对于罐子1的了解也会增加, 因此更愿意选择具有暧昧性的罐子, 但是将经管类样本与未接受过经管类教育的样本对比, 这种现象在接受过经管类相关教育的样本中比较明显, 而非经管类样本并没有这个倾向, 可能是接受过经管类教育的参与者, 更能意识到信息学习的作用.
表3 选择罐子1的暧昧厌恶参与者人数与比例
| 暧昧厌恶者 | 男 | 女 | 经管类 | 非经管类 | |
| 抽1次球 | 107 | 37 | 70 | 76 | 31 |
| (43.85%) | (41.57%) | (45.16%) | (42.22%) | (48.44%) | |
| 抽10次球 | 149 | 53 | 96 | 119 | 30 |
| (61.07%) | (59.55%) | (61.94%) | (66.11%) | (46.88%) |
注: 括号内表示样本所占比例.
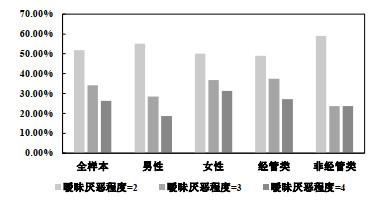
把3个暧昧厌恶的子样本分组来看, 可以发现, 参与者的选择与他们的暧昧厌恶程度有一定的关系. 如表 4所示, 观察到从罐子1中抽出红球后, 在暧昧厌恶程度较低(等级为2)的子样本中,
表4 抽出红球后暧昧厌恶参与者选择"红1"的概率
| 暧昧厌恶程度 | 暧昧厌恶者 | 男 | 女 | 经管类 | 非经管类 |
| 2 | 51.90% | 55.17% | 50.00% | 49.12% | 59.09% |
| 3 | 34.12% | 28.57% | 36.84% | 37.50% | 23.81% |
| 4 | 26.25% | 18.75% | 31.25% | 27.12% | 23.81% |
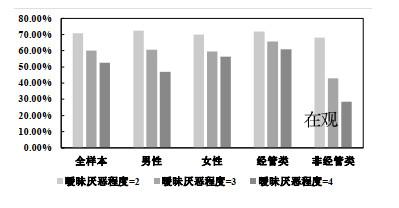
表5 抽10次球后暧昧厌恶参与者选择罐子1的比例
| 暧昧厌恶程度 | 暧昧厌恶者 | 男 | 女 | 经管类 | 非经管类 |
| 2 | 70.89% | 72.41% | 70.00% | 71.93% | 68.18% |
| 3 | 60.00% | 60.71% | 59.65% | 65.63% | 42.86% |
| 4 | 52.50% | 46.88% | 56.25% | 61.02% | 28.57% |
图2
图3
3.3 讨论
Ellsberg双色球实验告诉我们, 风险和暧昧性可以区分开来. 从我们的实验也可以看出, 很多参与者都表现出了暧昧厌恶的特征, 在两个罐子中更倾向于从纯风险罐子2中抽球. 然而, 第二部分实验中, 允许参与者在做出选择之前抽球, 也就是多获取一些关于罐子1的信息, 就会使相当一部分在静态选择中体现出暧昧厌恶的参与者选择从罐子1中抽球. 这种偏好的变化说明, 在观察到从罐子1中抽出红球后, 他们认为从罐子1中抽球可能可以使他们获得某种优势, 所以在可以进行抽球实验的条件下选择暧昧性的罐子.
而不同的决策者对于信息的态度是不同的, 暧昧厌恶程度更高的决策者在面对有利信息时似乎更加不为所动, 而暧昧厌恶程度较低的决策者则更有可能因为信息显示有利而改变之前的决策, 这体现出信息学习在不同类决策者之间的异质性.
另外, 本文的实验也存在一些不足: 1)考虑到线上问卷的回收效率, 本文实验只进行了1次, 10次抽球的实验, 没有进行更多其他次数抽球对于参与者的决策影响; 2)样本分布中, 接受过经管类教育的参与者人数远远高于未接受过经管类教育的参与者, 样本分布不够均匀, 因此只能将接受过经管类教育的参与者视为同质性更强的样本作为对于结果的进一步检验, 而不能够将两类参与者进行对比得到其他比较可靠的结果; 3)实验是线上问卷的形式进行, 而且没有考虑到参与者所获得的激励对于选择的影响, 因此可能需要再在更加专业的实验室中进行, 以保证结果的可靠性.
4 结语
本文首先提出了一个包含两部分内容的思想实验, 第一部分测试参与者的暧昧厌恶程度, 第二部分在Ellsberg双色球实验的基础上增加了抽球条件, 我们发现, 在增加抽球条件后, 一些决策者改变了之前的选择, 从选择纯风险的罐子2转而选择具有暧昧性的罐子1, 并且暧昧厌恶程度较低的参与者更有可能改变之前的选择.
在增加了抽球条件后, 决策者可以通过观察所抽出的球进行学习, 推测罐子中的球的比例, 而面对同样的信息, 暧昧厌恶程度较高的决策者对于信息似乎显示出更低的信心, 信息改变他们决策的概率较低. 而暧昧厌恶程度较轻的决策者则更有可能对信息持有相当高的信心, 较为有利的信息可以使很大比例的决策者从选择风险前景转向选择暧昧前景, 这改变了他们在静态决策中的选择.
在具有暧昧性的环境中, 决策者行为的目标函数与风险环境中不同, 因此与风险环境中的决策适用的决策理论框架不同. 本文对于暧昧环境下的信息更新过程的讨论有助于将博弈论拓展到更为复杂的不确定性环境中, 考虑暧昧环境中决策者的信念更新模式, 这对于解释不确定环境下的市场均衡也会有一定的参考价值. 暧昧厌恶程度越高的人, 在信息学习过程中越不信任新信息, 这一部分可以在接下来进行进一步的研究, 可能有助于解释一些反应不足的金融异象.
附录
附录: 抽奖偏好实验
请问您是否为经管类专业学生(包含已毕业) [单选题] *
A. 是
B. 否
第一部分
假设有5个装着红球或者黑球的不透明罐子, 每个罐子里都有100个球, 红球与黑球的形状、大小、质量等特征都相同, 仅有颜色的差异. 其中:
罐子1: 红球黑球数量不知道, 红球可能有0到100个;
罐子2: 红球与黑球各50个;
罐子3: 红球45个, 黑球55个;
罐子4: 红球40个, 黑球60个;
罐子5: 红球30个, 黑球70个.
1.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖? [单选题]
A. 罐子1 (黑球红球数量不知道, 红球可能有0到100个)
B. 罐子2 (黑球红球各50个)
2.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖? [单选题]
A. 罐子1 (黑球红球数量不知道, 红球可能有0到100个)
B. 罐子3 (红球45个, 黑球55个)
3.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖? [单选题]
A. 罐子1 (黑球红球数量不知道, 红球可能有0到100个)
B. 罐子4 (红球40个, 黑球60个)
4.如果从所选罐子中抽出红球可以获得奖励100000元, 那么下面两个罐子相比较, 你更愿意从哪个罐子中进行抽奖? [单选题]
A. 罐子1 (黑球红球数量不知道, 红球可能有0到100个)
B. 罐子5 (红球30个, 黑球70个)
第二部分
5.现在允许你从罐子1中试抽一次球(之后放回罐子中), 假设你从中抽出了红球. 此时, 下面几个抽奖你更愿意参加哪一个? 其中,
罐子1: 黑球红球数量不知道, 红球可能有1
罐子2: 黑球红球各50个. [单选题]
A. 如果从罐子1中抽到红球, 则获得奖励100000元, 否则没有奖励
B. 如果从罐子1中抽到黑球, 则获得奖励100000元, 否则没有奖励
C. 如果从罐子2中抽到红球, 则获得奖励100000元, 否则没有奖励
D. 如果从罐子2中抽到黑球, 则获得奖励100000元, 否则没有奖励
6.现在允许你从罐子1中试抽一次球(之后不放回罐子中), 假设你从中抽出了红球. 此时, 下面几个抽奖你更愿意参加哪一个? 其中,
罐子1: 黑球红球数量不知道, 红球可能有1
A. 如果从罐子1中抽到红球, 则获得奖励100000元, 否则没有奖励
B. 如果从罐子1中抽到黑球, 则获得奖励100000元, 否则没有奖励
C. 如果从罐子2中抽到红球, 则获得奖励100000元, 否则没有奖励
D. 如果从罐子2中抽到黑球, 则获得奖励100000元, 否则没有奖励
7.现在允许你从罐子1中试抽10次球(每次抽球之后再放回罐子中), 在试抽球后确定一个颜色, 然后选择从某一罐子中抽球. 在选择罐子时, 下面几个抽奖你更愿意参加哪一个? 其中,
罐子1: 黑球红球数量不知道, 红球可能有1
罐子2: 黑球红球各50个. [单选题]
A. 罐子1 (即如果从罐子1中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
B. 罐子2 (即如果从罐子2中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
8.现在允许你从罐子1中试抽10次球(每次抽球之后不放回罐子中), 在试抽球后确定一个颜色, 然后选择从某一罐子中抽球. 在选择罐子时, 下面几个抽奖你更愿意参加哪一个? 其中, 初始时
罐子1: 黑球红球数量不知道, 红球可能有1
罐子2: 黑球红球各50个. [单选题]
A. 罐子1 (即如果从罐子1中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
B. 罐子2 (即如果从罐子2中抽到预先指定颜色的球, 则获得奖励100000元, 否则没有奖励)
9.请问您目前是否持有以下资产或从事相关交易? [多选题]
A. 股票
B. 证券基金
C. 货币市场基金(比如余额宝, 零钱通等)
D. 金融衍生品(期权, 期货等)
E. 银行存款
F. 其他
10.您的性别[单选题]
A. 男
B. 女
参考文献
The Rich Domain of Uncertainty: Source Functions and Their Experimental Implementation
[J].
The Effect of Learning on Ambiguity Attitudes
[J].
What Price Ambiguity? Or the Role of Ambiguity in Decision-Making
[J].
Knightian Decision Theory. Part Ⅰ
[J].
Recent Developments in Modeling Preferences?: Uncertainty and Ambiguity
[J].
An Empirical Evaluation of Descriptive Models of Ambiguity Reactions in Choice Situations
[J].
Ambiguity Aversion and Household Portfolio Choice Puzzles: Empirical Evidence
[J].
Ambiguity Attitudes in a Large Representative Sample
[J].
Risk, Ambiguity, and the Savage Axioms
[J].
An Axiomatic Model of Non-Bayesian Updating
[J].
Recursive Multiple-Priors
[J].
Learning under Ambiguity
[J].
A Theory of Subjective Compound Lotteries
[J].
Sampling Experience Reverses Preferences for Ambiguity
[J].
A Belief-Based Account of Decision under Uncertainty
[J].
Maxmin Expected Utility with Nonunique Prior
[J].
Updating Ambiguous Beliefs
[J].
Expected Uncertain Utility Theory
[J].
Updating Ambiguity Averse Preferences
[J].
A Smooth Model of Decision Making under Ambiguity
[J].
Learning from Ambiguous Urns
[J].
Learning from Ambiguous and Misspecified Models
[J].
Subjective Probability and Expected Utility without Additivity
[J].
The Ellsberg Paradox and Risk Aversion?: An Anticipated Utility Approach
[J].
Two-Stage Lotteries without the Reduction Axiom
[J].
Who Accepts Savage's Axiom?
[J].
Preference Reversals for Ambiguity Aversion
[J].
Shunning Uncertainty: The Neglect of Learning Opportunities
[J].