1 引言
党的十八大以来, 随着我国生态文明建设不断推进, 绿色技术研发不断取得突破和显著成效, 国家节能减排目标得以加快实现, 国务院新闻办公室发布的《中国应对气候变化的政策与行动》白皮书显示, 2005以来中国累计节能量占全球50%以上, 2020年碳排放强度较2005年下降了48.4%. 2020年9月22日, 习近平主席在第七十五届联合国大会一般性辩论上发表重要讲话, 宣布我国"二氧化碳排放力争于2030年前达到峰值, 努力争取2060年前实现碳中和", 自此"双碳"战略目标成为我国社会主义现代化建设中重要的指导方向之一. 未来40年, 我国经济和产业结构都将迎来重要的调整和改变, 为新兴的绿色、低碳产业的发展带来了新的机遇, 也为建立健全绿色金融体系、推动绿色金融投资、推出创新绿色金融工具等营造友好宽松的环境氛围. 多数研究机构预计, 中国实现"双碳"战略目标所需的投资规模在100万亿元以上, 绿色金融成为了当今金融领域热门的风口之一.
央行数据显示, 2020年末中国绿色贷款余额约12万亿元, 存量规模居世界第一, 但在社会融资规模存量中的比例不到5%. 此外, 当前我国绿色债券体量在2万亿元以下, 占债券比重仅为2%, 绿色投资基金则仅有2000亿元. 这些数据侧面说明了我国绿色金融市场具备广阔的发展前景. 近年来, ESG1投资规模快速发展, 截至2020年末全球ESG资产规模已达35万亿美元, 占整体资产管理规模的三分之一, 较2018年末增长15%. ESG评估信息也逐渐对投资效益产生重要影响(Amel-Zadeh et al. (2018), Pedersen et al. (2021)). 中国金融期货交易所党委书记、董事长何庆文表示"后续我们将适时选取符合中国市场需要、市场特征、有一定市场基础的产品, 参与推出ESG指数期货和绿色债券指数期货, 助力我国的绿色金融发展" (李雨琪(2021)).
1Environmental, Social and Governance, 代表环境、社会和治理, 是一种新的价值理念和评价工具.
完善和发展绿色金融体系是实现碳达峰与碳中和目标战略下的重要一环. 在"双碳"目标战略的指导下, 随着绿色金融工具的推出与支持, 绿色产业的发展具有广阔的前景, 但由于环保产业前期投入周期较长, 在实现经济效益的同时也必须兼顾社会效益, 因此会导致绿色产业的发展存在一定的不确定性. 由此, 看好或持有环保行业相关股票或指数基金的投资者将期望获得额外的风险补偿, 这种风险补偿则可以被视为绿色激励. 研究中国证券市场中绿色激励的存在性和显著性有利于进一步发现绿色风险补偿机制以及把握政策对市场的引导效应. 同时, 在股票市场中对绿色行业相关指数或股价趋势的准确预测有利于政府制定行业政策刺激绿色产业发展, 也有利于投资者采取恰当的交易策略获得投资收益等. 本文将通过探究绿色激励指标的构建方式以用于日度指数预测建模, 为跟踪和预测行业指数趋势提供新的参考思路并做出一定贡献. 下面将简要回顾现有文献中关于绿色激励和股指股价预测的研究成果.
1.1 关于绿色激励的研究
在全球产业链对环保政策的持续关注和不断加码绿色投资的背景下, 投资者的行为决策将更倾向于纳入绿色因素的考量, 从而对市场估值产生一定影响(Gimeno et al. (2022)), 因此研究绿色激励有助于对绿色市场收益率的经济解释, 并为绿色板块投资者提供有效信息. 绿色激励是绿色企业承担绿色特有风险的同时, 所获得的风险补偿. 关于中国股票市场的绿色激励现象, 已有研究者做了相关研究. 韩立岩等(2017)在Fama-French三因子模型(Fama et al. (1993))的基础上引入绿色因子构建了绿色激励四因素模型, 更好地解释了绿色概念股在2005–2014年间的超额收益率. 刘勇等(2020)以满足可持续发展标准的绿色企业为样本, 在Fama-French五因子模型(Fama et al. (2015))框架下构建六因子模型, 发现2009–2015年间在可持续发展观下, 中国股票市场存在显著且稳健的绿色激励. 韩国文等(2021)在投资组合方法和因子模型方法两个维度下, 从碳排放的视角发现中国股票市场在2012–2014年间存在显著的绿色激励, 而在2013–2017年存在显著的碳风险溢价. 申学峰(2019)指出绿色股相较非绿色股盈利能力更强, 财务风险更高, 从而产生了绿色激励现象.
1.2 关于股指股价预测的研究
得益于数字经济的快速发展, 丰富而复杂的数据结构、多样而严谨的科学理论和与时俱进的技术设备等为统计学、预测科学等领域的不断进步带来了深刻挑战与巨大机遇(洪永淼等(2021)). 股指股价的预测是金融市场经典而又重要的问题, 合理准确的预测能为投资者带来更好的收益, 因此也吸引了许多研究者参与到股指股价预测的相关研究中, 至今已发展出大量的预测技术. 最常用的两类方法为统计学方法和机器学习方法. 统计学方法中的ARIMA模型(Adebiyi et al. (2014), Ariyo et al. (2014), Bhardwaj et al. (2019)), GARCH模型(Herwartz (2017), Wang et al. (2020)), 以及机器学习方法中的支持向量机(SVM) (Bao et al. (2004), Hegazy et al. (2014), Kim (2003)), XGBoost算法(王燕等(2019), Basak et al. (2019)), 人工神经网络(Du (2018), Guresen et al. (2011)), 长短期记忆网络(马超群等(2021), Fischer et al. (2018), Selvin et al. (2017))等都被广泛应用于股指股价预测. 由于传统的统计学方法通常假定数据是由线性过程生成的, 有着较为精简的模型架构, 而机器学习方法通常会对原始数据做一些非线性的变换, 模型结构相对更加复杂(Januschowski et al. (2020)), 因此机器学习方法在预测股指股价这类呈现高度非线性性, 非平稳性以及异方差性的数据上具有更大的潜力. Adebiyi et al. (2014)使用戴尔(Dell)公司1988–2011年的股票数据比较了ARIMA模型和人工神经网络(ANN)模型的预测效果, 发现二者都有较高的预测精度, 但人工神经网络模型在多数情况下要优于ARIMA模型. Du (2018)分别用ARIMA模型和反向传播神经网络(BPNN) 模型预测上证指数, 另外以ARIMA模型预测的残差序列训练反向传播神经网络, 然后将两者的预测结果相加作为最终预测. 实证结果显示集成方法的预测效果要优于反向传播神经网络, 而反向传播神经网络要优于ARIMA模型. 孙宏鑫等(2021)利用混合神经网络模型对沪深300股指期货进行价格预测和趋势预测, 并据此设计投资策略. 该研究对比了LSTM和CNN的单模型预测结果, 论证了混合模型的优越性和趋势预测的可行性.
一般而言, 在股指股票预测模型的建模中除了直接利用原始时间序列及其滞后阶进行预测以外, 大多数预测方法还引入了其他的解释变量如盘面数据、技术指标、文本或图像数据等. 但由于目前在预测绿色股指或股价时将绿色激励指标考虑进来的相关研究较少, 这为我们探究和构建绿色激励指标并将其应用于绿色股指预测提供了研究动机.
从上述文献调研可知, 一方面绿色激励指标的构建和显著性分析等研究表明了中国股票市场中存在绿色激励, 另一方面关于绿色激励的进一步应用, 例如引入绿色激励指标进行绿色股指股票的预测和高频交易的决策等, 存在一定的研究空白. 从时间频度的及时性和指标构造的便利性等角度考虑, 由于传统的绿色激励因子以月度频率为主, 而且对市场中所有绿色概念股票和非绿色概念股票相关数据均需要进行一定地提取和处理, 对于更高频的预测(如日度预测)和投资组合决策(如绿色股票的投资组合)缺乏一定的效用. 本文提出了一种更便捷高效的构造方式, 既不失绿色激励的核心内涵, 同时能够有效提高后期的预测效果.
基于以上讨论并结合本研究内容, 本文创新点主要体现在以下三个方面:
1) 构建了一种全新的绿色激励指标.不同于现有相关研究思路, 本文以中国股票市场中证环保指数为切入点, 通过经典的资本资产定价模型及行业
2) 提出了一种全面的混合分析方法并对相关指标的性质特点进行探究. 在指标构建完成后和将其应用于实证预测研究前, 为了进一步理解GI指标的性质特点, 以及与预测目标(即中证环保指数)之间的关联性、趋势性和解释性, 本文提出了一种新的混合分析方法, 其中包括GI指标关于中证环保指数的因果检验分析、趋势分析和简单回归分析等, 能够全面地反映所建指标的优势与特点.
3) 应用绿色激励指标于绿色指数预测模型, 对该指标的预测价值进行了实证研究与讨论. 面对高度非线性和波动性的复杂数据结构, 本文利用与绿色指数相关的特征变量以及GI指标建立基于机器学习方法的指数预测模型, 并通过控制变量法进行实证分析. 整体而言, 实验结果能够从一定程度上有效支持GI指标的预测价值与参考意义.
全文结构安排如下: 第二部分介绍绿色激励指标构建方法以及相关混合分析结果, 包括对于指标的动态因果检验、相关性分析、趋势分析和简单回归分析等; 第三部分为实证研究, 将基于绿色激励指标以及其他解释变量对中证环保指数收盘价进行日度预测, 预测模型以机器学习模型为主, 同时讨论实证结果并对比简单线性模型的优劣性; 第四部分是对全文研究内容的总结与展望.
2 绿色激励指标构建与分析
本部分将具体介绍绿色激励指标的构建方法, 同时对照中国股票市场中环保行业指数, 采用混合分析方法, 对绿色激励指标进行相关动态因果检验、KL信息量与时差相关系数等趋势分析以及回归系数显著性检验等, 从而探究绿色激励指标与环保行业指数之间的关联性, 为后续指数预测工作提供有效参考.
2.1 绿色激励指标的构建
对于中国证券市场中的绿色激励, 现有研究主要是通过在控制市值规模和账面市值比后, 以绿色概念股票收益率与非绿色概念股票收益率的差值所表达, 而后运用Fama-French模型来刻画绿色效应对绿色股票超额收益率的统计显著性(韩立岩等(2017), 许瀚元(2020)). 另一方面, 本文研究和构建绿色激励指标以经典的资本资产定价模型(CAPM)为基础, 计算环保行业板块的
2本文中关于"中证环保指数"的分析或预测均指代其收盘价数据.
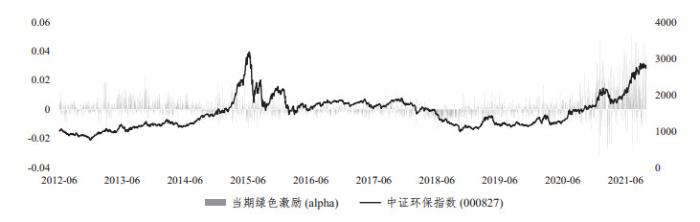
图1
从公式(2)和图 2可以看出, 绿色激励指标
图2
图3
现有相关研究在对GI指标进行构建时, 首先对不同股票依据市值规模大小和账面市值比大小进行了相应划分, 在控制相应市值和账面市值比后计算绿色概念股票与非绿色概念股票之间收益率的差值. 这种方法能够精细和全面地发现和刻画绿色激励形成机制. 然而值得一提的是, 基于以上方法对于GI的刻画在时间频度上主要以月度为主, 同时由于纳入模型的部分影响因子只有在企业公布财报后方能更新, 因此所含信息具有一定的滞后性, 对日度频率时间序列(如日度指数序列、价格序列等)预测的建模上优势亦有所欠缺. 另一方面, 本文从指标构造的时效性和便捷性出发提取整个环保行业指数所蕴含的绿色激励, 虽然构造方式不同, 但是从另一个角度也能反映绿色激励的内涵, 即绿色行业的超额风险补偿. 本方法一定程度上节省了传统方法所需的计算时间, 而通过公式(1)和公式(2)构建的GI指标能够在日度频率上获取, 有利于进一步构建指数预测模型, 为后续预测和决策奠定基础.
在GI指标构建之后, 为了加深GI对于绿色指数的关联性、趋势性和解释性等性质的理解, 通常单方面的因果分析或趋势判断具有一定的局限性, 因此我们提出并采用一种新的混合分析方法, 旨在全面地探讨与发现所建指标与预测目标之间的相关关系. 在混合分析方法中, 因果分析、趋势分析(即先行/一致/滞后等关系分析)、简单回归分析等均纳入了考量体系. 因果分析中采用动态因果检验方法, 从统计和计量经济学的角度探究GI对于绿色指数的信息溢出效应. 趋势分析中利用6种不同的评估准则, 从指标形态、相关关系和预测能力评分等方面考察GI指标对于绿色指数的趋势性与相关性. 最后通过简单回归分析中系数显著性特征以及回归方法的预测表现初步评价GI指标的优劣性. 下文将具体介绍本研究中运用的混合分析方法.
2.2 绿色激励指标的动态因果检验
因果因素是衡量预测变量优劣的重要标准, 在大数据时代背景下, 机器学习算法有助于识别相关因果变量并将其用于预测(萧政(2021)). 为研究绿色激励指标的因果因素, 本节以基于DCC-GARCH模型(Engle (2002))的动态因果检验方法, 考察本文所构建的绿色激励指标GI对中证环保指数是否具有信息溢出效应. DCC-GARCH模型常应用于研究各市场之间(Lu et al. (2017))的波动率关系或联动关系, 而应用该模型前要求输入的序列具有平稳性. 因此在实际模型输入前, 我们对中证环保指数和
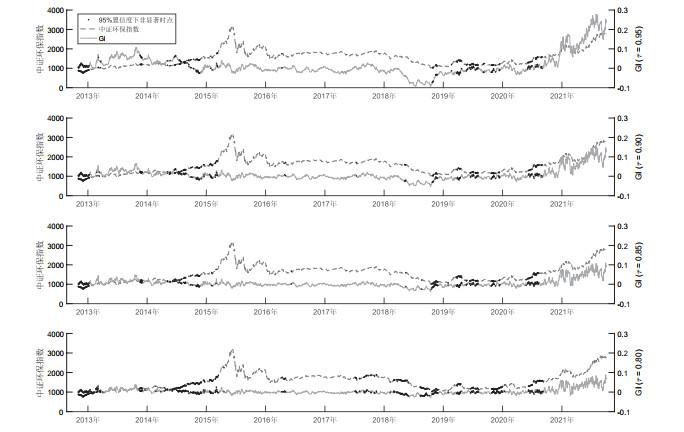
图 4对绿色激励指标的动态因果检验结果进行了相应可视化, 其中标记为黑色的点说明在对应时间节点上以95%的置信水平无法拒绝原假设, 其余时间点上表明GI指标对中证环保指数具有信息溢出. 从图中可见, 2012年11月至2021年9月期间, 在不同激励因子的设定下, GI指标在大部分时间内对中证环保指数均具备一定的信息溢出效应, 而且随着激励因子
图4
2.3 绿色激励指标的趋势分析
本文从构造绿色激励指标出发, 其落脚点旨在服务于绿色环保市场相关指数的预测建模, 也为未来进一步预测绿色股票价格和相关证券的投资组合决策提供一定的信息或解释变量的支持. 在被解释变量选为中证环保指数后, 作为解释变量的绿色激励指标GI的趋势分析既有利于从总体上把握此二者之间的相关关系和先行滞后关系, 也为预测建模中解释变量滞后阶的选取提供理论支撑.
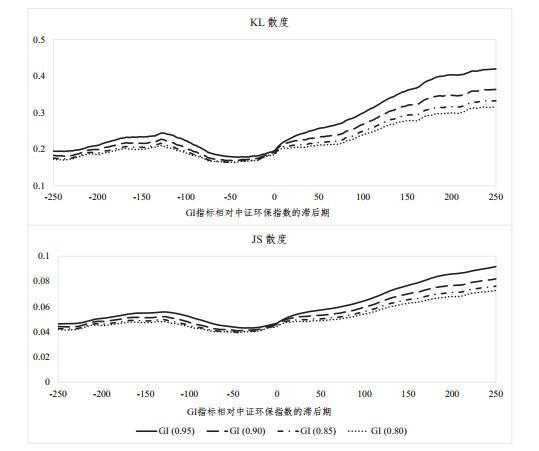
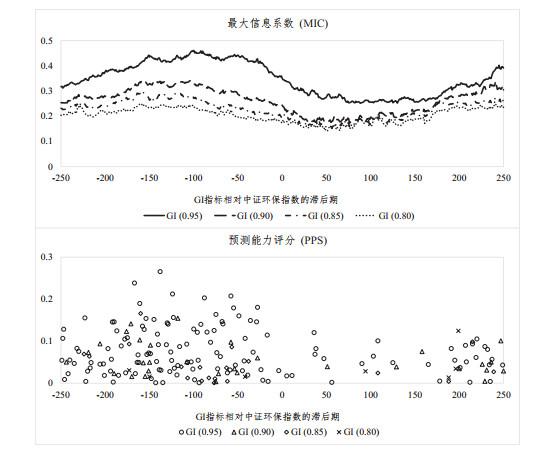
本节将借助6种检验指标之间趋势关系或相关关系的方法入手, 对GI进行趋势分析, 其分别为: 皮尔森相关系数(Pearson)、斯皮尔曼相关系数(Spearman)、Kullback-Leibler散度(KL散度)、Jensen-Shannon散度(JS散度)、最大信息系数(maximal information coefficient, MIC)和预测能力评分(predictive power score, PPS). 以下将简要介绍上述各方法的计算规则和意义内涵:
Pearson相关系数和Spearman相关系数. Pearson常用于度量两个连续变量之间的线性关系, 而Spearman则强调度量两个连续变量之间的单调关系. 设
当
KL散度和JS散度. KL散度又称为信息散度或相对熵, 它能够度量两个概率分布
KL散度具有非负性, 而JS散度取值在0到1之间, 但无论是KL散度还是JS散度, 其取值越小表明两个分布越接近.
最大信息系数MIC. MIC的概念最初发表于Science期刊(Reshef et al. (2011)), 常用于衡量两个变量
其中
预测能力评分PPS. PPS算法的提出一是为了解决部分相关性度量方法无法检测到非线性关系的问题(例如Pearson、Spearman等), 二是引入相关性的非对称性质, 即
本文在研究解释变量绿色激励指标GI与被解释变量中证环保指数的相关关系时, 不但考察了这两个变量同期的关系, 而且计算了GI的先行或滞后值同中证环保指数的相关性和趋势性. 具体而言, 本研究中使用的总数据样本为2012年11月1日至2021年9月30日的日度数据, 共计2170个交易日, 包括GI指标和中证环保指数. 按照
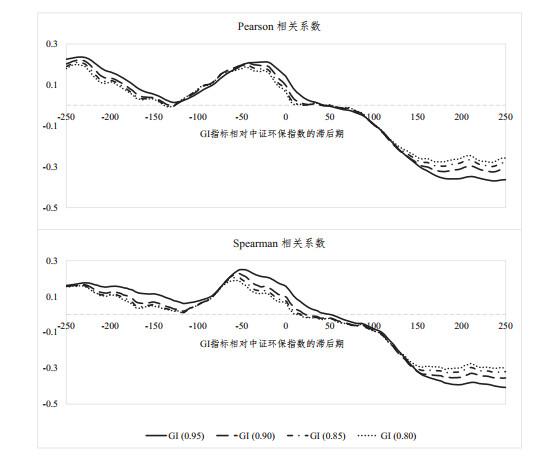
图 5
图5
图6
图7
2.4 绿色激励指标的简单回归分析
众所周知, 股指或股票价格数据具有高复杂性和高波动性等特点, 而解释变量如盘面数据、技术指标、文本情感数据等与指数或价格之间的相关关系往往是非线性的, 因此以传统计量方法进行建模通常无法达到理想的预测效果. 本节目的主要研究绿色激励指标若作为回归因子, 其回归系数是否对于预测中证环保指数收盘价具有一定的显著性. 我们将中证环保指数收盘价(
在绿色激励指标滞后阶的选择上, 我们根据相关系数的最大值、散度的最小值和MIC的最大值选择相应的滞后阶数, 并同时考虑当期GI指标(注意到根据公式(2),
表 1展示了在不同激励因子下4组多元线性回归结果. 首先, 绿色激励指标的当期或滞后期对环保指数收盘价的回归具有一定的系数显著性; 其次, 对比加入GI指标和不考虑GI指标下的线性回归预测结果, 从均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和方向准确度(Dstat)来度量预测表现, 可见加入GI指标有助于提升简单预测模型的预测精度和方向准确度; 最后, 虽然并非我们选取的所有GI滞后阶都被纳入线性回归模型中, 但是这并不能说明GI指标的滞后阶对于预测模型是失效的. 由于指数的高度非线性特征, 仅用线性模型刻画和预测既片面也不准确. 事实上, 我们将在第4部分进一步利用机器学习模型进行指数预测, 除了考虑指数自身滞后和GI指标外, 加入了更多的盘面数据和技术指标等, 以学习和获取特征中更多的知识信息. 在下一部分中我们也将指出线性模型在预测指数所表现出的缺点, 包括呈现明显的趋势跟随特性以及无法良好地捕获波动性等, 一方面说明智能方法预测的必要性, 另一方面也希望继续探究GI指标对于机器学习的预测是否同样有效.
表1 多元线性回归结果
| 组别 | 对照类型 | 解释变量(系数) | RMSE | MAE | MAPE(%) | Dstat(%) | |
| 第一组 | 无GI变量 | (0.99 | 38.28 | 27.95 | 1.52 | 45.05 | |
| 含GI变量 | (0.99 | 38.31 | 27.86 | 1.51 | 55.42 | ||
| ( | (86.12 | ||||||
| ( | |||||||
| 第二组 | 无GI变量 | (0.99 | 38.41 | 28.00 | 1.51 | 52.59 | |
| (6.12 | |||||||
| 含GI变量 | (0.99 | 38.12 | 27.71 | 1.50 | 53.54 | ||
| ( | (99.84 | ||||||
| 第三组 | 无GI变量 | (0.99 | 38.40 | 28.00 | 1.51 | 51.65 | |
| (6.23 | |||||||
| 含GI变量 | (0.99 | 38.15 | 27.74 | 1.50 | 55.19 | ||
| ( | (151.87 | ||||||
| 第四组 | 无GI变量 | (0.99 | 38.40 | 28.00 | 1.51 | 51.65 | |
| (6.23 | |||||||
| 含GI变量 | (0.99 | 38.29 | 27.88 | 1.51 | 50.00 | ||
| ( | (181.18 | ||||||
注: (1)
3 实证研究与讨论
虽然传统计量方法具有更加科学合理的模型解释性, 然而机器学习方法相较于计量模型在学习和预测高维、高波动的复杂数据时优势更为突出. 本部分将主要利用三种热门的机器学习方法(SVR, LightGBM, XGBoost)对中证环保指数收盘价进行预测. 与2.4节中多元线性回归不同的是, 在解释变量的选择上除了一阶滞后的收盘价和GI指标外, 更多的盘面数据、技术指标等也将作为特征输入预测模型. 该部分旨在探究GI指标对于机器学习方法是否仍然具备一定的预测解释力, 即是否能够提升模型预测表现. 其次我们从预测结果中发现, 从指数预测评价指标而言, 简单线性模型略优于机器学习模型, 然而从波动性刻画而言, 机器学习方法更胜一筹, 因此本文也将对这种差异性进行探讨.
3.1 数据准备
在特征变量的选择上, 对于每一组
在预测方法上, 对于每一组
3.2 模型介绍
我们将使用多种方法对股票指数进行预测, 本节将简要介绍我们所用的模型与算法, 分别为支持向量机(support vector machine, SVM) (Cortes et al. (1995))和梯度提升决策树(gradient boost decision tree, GBDT) (Friedman (2001)).
支持向量机. 支持向量机是针对二分类问题而提出的. 对于线性可分数据, 支持向量机会寻找一个超平面将两类数据分离, 并使得分离间隔最大; 对于线性不可分的数据, 则可用核技巧将原始数据映射到新空间, 再在新空间中使用线性方法得到模型. 但是支持向量机只适用于二分类问题, 故本文使用它的一个应用分支——支持向量回归(support vector regression). 支持向量回归是一个回归模型, 其目的不再是寻找超平面尽可能分离两类数据, 而是使得数据尽量拟合到超平面上. 核技巧在支持向量回归中也同样适用.
梯度提升决策树. 梯度提升决策树是基于Boosting的一种集成学习方法, 由若干决策树串联构成——训练时, 每棵树学习在它之前的所有树的预测结果之和与真实值的残差. 梯度提升决策树具有很强的学习能力, 但如果不经过额外的正则化处理, 容易发生过拟合. 此外, 由于各决策树之间存在依赖关系, 训练过程难以并行, 计算复杂度较高. 因此本文将使用梯度提升决策树的两个改进方法XGBoost (Chen et al. (2016))和LightGBM (Ke et al. (2017)). XGBoost在梯度提升决策树的基础上做了大量的优化, 是梯度提升决策树算法的工程实现, 使用时更加高效灵活. 它在目标函数中显式地加入正则项防止过拟合, 并将损失函数进行二阶泰勒展开, 提高了计算的精确度. LightGBM也是梯度提升决策树框架下的一种优化改进. 它采用直方图算法将连续特征进行分段化处理, 从而降低了时间复杂度和空间复杂度. 同时, LightGBM采用leaf-wise策略生长树, 相较于多数决策树生长树所用的level-wise策略可以减少更多的损失. 并且LightGBM也提供了并行学习优化算法. 值得一提的是, XGBoost和LightGBM的性能同样也依赖于超参数的设定, 如何调参是机器学习领域一个重要问题, 但是本文对此并不展开研究, 仅凭经验设定模型的超参数, 而未进行优化.
3.3 预测结果与讨论
表 2展示以均方根误差(RMSE), 绝对平均误差(MAE), 绝对平均百分比误差(MAPE)和方向统计量(Dstat)为评价指标, 分别使用SVR, XGBoost和LightGBM在测试集上预测效果.
表2 机器学习模型结果
| 模型 | RMSE | MAE | MAPE(%) | Dstat(%) |
| SVR | 39.39 | 28.53 | 1.55 | 51.42 |
| SVR (0.95) | 39.42 | 28.32 | 1.53 | 53.54 |
| SVR (0.90) | 39.66 | 28.51 | 1.54 | 51.42 |
| SVR (0.85) | 39.63 | 28.47 | 1.54 | 51.42 |
| SVR (0.80) | 39.34 | 28.41 | 1.54 | 53.30 |
| XGBoost | 47.39 | 35.34 | 1.90 | 50.71 |
| XGBoost (0.95) | 45.29 | 33.40 | 1.80 | 51.18 |
| XGBoost (0.90) | 47.88 | 34.97 | 1.88 | 52.59 |
| XGBoost (0.85) | 46.99 | 34.86 | 1.88 | 52.12 |
| XGBoost (0.80) | 54.74 | 39.05 | 2.08 | 51.65 |
| LightGBM | 56.26 | 40.42 | 2.15 | 49.76 |
| LightGBM (0.95) | 53.52 | 38.51 | 2.05 | 52.59 |
| LightGBM (0.90) | 56.03 | 39.58 | 2.10 | 51.89 |
| LightGBM (0.85) | 55.67 | 39.92 | 2.13 | 51.65 |
| LightGBM (0.80) | 63.32 | 43.87 | 2.31 | 50.24 |
注: (1)模型名称后括号中的数字表示此模型在预测时使用该激励因子
从表 2中我们发现, 使用XGBoost和LightGBM时, 加入绿色激励指标可以改善预测结果, 不同的激励因子对预测精度的改进程度也有所不同, 在模型中加入较大激励因子
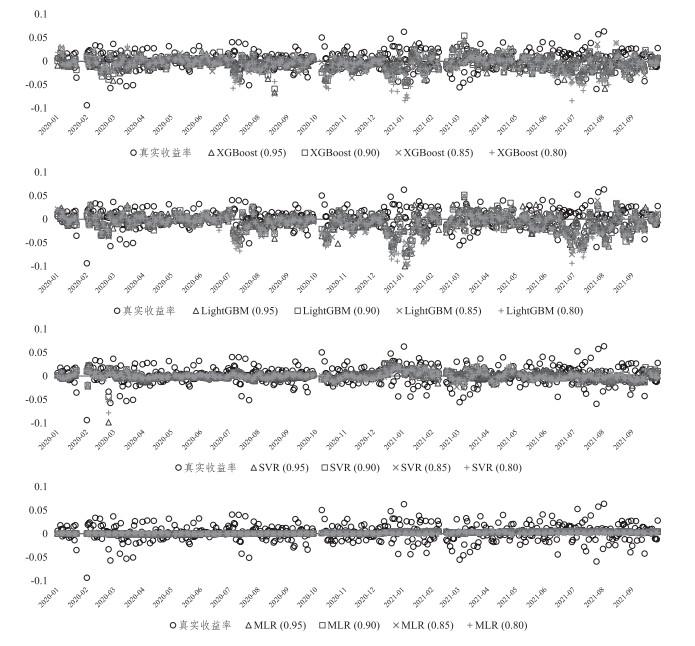
1) 从模型预测机理来看, 线性回归模型倾向于预测趋势, 而机器学习模型倾向于预测值(Adebiyi et al. (2014)). 这种特性导致线性回归模型具有比较强的趋势跟随性, 即模型对第
图8
2) 正如前文提到的, 机器学习方法的性能往往依赖于超参数的设定, 考虑到我们是采用滚动窗口的方式预测的, 训练数据的不同导致每一期的预测时所用的模型也不同, 如果对每一期的模型进行调参, 则需要大量的时间成本. 若不计时间成本对超参数进行优化, 机器学习方法在预测精度上有进一步提高的潜力.
另一方面, 本文所构建的GI指标对比传统绿色激励指标具有时效性、便捷性和较强的预测解释性等优点, 更适用于作为预测模型的解释变量. 现有相关文献主要通过Fama-French因子模型及其变体形式, 对传统绿色激励指标进行回归分析, 对于认识我国证券市场中绿色激励效应的存在性与显著性具有重要意义. 然而, 由于传统的绿色激励指标具有较高的构造复杂度以及较低的时间频度(以月度为主)等局限性, 在指标构造过程中尤其需要获取财报数据, 例如账面市值比、息税前利润、投入产出比率等, 进而导致传统指标具有一定的滞后性(财报数据通常滞后数日甚至数月才发布)和弱解释性(例如5、6月的指标构造只能采用一季报的数据, 不能反映当前水平). 从预测的角度而言, 传统GI指标的时滞性和低频特征等缺点为高频预测来带一定的困难和挑战, 这也是本文提出一种新的GI指标构建方法的主要动机来源.
3.4 不同激励因子下GI预测能力的适应性研究
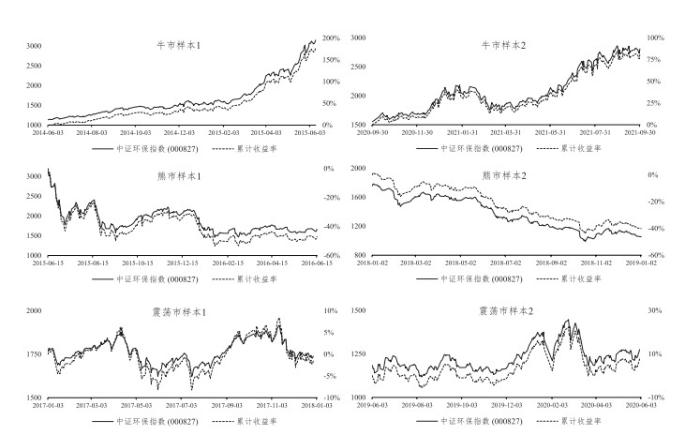
本节旨在研究与讨论在不同激励因子设定下构建的GI指标适用环境的差异性. 具体而言, 不同激励因子
如图 9所示, 我们对绿色指数进行了样本采样, 分别包括两条牛市样本序列(2014年6月3日– 2015年6月12日, 2020年9月30日– 2021年9月30日), 均呈现明显上升趋势, 其区间累计收益率分别为176.75%和80.83%; 两条熊市样本序列(2015年6月15日– 2016年6月15日, 2018年1月2日– 2019年1月2日), 均呈现显著下跌态势, 其区间累计收益率分别为
图9
与3.1和3.2节类似, 我们将每一段时期的样本进一步划分为训练集(80%)和测试集(20%), 采用滚动预测的方式, 对各个模型进行了评估, 结果如表 3所示. 从表中结果可知, 在三种市场阶段的六条序列样本上, 对比无GI变量加入的预测模型, 在预测模型的变量集合中考虑GI指标将有助于提升模型的预测表现, 该结果与3.3节中相关结论具有一致性. 从不同的市场阶段来看, 对于牛市和熊市阶段, 激励因子较大的GI指标的预测解释性优于较小
表3
不同
| 牛市阶段 | ||||||||||
| 样本1 | 样本2 | |||||||||
| 模型 | RMSE | MAE | MAPE | Dstat | RMSE | MAE | MAPE | Dstat | ||
| SVR | 61.01 | 45.88 | 1.81 | 70.00 | 59.18 | 44.95 | 1.67 | 56.25 | ||
| XGB | 72.26 | 60.06 | 2.32 | 56.00 | 75.22 | 56.39 | 2.08 | 65.50 | ||
| LGB | 73.24 | 55.49 | 2.17 | 50.00 | 81.92 | 68.57 | 2.53 | 52.08 | ||
| SVR | 61.63 | 46.15 | 1.82 | 70.00 | 59.12 | 44.80 | 1.66 | 56.25 | ||
| XGB | 70.18 | 58.57 | 2.26 | 52.00 | 81.11 | 63.05 | 2.33 | 56.25 | ||
| LGB | 70.33 | 54.92 | 2.10 | 62.00 | 87.88 | 70.52 | 2.61 | 58.33 | ||
| SVR | 61.58 | 46.14 | 1.82 | 70.00 | 59.40 | 44.92 | 1.66 | 56.25 | ||
| XGB | 73.96 | 61.59 | 2.38 | 54.00 | 81.17 | 63.85 | 2.35 | 47.92 | ||
| LGB | 70.20 | 59.71 | 2.31 | 50.00 | 95.07 | 74.26 | 2.75 | 54.17 | ||
| SVR | 61.62 | 46.30 | 1.83 | 70.00 | 59.44 | 45.04 | 1.67 | 56.25 | ||
| XGB | 70.55 | 59.30 | 2.29 | 54.00 | 81.26 | 64.42 | 2.37 | 54.17 | ||
| LGB | 74.59 | 61.90 | 2.39 | 48.00 | 97.51 | 74.78 | 2.76 | 58.33 | ||
| 无GI变量 | SVR | 61.66 | 46.26 | 1.82 | 70.00 | 60.37 | 46.38 | 1.72 | 60.42 | |
| XGB | 80.08 | 64.29 | 2.45 | 56.00 | 76.80 | 57.97 | 2.13 | 58.33 | ||
| LGB | 80.41 | 64.50 | 2.45 | 60.00 | 86.88 | 72.66 | 2.68 | 56.25 | ||
| 熊市阶段 | ||||||||||
| 样本1 | 样本2 | |||||||||
| 模型 | RMSE | MAE | MAPE | Dstat | RMSE | MAE | MAPE | Dstat | ||
| SVR | 28.26 | 19.41 | 1.17 | 52.08 | 18.12 | 14.00 | 1.28 | 52.08 | ||
| XGB | 38.81 | 29.30 | 1.78 | 66.67 | 24.11 | 19.27 | 1.75 | 54.17 | ||
| LGB | 45.30 | 34.73 | 2.08 | 58.33 | 33.80 | 25.42 | 2.30 | 45.83 | ||
| SVR | 28.33 | 19.39 | 1.17 | 52.08 | 18.01 | 13.75 | 1.25 | 60.42 | ||
| XGB | 42.46 | 32.40 | 1.96 | 54.17 | 30.63 | 22.03 | 2.00 | 45.83 | ||
| LGB | 48.90 | 38.78 | 2.32 | 52.08 | 38.27 | 28.61 | 2.61 | 60.42 | ||
| SVR | 28.34 | 19.40 | 1.17 | 52.08 | 17.85 | 13.65 | 1.24 | 60.42 | ||
| XGB | 40.78 | 31.65 | 1.92 | 58.83 | 26.54 | 20.43 | 1.85 | 52.08 | ||
| LGB | 46.71 | 38.40 | 2.32 | 50.00 | 34.97 | 27.89 | 2.55 | 56.25 | ||
| SVR | 28.37 | 19.43 | 1.17 | 52.08 | 16.76 | 12.87 | 1.17 | 50.00 | ||
| XGB | 46.89 | 35.93 | 2.17 | 60.41 | 30.47 | 22.68 | 2.06 | 47.92 | ||
| LGB | 46.89 | 38.29 | 2.31 | 58.33 | 48.18 | 35.68 | 3.27 | 56.25 | ||
| 无GI变量 | SVR | 28.38 | 19.46 | 1.18 | 52.08 | 16.73 | 13.11 | 1.19 | 52.08 | |
| XGB | 48.75 | 36.32 | 2.18 | 60.42 | 27.91 | 21.60 | 1.97 | 35.42 | ||
| LGB | 50.37 | 41.44 | 2.50 | 56.25 | 45.34 | 38.53 | 3.50 | 52.08 | ||
| 震荡市阶段 | ||||||||||
| 样本1 | 样本2 | |||||||||
| 模型 | RMSE | MAE | MAPE | Dstat | RMSE | MAE | MAPE | Dstat | ||
| SVR | 20.49 | 15.98 | 0.89 | 50.00 | 19.92 | 14.93 | 1.22 | 45.83 | ||
| XGB | 23.01 | 18.50 | 1.03 | 50.00 | 23.51 | 19.10 | 1.55 | 52.08 | ||
| LGB | 24.63 | 17.99 | 1.00 | 54.17 | 26.57 | 20.64 | 1.67 | 60.42 | ||
| SVR | 20.47 | 15.93 | 0.89 | 50.00 | 19.98 | 14.93 | 1.22 | 50.00 | ||
| XGB | 22.40 | 17.98 | 1.00 | 52.08 | 23.15 | 18.28 | 1.49 | 50.00 | ||
| LGB | 22.97 | 17.39 | 0.97 | 58.33 | 25.76 | 20.38 | 1.66 | 58.33 | ||
| SVR | 20.48 | 15.95 | 0.89 | 47.92 | 19.96 | 14.92 | 1.22 | 50.00 | ||
| XGB | 22.45 | 17.22 | 0.96 | 58.33 | 23.66 | 17.82 | 1.45 | 50.00 | ||
| LGB | 24.40 | 19.18 | 1.07 | 60.42 | 27.03 | 20.43 | 1.65 | 56.25 | ||
| SVR | 20.48 | 15.96 | 0.89 | 47.92 | 19.96 | 14.91 | 1.21 | 50.00 | ||
| XGB | 22.11 | 18.05 | 1.00 | 47.92 | 23.14 | 18.35 | 1.49 | 52.08 | ||
| LGB | 22.74 | 17.13 | 0.95 | 64.58 | 25.76 | 20.63 | 1.67 | 64.58 | ||
| 无GI变量 | SVR | 20.50 | 15.96 | 0.89 | 47.92 | 19.98 | 14.93 | 1.22 | 50.00 | |
| XGB | 24.86 | 21.47 | 1.19 | 45.83 | 27.29 | 20.81 | 1.69 | 52.08 | ||
| LGB | 28.96 | 23.07 | 1.28 | 47.91 | 30.76 | 23.83 | 1.93 | 52.08 | ||
注: (1) SVR均采用线性核, XGB和LGB分别指3.2节中的XGBoost和LightGBM模型. (2) MAPE和Dstat的结果均为百分数(%).
本实验论证了在不同激励因子
此外, 在
4 总结与展望
从现有文献中可知, 中国证券市场上的绿色概念股存在显著的超额收益, 其源于绿色股承担特有风险时带来的风险补偿, 即绿色激励. 不同于传统的绿色激励指标构造方法, 为了探究绿色激励并将其应用于日度绿色股指预测, 本文从指标构造的便捷和实用性出发, 参考经典的资本资产定价模型, 构建了四种不同激励因子下的绿色激励指标. 同时, 为了进一步理解所建指标的性质特征以及其与预测目标之间的关系, 我们提出了一种新的混合分析方法, 包括因果分析、趋势分析以及简单回归分析等. 其中, 本研究使用2012年11月到2021年9月的中证环保指数检验绿色激励指标与环保指数之间的动态因果关系, 结果显示绿色激励指标对于中证环保指数在大部分时间中都存在显著的信息溢出. 为了构建日度预测模型, 我们利用训练集信息对绿色激励指标和中证环保指数进行了相应的相关性分析和趋势分析, 既表明了GI指标关于中证环保存在一定的先行特征, 又为预测模型的解释变量GI滞后阶的判定提供一定依据. 简单的多元线性回归结果也证实了GI指标存在线性显著性, 同时能够提升回归模型的预测表现. 考虑到线性模型的预测缺陷, 本文考虑了更多的解释变量, 包括盘面数据和技术指标等, 并利用机器学习方法如XGBoost, LightGBM和SVR等对中证环保指数收盘价进行预测, 其中既考察了加入GI与否是否造成预测表现差异, 又对比了智能模型和简单线性方法的预测能力区别. 实证研究结果显示, GI指标在机器学习模型中仍然能够提供额外的信息以提升模型的预测精度, 尤其是在激励因子较高水平下构造的GI. 对比线性模型, 虽然智能方法在传统的评价准则下或许显得不及简单方法, 但是从收益率的角度来看, 由于简单线性回归存在较强的趋势跟随, 无法良好刻画和预测未来波动特征, 从侧面突出了智能方法的优势. 总而言之, 本文提出的绿色激励指标构造方法对于高频的日度绿色指数预测能够提供有效信息, 在不同激励因子下构造的GI指标具备不同市场阶段的适用性, 并在一定程度上提升预测精度.
本文的研究方法主要体现在绿色指标的构造、分析和预测应用上. 从指标构造方面而言, 得益于方法的实用性和便捷性, 该方法也适用于单只绿色股票乃至其他投资板块中激励指标的构建. 从指标分析方法而言, 该混合分析方法有助于提前对各类预测解释变量进行特征分析与特征筛选, 并检验其可解释性与可预测性. 在预测领域, 本方法能够考察和分析例如宏观经济预测模型中加入的合成指数、价格或波动率预测模型中考虑的文本情感指数等新型指标与预测目标之间的相关关系, 进而拥有广阔的应用空间. 此外, 本文所提出的绿色激励指标不仅能够应用于预测领域, 在决策领域中例如设计绿色股票的投资组合策略时也可考虑绿色激励的影响. 因此在未来研究中, 我们将于解释变量中纳入更多的信息, 例如搜索指数和文本情感数据等; 在机器学习模型构建上将持续优化模型结构并调整超参数, 以进一步提升指数预测精度; 在预测目标上, 下一步将探究绿色激励对波动率或收益率预测的有效性和可行性; 在后期决策中, 特别在基于机器学习的绿色股票的投资组合方法中, 组合权重的优化将纳入绿色激励和模型预测值等.
参考文献
企业碳排放与股票收益——绿色激励还是碳风险溢价
[J].
Corporate Carbon Emissions and Stock Returns: Green Incentive or Carbon Risk Premium?
[J].
中国证券市场的绿色激励: 一个四因素模型
[J].
Green Incentive in Chinese Securities Market: Four Factor Model
[J].
大数据, 机器学习与统计学: 挑战与机遇
[J].
Big Data, Machine Learning and Statistics: Challenges and Opportunities
[J].
中国股票市场的绿色激励: 可持续发展视角
[J].
Does Chinese Stock Market Reward for Going Green? Based on Enterprise Sustainable Development
[J].
基于H-LSTM模型的沪深300指数价格预测研究
[J].
The Prediction of Shanghai and Shenzhen 300 Index Based on H-LSTM Model
[J].
A股市场的绿色激励现象及其产生原因
[J].
The Phenomenon of Green Incentives in the A-share Market and Its Causes
[J].
基于趋势学习的混合神经网络股指期货预测研究
[J].
Research on Stock Index Futures Forecast Based on Trend Learning and Hybrid Neural Network
[J].
改进的XGBoost模型在股票预测中的应用
[J].
Application of Improved XGBoost Model in Stock Forecasting
[J].
大数据时代关于预测的几点思考
[J].
Some Thoughts on Prediction in the Presence of Big Data
[J].
Comparison of ARIMA and Artificial Neural Networks Models for Stock Price Prediction
[J].
Why and How Investors Use ESG Information: Evidence from a Global Survey
[J].
Predicting the Direction of Stock Market Prices Using Tree-based Classifiers
[J].
Prediction of Stock Market Using Machine Learning Algorithms
[J].
Support-vector Networks
[J].
Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models
[J].
Common Risk Factors in the Returns on Stocks and Bonds
[J].
A Five-factor Asset Pricing Model
[J].
Deep Learning with Long Short-term Memory Networks for Financial Market Predictions
[J].
Greedy Function Approximation: A Gradient Boosting Machine
[J].
The Role of a Green Factor in Stock Prices. When Fama French Go Green
[J].
Using Artificial Neural Network Models in Stock Market Index Prediction
[J].
A Machine Learning Model for Stock Market Prediction
[J].
Stock Return Prediction under GARCH — An Empirical Assessment
[J].
Granger Causality in Risk and Detection of Extreme Risk Spillover between Financial Markets
[J].
Criteria for Classifying Forecasting Methods
[J].
Financial Time Series Forecasting Using Support Vector Machines
[J].
Equitability, Mutual Information, and the Maximal Information Coefficient
[J].
Time-varying Coefficient Vector Autoregressions Model Based on Dynamic Correlation With an Application to Crude Oil and Stock Markets
[J].
Responsible Investing: The ESG-efficient Frontier
[J].
Detecting Novel Associations in Large Data Sets
[J].
Forecasting Stock Price Volatility: New Evidence from the GARCH-MIDAS Model
[J].