1 引言
宏观审慎的政策目标是防范系统性金融风险以维护金融稳定, 它是一个动态发展的政策框架, 着眼于管理金融的顺周期性和危机的传染性, 内容包含对银行的资本要求、杠杆率要求、流动性要求和系统性重要金融机构的特别要求等(周小川(2011)). 宏观审慎这一概念主要发展于2008年金融危机后, 与微观审慎相对应. 微观审慎关注单个金融机构在经营过程中所面临的各类风险, 以确保单个金融机构稳健运营为目标, 认为只要确保单个金融机构稳定, 就能保证整个金融体系稳定. 2008年金融危机的爆发, 微观审慎理念受到挑战, 人们认识到由羊群效应、动物精神等集体失误推动的金融顺周期性以及危机在金融体系中的传染性等原因, 将导致微观审慎性的总和不等于宏观审慎性, 健康的微观主体总和并不能保证健康的宏观整体. 于是, 很多国家和国际相关组织开始着眼于金融体系整体, 探索维护金融稳定的政策管理工具, 宏观审慎政策框架应运而生.
2009年初, 国际清算银行首先提出了宏观审慎监管的概念, 指出"大而不能倒"、顺周期性、监管不足和标准不高是导致这次金融危机的主要问题, 并将维持金融稳定, 防范系统性风险作为宏观审慎监管的主要目的. 2009年4月, 二十国集团(G20)伦敦峰会首次将宏观审慎政策框架列入公报文件. 同年9月, G20匹兹堡峰会在正式形成的会议文件中开始正式引用"宏观审慎管理"和"宏观审慎政策"的概念. 2010年11月, G20首尔峰会形成并批准了宏观审慎管理的基础性框架, 同年12月16日《巴塞尔协议Ⅲ》正式公布, 确认了G20首尔峰会通过的监管框架改革内容. 目前, 宏观审慎政策作为应对金融稳定的工具, 正在国际社会迅速获得支持. 无论是发达国家, 还是发展中国家, 均会采用宏观审慎政策工具防范系统性金融风险, 而且宏观审慎政策工具的使用频率也大幅提高(Akinci and Olmstead-Rumsey (2018), Cerutti et al. (2017)). 中国作为G20的重要成员, 也积极参与到宏观审慎政策的探索与实践中. 在2009年第三季度中国货币政策执行报告中, 首次提出"要将宏观审慎管理制度纳入宏观调控政策框架". 党的十七届五中全会明确提出要"构建逆周期的金融宏观审慎管理制度框架", 而且党的十九大报告指出要"健全货币政策和宏观审慎政策双支柱调控框架, 深化利率和汇率市场化改革, 健全金融监管体系, 守住不发生系统性金融风险的底线". 可见, 当前防范和化解系统性金融风险是国家重大战略, 而宏观审慎已成为维护金融稳定的核心政策, 在近十几年的时间里政府金融管理机构的实践和国内学者的理论研究均取得了长足的进步与发展.
正如货币政策的有效性是货币政策理论研究中的核心问题一样, 宏观审慎政策的有效性也是宏观审慎理论研究的核心问题. 对宏观审慎政策能否实现预定目标, 降低系统性风险, 维护金融稳定这一问题的回答, 有助于管理当局科学地构建宏观审慎政策框架, 合理地实施并调整宏观审慎政策, 进而实现防范系统性金融风险和维护金融稳定的目标. 已有关于宏观审慎政策有效性的研究, 普遍认为宏观审慎政策工具在调控其特定直接目标方面是有效的, 如信贷类宏观审慎政策工具可有效地降低由于信贷增加或资产价格上升引起的系统性风险, 流动类宏观审慎政策工具可有效地降低系统性流动风险, 资本类宏观审慎工具可有效地降低杠杆率升高带来的系统性风险(Lim et al. (2011), Dell' Ariccia et al. (2012), Cerutti et al. (2017), Akinci and Olmstead-Rumsey (2018)). 关于我国宏观审慎政策有效性的研究也支持类似结论, 如贷款价值比能有效影响我国的房价走势和银行信贷扩张(方意(2016), 梁琪等(2015)), 存贷比可有效影响我国的信贷增长(方意(2016)), 差别存款准备金动态调整机制能有效降低银行信贷扩张和杠杆率放大(梁琪等(2015)). 可见, 已有研究支持不同类型的风险需采用不同类型的宏观审慎政策工具进行精准应对这一结论, 同时, 也体现了宏观审慎政策具有针对性强的特点. 但也正是由于针对性强这一特点, 金融机构可通过规避监管和跨境套利等手段, 使得风险转移至监管不强的其他部门和地区, 从而可能带来更严重的后果. 因此, 从整体金融稳定和系统性金融风险的意义上探讨宏观审慎的有效性, 具有重要的理论价值和现实意义(Cerutti et al. (2017), Angelini et al. (2011)).
研究宏观审慎有效性的方式主要有两类. 一类是从理论模型的角度分析宏观审慎政策的有效性, 最常见的模型是包含金融摩擦的DSGE模型(Angelini et al. (2011), 马勇和陈雨露(2013), 王爱俭和王璟怡(2014)). 另一类是从计量经济学的实证角度分析宏观审慎政策的有效性. 接下来的部分我们将从实证研究中数据来源和宏观审慎政策目标及研究方法三方面讨论已有研究存在的不足, 并指出本文的贡献所在.
从数据来源来看, 已有文献主要在Shim (2013)构建的宏观审慎数据库及IMF在2013–2014年期间全球宏观审慎政策工具(Global Macroprudential Policy Instruments, 简称GMPI)调查数据库的基础上展开研究. Cerutti et al. (2017)基于GMPI调查数据库, 对12种宏观审慎政策工具是否正在实施进行0/1赋值, 最后通过加总这12种政策工具的取值, 构建了119个国家的宏观审慎政策指数. Akinci and Olmstead-Rumsey (2018)在Shim (2013)和GMPI这两个数据库的基础上, 综合考虑了7类宏观审慎政策工具, 先对这7类政策工具的变化分别赋值
从宏观审慎的政策目标来看, 宏观审慎的目标是防范系统性风险, 维护金融稳定. 但已有文献主要研究了宏观审慎政策对信贷增长、房价增速和杠杆率等变量的影响, 缺乏对系统性金融风险影响的研究. 如Akinci and Olmstead-Rumsey (2018), Cerutti et al. (2017), IMF (2012)分析了宏观审慎政策对信贷增长和房价增长的影响. Bruno et al. (2017)分析了宏观审慎政策对银行资本流动以及债券流动的影响. Lim et al. (2011)研究了宏观审慎政策对信贷增长、系统性流动性、杠杆率及资本流动的影响. 刘泽琴等(2022)选择了宏观杠杆率和房价增速作为金融稳定的代理变量. 这些研究表明宏观审慎政策的主要优势在于针对性强, 相比货币政策工具和财政政策工具, 政策调控效果更精确、更有效, 其政策外溢效果更小. 然而, Lim et al. (2011), Dell' Ariccia et al. (2012)指出宏观审慎政策工具针对性强的特点会使金融机构进行规避监管或跨境套利, 导致风险转移至监管不强的其他部门, 从而可能造成更严重的后果. Cerutti et al. (2017)提出需对宏观审慎政策对整体系统性风险的影响展开进一步研究. Angelini et al. (2011)也指出现代宏观经济模型中最主要的缺点之一便是缺乏系统性金融风险好的代理变量. 因此, 探讨宏观审慎政策对系统性金融风险的影响效应具有重要的理论价值和现实意义. 本文在综合比较各种系统性风险测度模型的基础上, 选择了Brownlees and Engle (2017)提出的系统性风险指数SRISK来刻画整个金融系统的系统性风险. 基于Brownlees and Engle (2017)的方法, 测度了我国2022年5月31日前上市的126个金融机构的SRISK指数, 加总构成总的SRISK指数来反映我国系统性金融风险.
从研究方法来看, 已有文献主要有两类研究方法. 一类是采用动态面板数据研究宏观审慎政策的有效性, 并针对特定国家进行案例分析. Lim et al. (2011)采用49个国家2000–2010年的数据分析了宏观审慎政策的有效性, 并对中国、哥伦比亚、东欧、西班牙、韩国和美国等国家的宏观审慎政策实施情况进行了简单的案例分析. Akinci and Olmstead-Rumsey (2018)采用57个国家
综上所述, 本文的研究目标是科学地量化评估中国宏观审慎政策对金融稳定的影响效应, 帮助推动宏观审慎监管部门科学决策, 进而有助于防范和化解系统性金融风险. 较之已有文献, 本文的边际贡献体现在以下三方面: 第一, 本文形成了我国2000年1月至2022年5月的月度宏观审慎数据库, 并在此基础上构建了宏观审慎政策指数, 一定程度上解决了对宏观审慎政策效应进行量化分析的数据难题. 第二, 本文关注宏观审慎对整体金融稳定的影响, 从系统性风险的角度评估宏观审慎政策的有效性, 更全面地分析了宏观审慎政策的有效性, 进一步深化了已有研究对宏观审慎有效性的认识. 第三, 本文采用了最新发展的Rubin因果效应框架下的现代宏观经济政策评估模型量化评估了中国宏观审慎政策对金融稳定的影响效应, 为分析特定国家各种宏观审慎政策工具的综合影响提供了新的计量方法与手段.
本文的结构安排如下: 第1部分指出了本文的研究背景、意义及贡献; 第2部分在详细梳理了我国宏观审慎政策工具及使用历史的基础上, 构建了我国宏观审慎政策指数, 并分析了我国宏观审慎政策使用情况和发展脉络; 第3部分介绍了SRISK的设计思路、定义及估计方法, 测度了我国SRISK, 并分析了我国SRISK发展过程; 第4部分介绍了Rubin因果效应框架下的现代宏观经济政策评估模型, 并实证分析了我国宏观审慎政策的政策效应; 第5部分为结论与政策建议部分, 对实证分析结果进行了总结, 并提出相应的政策建议.
2 中国宏观审慎政策工具分析及指数构建
我们首先需要建立宏观审慎指数以进行宏观审慎政策效果的量化分析. 在构建宏观审慎指数的过程中, 本部分首先确定了构建宏观审慎指数所采用的四类14种政策工具, 接着以我国相应政策文件为主, 结合Shim (2013), Cerutti et al. (2017), Akinci and Olmstead-Rumsey (2018), 刘泽琴等(2022)宏观审慎数据库中对中国宏观审慎政策工具的识别与梳理, 采用Akinci and Olmstead-Rumsey (2018)的宏观审慎指数构建方法, 建立了2000年1月–2022年5月期间我国月度宏观审慎政策指数. 最后, 分析了我国宏观审慎政策工具的使用情况及发展脉络.
2.1 我国宏观审慎政策工具及使用历史
宏观审慎政策管理工具主要借鉴微观审慎政策工具. 宏观审慎监管着眼于金融体系整体, 目的是防范系统性风险, 维护金融稳定. 微观审慎监管则关注单个金融机构经营过程中所面临的各类风险, 以确保单个金融机构稳健运营为目标. Crockett (2000)指出, 宏观审慎与微观审慎最大差别在于影响经济的方式和实现的目标不同, 与实现这些目标所使用的工具无关. 方意(2016)也指出当某一政策工具着眼于整个金融系统, 目标是限制系统性风险, 维持金融稳定时, 该政策工具便具有了宏观审慎性. 2021年12月发布的《宏观审慎政策指引》进一步明确了"宏观审慎政策会运用一些与微观审慎监管类似的工具, ……但两类工具的视角、针对的问题和采取的调控方式不同". 从这个意义上来讲, 虽然我国宏观审慎监管框架在2009年才首次提出, 但是宏观审慎工具的实施却已有较长的历史. 比如, 着眼于整体金融系统稳定、管理银行部门流动性的存贷比监管指标从1995年到2015年实施了20年, 在这20年间, 虽然75%的上限规定没有变动, 但随着经济金融状况的变化具体的测算方法调整了5次. 用于管理住房抵押贷款市场中借款者贷款比例的贷款价值比在我国自2000年以来也调整了17次. 根据我国宏观审慎监管实践, 本文聚焦于信贷类、资本类、流动类及其它类这四类政策工具来构建宏观审慎政策指数.
第一类是信贷类政策工具, 本文考虑了贷款估值比(LTV)、债务收入比(DTI)和信贷限额(CL)三种工具. 贷款估值比是贷款金额占抵押品价值的比例, 如房产抵押贷款. 我国一般规定首套房贷首付比不低于20%
第二类是资本类政策工具, 本文考虑了逆周期资本缓冲(CCyB)、动态拨备(DP)、杠杆率(LEV)、系统重要金融机构资本附加(SIFI)和跨境融资宏观审慎管理(CBF)这五种工具. 逆周期资本缓冲在《巴塞尔协议Ⅲ》中提出, 要求在经济上行时计提逆周期缓冲资本, 抑制信贷过度增长, 以备在经济下行时释放逆周期缓冲资本, 抵抗信贷过度收缩可能造成的损失. 我国在2012年6月修订的《商业银行资本管理办法(试行)》中提出逆周期资本计提要求为0
动态拨备是指商业银行在经济上行时期多计提贷款损失准备, 以覆盖经济下行期的贷款损失. 2004年2月发布的《关于股份制商业银行风险评级体系(暂行)》首次提出拨备覆盖率, 2010年11月在《关于加强当前重点风险防范工作的通知》中提出了动态拨备监管的原型, 并在2011年颁布《商业银行贷款损失准备管理办法》正式建立了动态拨备制度. 2020年5月, 《关于阶段性调整中小商业银行贷款损失准备监管要求的通知》将中小商业银行贷款拨备率阶段性下调为1.5%
杠杆率监管指标于2010年由《巴塞尔协议Ⅲ》引入, 《巴塞尔协议Ⅲ》指出杠杆率作为简单、透明且不具风险敏感性的监管工具, 一方面可以限制银行体系杠杆率的累积, 另一方面可为资本充足率提供一个资本监管要求的底线. 2011年6月我国《商业银行杠杆率管理办法》提出4%的杠杆率监管红线, 2015年2月施行的《商业银行杠杆率管理办法(修订)》主要对杠杆率计算的分母做了三项调整, 起到给银行减负的作用.
系统重要性金融机构资本附加是对系统性重要金融机构的额外资本要求, 使其更多地积累资本, 增强应对系统性金融风险的能力, 由《巴塞尔协议Ⅲ》提出. 2011年5月我国银监会发布了《中国银监会关于中国银行业实施新监管标准的指导意见》, 增加了1%的系统重要性金融机构的资本附加要求. 2012年6月修订的《商业银行资本管理办法(试行)》中规定国内系统重要性银行附加资本为风险加权资产的1%. 2018年11月颁布了《关于完善系统重要性金融机构监管的指导意见》, 为系统重要性金融机构评估和监管工作机制等指明了方向. 2021年1月《系统重要性银行评估办法》实施, 明确了我国系统重要性银行认定的基本规则. 2021年12月, 《系统重要性银行附加监管规定(试行)》实施.
跨境融资宏观审慎管理是为了防止国内银行系统受到国外经济不良情况的传染, 控制系统性风险扩大的工具. 2013年5月, 外汇局出台了《关于加强外汇资金流入管理有关问题通知》, 强化银行结售汇头寸管理, 有效地缓解了外汇储备的快速增长. 2015年8月, 央行下发了《中国人民银行关于加强远期售汇宏观审慎管理的通知》, 征收20% 无息外汇风险准备金, 增加了外汇投机成本, 降低外汇市场波动. 2016年5月, 央行发布的《关于全国范围内实施全口径跨境融资宏观审慎管理的通知》, 正式构建了全口径跨境融资宏观审慎管理框架. 2017年1月发布的《中国人民银行关于全口径跨境融资宏观审慎管理有关事宜的通知》, 提高了金融机构和企业跨境融资杠杆率, 便利了境内机构跨境融资, 促进了外债余额的增长. 2017年9月, 为了抑制外汇市场顺周期波动, 央行将外汇风险准备金调整为0. 2018年8月, 央行为应对人民币贬值, 将远期售汇业务的外汇风险准备金从0调整为20%. 2020年3月, 跨境融资宏观审慎调节参数由1调至1.25, 便利了境内机构跨境融资, 提高跨境融资风险加权余额上限. 2020年10月开始, 为了减少我国外债规模, 远期售汇业务的外汇风险准备金率从20%下调为0. 同年12月, 金融机构的跨境融资宏观审慎调节参数由1.25调至1. 2021年1月, 企业的跨境融资宏观审慎调节参数也由1.25下调至1, 同月, 境内企业境外放款的宏观审慎调节系数由0.3上调至0.5, 这一系列的操作缓解了人民币升值压力. 2022年3月, 发布了《关于银行业金融机构境外贷款业务有关事宜的通知》, 宏观审慎调节参数设置为1.
第三类是流动类政策工具, 本文考虑了存贷比要求(LDR)、流动性覆盖率(LCR)和净资产稳定比例(NSFR)这三种政策工具. 存贷比要求是银行贷款总额与存款总额之比. 在我国金融监管史上, 存贷比监管占据重要地位, 对商业银行具有巨大影响. 1994年, 中国人民银行发布《关于对商业银行实行资产负债比例管理的通知》, 规定存贷比不得超过75%. 1995年《中华人民共和国商业银行法》发布, 将其作为法定指标. 2015年8月, 全国人大常委会正式通过修改商业银行法的决定, 废除存贷比不超过75%的规定, 并将存贷比作为流动性监测指标, 至此, 在银行业执行了20年的监管指标才正式退出历史舞台. 在这20年间, 虽然75%的上限规定没有变动, 但具体的测算方法随着经济金融状况的变化调整了5次.
流动覆盖率是指无变现障碍的优质流动性资产与未来30天现金净流出之比, 由《巴塞尔协议Ⅲ》设定, 用于衡量银行短期流动性风险. 我国2014年3月实施的《商业银行流动性风险管理办法(试行)》正式引入流动性覆盖率作为流动性风险监管指标, 规定资产规模在2000亿元(含)以上的商业银行的流动性覆盖率不低于100%. 要求在2018年底前达到, 在过渡期2014–2017年底前分别达到60%、70%、80%、90%. 2015年12月发布的《商业银行流动性覆盖率信息披露办法》要求2017年起, 实施高级法的银行需披露季内每日数值的简单算术平均值, 并同时披露该平均值所依据的每日数值的个数, 这又对使用高级法的银行提出了新要求. 2021年3月《证券公司短期融资券管理办法(修订征求意见稿)》规定发行券商的流动性覆盖率应持续高于行业平均水平.
净稳定资金比率指银行可用的稳定资金来源与业务所需的稳定资金来源之比, 由《巴塞尔协议Ⅲ》设定, 衡量银行较长期限的流动性风险. 我国于2018年7月实施的《商业银行流动性风险管理办法》中引入净稳定资金比例监管指标, 要求不低于100%, 适用于资产规模在2000亿元(含)以上的商业银行. 2019年3月, 《商业银行净稳定资金比例信息披露办法》要求商业银行按半年度的频率披露最近两季度的净稳定资金比例相关信息, 进一步加强了商业银行的流动性风险管理.
第四类是其它类政策工具, 包括贷款集中度限制(CONC)、银行间相互敞口限制(INTER)和其他(OTHER). 贷款集中度限制是指对某一行业、集团或客户的授信额度占银行资本净额的比重限制. 《巴塞尔协议Ⅲ》要求商业银行应重视两类集中度风险, 即客户集中度风险和行业集中度风险. 我国1996年《关于印发商业银行资产负债比例管理监控、监测指标和考核办法的通知》中规定单一客户集中度不得高于10%, 最大十家客户集中度不得超过50%. 2006年1月施行的《商业银行风险监管核心指标(试行)》规定单一集团客户集中度不高于15%, 单一客户集中度不高于10%. 2012年修订的《商业银行资本管理办法(试行)》中也提出要求银行应充分考虑客户、行业、信用等级等各类集中度风险. 2021年1月, 《关于建立银行业金融机构房地产贷款集中度管理制度的通知》分档设置了银行贷款中房地产贷款占比和个人住房贷款占比上限. 2021年2月, 《关于进一步规范商业银行互联网贷款业务的通知》规定商业银行与合作机构共同出资发放互联网贷款的, 单一合作方发放的本行贷款余额不得超过本行一级资本净额的25%. 2022年1月, 《关于保障性租赁住房有关贷款不纳入房地产贷款集中度管理的通知》明确了关于保障性租赁住房项目发放的有关贷款不纳入房地产贷款集中度管理.
银行间相互敞口限制目的是防范金融机构间的风险传染. 随着我国金融机构同业业务的快速发展, 银行间的风险敞口大幅度增加, 风险的关联性急剧上升. 2014年4月发布《关于规范金融机构同业业务的通知》和2018年5月出台的《商业银行大额风险暴露管理办法》对银行间的风险关联性进行了一定的限制.
此外, 在我国金融监管实践中, 还存在着鼓励或规范银行与信托、证券、基金等合作进行金融创新的各种管理规定与办法. 这些管理规定与办法通过影响表内业务与表外业务之间的转移直接影响宏观审慎政策工具的事实约束力, 由于其影响较大, 不能忽略. 如2012年10月和11月颁布的两法一则《证券公司客户资产管理业务管理办法》《证券公司集合资产管理业务实施细则》和《基金管理公司特定客户资产管理业务试点办法》, 使得银行信贷业务由表内信贷大幅扩展至表外信贷, 大大弱化了宏观审慎政策工具的监管效果. 2016年7月开始出台的一系列金融监管政策, 则强化了宏观审慎政策工具的监管. 本文将这些规定与办法及其它有重要影响的政策变动列为其它.
采用Akinci and Olmstead-Rumsey (2018)的宏观审慎指数构建方法, 本文以2000年1月为基准, 基于以上四类政策工具的使用情况构建了自2000年以来我国的宏观审慎政策指数. 首先, 针对每种政策工具, 生成月度哑变量, 即LTV
1每个哑变量在各时期的取值以及MPI
2.2 我国宏观审慎政策使用情况和发展脉络分析
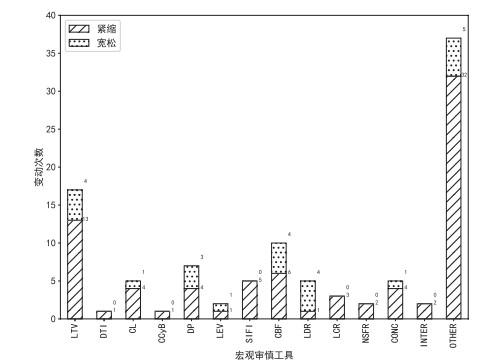
图1
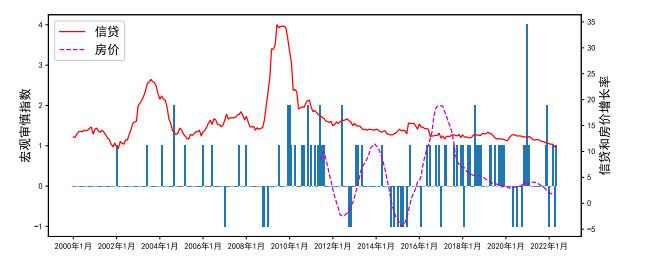
图 2为我国宏观审慎指数从2000年1月到2022年5月的时间序列图. 从图 2中可见, 2008年金融危机前, 我国宏观审慎政策使用次数并不频繁. 2003年1月, 我国信贷增长率快速上升, 4月, 一行三会监管框架建立, 金融监管体系平稳有序地从无到有逐步构建. 与此同时, 信贷增速得到有效控制, 信贷增长保持稳定直至2008年底. 为了应对全球金融危机, 2008年11月我国出台四万亿计划, 逆周期的宏观审慎政策开始呈宽松状态, 信贷增速随之迅速增加, 2009年10月信贷增长率接近35%. 鉴于信贷快速增长可能带来系统性风险, 管理当局于2009年12月开始采取一系列措施加强审慎监管, 以维护金融稳定. 在这一系列监管措施下, 信贷增速快速回落到原来水平. 2012年下半年, 为应对经济下行的压力, 宏观审慎政策转为宽松, 金融自由化浪潮开启. 2012年10–11月, 监管当局颁布了《证券公司客户资产管理业务管理办法》《证券公司集合资产管理业务实施细则》及《基金管理公司特定客户资产管理业务试点办法》, 这两法一则, 使得银行信贷业务由表内信贷大幅扩展至表外信贷, 信用创造从银行扩展至影子银行, 大大弱化了宏观审慎政策工具的监管效果, 监管力度明显放松. 这期间, 信贷增速维持稳定, 但房价增速却迅速上升. 2013年3月, 监管当局出台了《关于规范商业银行理财业务投资运作有关问题的通知》, 旨在从总量上控制影子银行的快速扩张, 监管趋紧. 房价增速于2013年12月开始迅速回落. 2014年9月930新政出台, 贷款估值比指标放松, 宽松的监管状态维持至2016年6月. 这期间, 房价增速迅速攀升, 金融乱象丛生, 防范系统性风险开始变得迫切. 随着2016年7月"新八条底线" 的出台, 整治金融乱象的序幕开始拉开, 一系列金融监管政策出台, 我国进入金融严监管期, 强调守住不发生系统性风险的底线, 房价增速开始回落, 信贷增速保持平稳. 2020年以来, 为了应对疫情带来的冲击, 动态拨备等监管指标进行了一些宽松性的调整. 整体来说, 宏观审慎监管框架越来越健全, 各项宏观审慎政策工具逐步平稳、有序地纳入宏观审慎监管框架中.
图2
3 中国系统性风险指数SRISK的测度与分析
估计系统性金融风险有两种思路, 一种思路是描述单个金融机构风险对系统风险的贡献度, 着重于构建风险在金融机构之间的传染效应, 如CCA (Lehar (2005)), CoVaR (Adrian and Brunnermeier (2014))等. 这一思路更适合于进行金融机构间风险相互传染的微观分析, 但不能直观地反映整个金融系统所面临的系统性风险. 另一种思路强调在市场处于不利条件时, 单个金融机构所面临的期望资本短缺. 该思路认为在经济状况较好的时期, 单个金融机构出现资本短缺时, 可能会被其他机构并购, 或有新的资金注入, 或进入有序的破产程序. 这些情况下, 由于该机构的资本短缺所带来的影响完全可以由其他机构来化解, 因此, 此时发生的单个金融机构的风险对整个金融系统的影响较小. 但当单个金融机构的资本短缺发生在整个金融系统出现资本短缺时, 它的风险将无法被化解与消化, 于是该金融机构的破产将会对整个金融系统, 甚至实体经济带来影响, 从而引发系统性风险. 第二种思路框架下, Brownlees and Engle (2017)提出了系统性风险指数SRISK. Brownlees and Engle (2017)指出SRISK是一具有前瞻性, 基于金融市场信息测度机构在发生系统性重要事件情况下预期资本短缺的指标. SRSIK将机构的资产负债表信息与市场信息结合在一起测度机构的条件资本短缺, 不仅利用了机构资产与负债的会计信息, 还利用了能提供机构未来价值的市场信息, 不仅与该机构股票的波动率和与市场的尾部相关性有关, 还与该机构的规模和杠杆率有关. Brownlees and Engle (2017)指出SRISK具有可加性, 所有机构的SRISK之和可作为反映整个金融系统的系统性风险指数, 它等于危机中政府救市所需资本总和. 此外, Brownlees and Engle (2017)还表明SRISK具有前瞻性, 所有金融机构SRISK之和可为实体经济的衰退提供早期预警信号. 因此, 本文采用SRISK作为金融稳定的代理变量, 进行宏观总量分析.
3.1 SRISK的定义与估计
SRISK
其中, LVG
其中,
本文采用DCC-GARCH模型估计MES. 记给定
其中,
其中, 指示变量
其中,
这里,
其中,
3.2 我国金融系统SRISK的估计
基于Brownlees and Engle (2017)的方法, 本文测度了我国金融系统2022年5月31日前上市的126家金融机构2000年1月到2022年5月期间的SRISK, 加总构建了金融系统的SRISK指数, 以观察系统性金融风险在时间维度的累积与发展. 126家金融机构包括银行44家, 证券56家, 保险6家, 其他金融机构20家. 金融机构的收益率为采用日度后复权收盘价计算出的对数收益率, 市场收益率采用上证A股综合指数计算. 借壳上市证券公司的上市时间定为借壳上市后的复牌时间. 由于金融机构的上市时间不统一, 所以数据是非平衡面板数据. 月度SRISK取月末SRISK值, 所有数据均来源于万得(Wind)数据库.
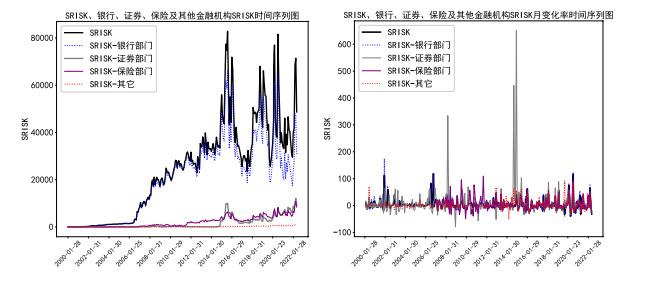
图 3为2000年2月到2022年5月期间, 我国金融部门总的SRISK以及四类金融机构SRISK的时间序列图及相应的月变化率时间序列图. 从图 3中可以看出, 我国金融部门SRISK在2007年以前很小, 2007年以后开始稳步增加. 这其中的一大原因在于2007年之前上市的金融机构数量较少, 尤其是系统性重要金融机构未上市. 2006年7月之前, 我国SRISK在2000以内. 中国银行于2006年7月份上市后, SRISK指数增加到3000以上. 随着工商银行、建设银行、中国人寿和中国平安等系统性重要金融机构的上市, 我国SIRSK指数于2007年9月底已达到11118. 因此, 本文将重点分析2007年到2022年间SRISK的变化. 图 3中显示, 2007年到2008年底, 受全球金融危机以及上市金融机构数量逐渐增加的双重影响, 我国SRISK迅速增加, 从2007年9月底的11118增加到2008年12月31日的18529. 随后我国SRISK呈平稳上升趋势, 从2009年1月的17259上升至2014年11月的33436. 这期间, 在2013年3月和6月底, SRISK出现了两次峰值, 分别达38123和39828, 这主要受钱荒事件的影响, 导致SRISK攀升. 进一步观察发现, 这两次峰值主要出现在银行系统, 保险机构于2013年6月底出现峰值, 但证券和其他金融机构的SRISK并没有相应的峰值出现. 2014年12月开始, 我国SRISK迅速上升, 从2014年11月底的33436上升到2015年8月底的82843. 这段时间恰巧是我国股市经历了暴涨和暴跌的"股灾" 时期. 普遍认为造成这次牛市与股灾的主要原因是加杠杆, SRISK成功地捕捉到了这一轮金融不稳定状态, 这期间SRISK迅速地上升具有很强的警示作用. SRISK在2015年8月底达到高点后逐渐下降, 到2015年底下降到44229. 但随后又迅速上升, 从2015年12月的44229短短1个月内迅速上升到1月底的71873, 这期间伴随着我国股票市场熔断机制的实施与停止. 随后, SRISK呈现逐渐缓慢下降的趋势, 到2017年7月下降到23557, 并一直保持低位至2018年1月. SRISK在这段时期下降的部分原因在于我国2016年第三季度开始采取金融严监管及降杠杆等措施. 从2018年2月开始, 我国SRISK又开始迅速上升, 到2018年10月达68009, 随后才开始逐渐下降. 这段时间SRISK的快速攀升刚好跟贸易战以来我国股市的大幅下跌相关联, 但SRISK开始上升的趋势要早于贸易战的发生. 2020年2月, 受新冠疫情的冲击, SRISK又出现新一轮快速上涨趋势, 从2020年1月的34804跃至3月的76996, 随后下降至6月的37940. 7–8月在新冠疫情二次爆发和中美关系紧张的双重风险压力下, SRISK又出现一轮高位震荡, 随后恢复为较为平稳的态势. 2022年3月, 受新冠疫情再次爆发的影响, SRISK于2022年3月又开始攀升, 4月达71407, 并维持高位于2022年5月底. 可见, SRISK指数可判别我国金融风险在时间维度上的累积. 以上结论与杨子晖等(2018)采用VaR, MES, CoVar等方法测度的我国金融部门的系统性风险所得到的相应样本期内的结论一致.
图3
从图 3还可以进一步看出, 银行系统的SRISK基本决定了整个金融部门的SRISK. 为了更深入地了解SRISK的主要贡献机构, 本文还从横截面维度分析了各机构对整体SRISK的贡献度. 2022年5月底, SRISK排名最大的前18个银行分别为工商银行、建设银行、交通银行、兴业银行、浦发银行、招商银行、中信银行、中国银行、平安银行、光大银行、华夏银行、邮储银行、宁波银行、农业银行、上海银行、江苏银行、北京银行和南京银行. 除广发银行未上市外, SRISK最大的前18个银行与我国发布的系统重要性银行一致. 此外, 中国平安、中国人寿、中国太保、中信证券、中国人保、国泰君安、华泰证券、中油资本等非银行金融机构也是我国SRISK指数贡献较大的机构. 可见, 从横截面维度看, SRISK可以识别我国系统性重要金融机构.
4 计量模型
本文采用了Rubin因果模型框架下发展出的宏观经济政策评估模型分析了我国宏观审慎政策对金融稳定的影响效应. 鉴于数据可得性与分析需求, 本文选择政策效应评估样本期起点为2007年4月. 由于我们要分析政策向前24期的影响效应, 因此政策效应评估样本期终点确定为2020年3月.与主流宏观经济政策分析的结构性模型相比, 本模型的主要优势在于建模自由度较大, 不需要对整个经济体系进行建模, 仅需对政策的选择机制进行建模. 同时, 在此分析框架下, 模型有效性检验可以转化为条件独立性检验, 从而可以对评估方法的适用性进行有效的统计检验. Angrist and Kuersteiner (2011)还进一步论证了该框架下提出的动态处理效应是对宏观经济分析的核心工具脉冲响应函数的进一步深化与发展, 可得到与DSGE和SVAR等现代宏观经济模型等价的分析效果. 本文采用Angrist et al. (2018)和刘泽琴等(2022)使用的基于政策倾向性得分的逆概率加权模型, 采用机器学习法拟合政策倾向性得分, 通过倾向性得分的逆概率加权, 模拟一个随机分配机制, 从而进行政策效应的估计, 模型设定如下:
其中,
根据第2部分构建的宏观审慎政策指数MPI
由于我们无法观测到所有的潜在结果, 动态政策效应
4.1 政策倾向性得分的估计
本部分旨在拟合政策倾向性得分模型
由于我国关于宏观审慎政策的选择基于"相机抉择"而非"单一规则", 因此根据刘泽琴等(2022)对数据的分析, 本文同样选用了其最终保留的54个宏观经济变量作为预测变量集
2指标的具体说明及其描述性统计量留存备索.
本部分将2020年4月至2022年3月作为测试集, 分别采用多元惩罚逻辑回归模型, 支持向量机和随机森林来训练式(4)中的模型. 模型的性能评价指标为测试集上的预测准确率. 在模型训练过程中, 根据测试集上的预测准确率, 调整
4.2 条件独立性检验
为了检验条件独立性的识别条件是否满足, 本部分采用Cai et al. (2021)在Fang et al. (2020)的基础上提出的时间序列框架下基于辅助变量的统计检验量检验条件独立性假设是否成立, 即
5 宏观审慎政策效应分析
本部分以中性宏观审慎政策
5.1 宽松性宏观审慎政策效应
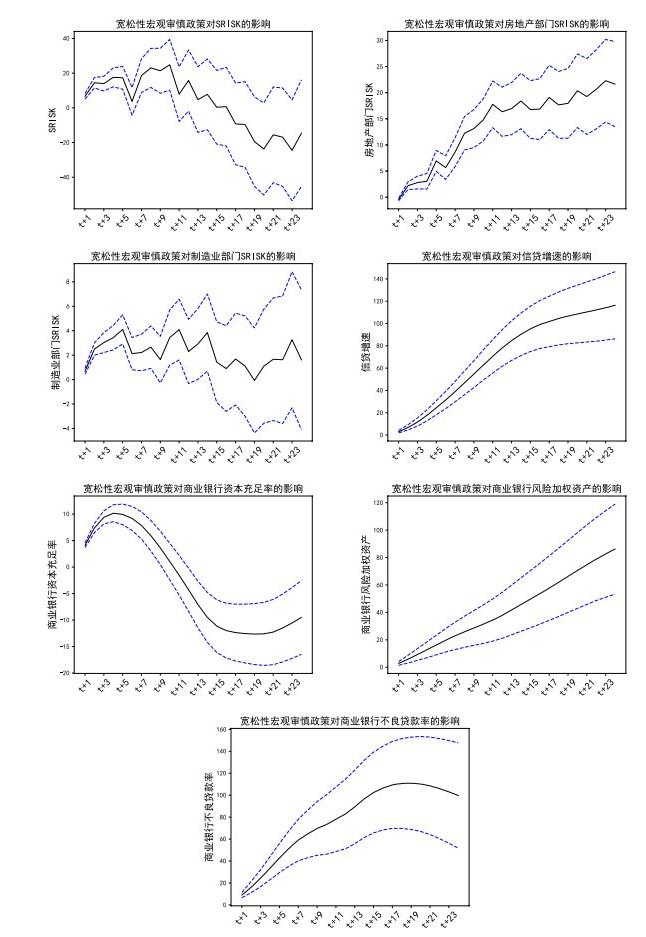
图 4报告了宽松性宏观审慎政策的影响效应, 其中, 实线代表具体目标变量向前24期的累积动态处理效应, 两条虚线代表累积动态处理效应95%的置信区间, 置信区间采用Bootstrap构建. 从系统性金融风险来看, 宽松性宏观审慎政策实施初期, SRISK的月变化率有所上升, 但保持平稳, 11期后SRISK的月变化率开始呈下降趋势, 并在24期内的累积影响效应不显著. 从系统性金融风险跨部门传染方面来看, 宽松性宏观审慎政策会显著提高房地产部门SRISK的月变化率, 政策实施11期后影响效应开始变小, 曲线走势较为平坦, 但在24期内的累积影响效应显著为正. 宽松性宏观审慎政策对制造业部门SRISK月变化率则基本无明显趋势性影响, 在24期内的累积影响效应不显著. 可见, 宽松性宏观审慎政策对房地产部门SRISK的影响效应大于对金融部门SRISK的影响效应, 但对制造业部门SRISK却无明显趋势性影响. 从宏观审慎政策对信贷传导渠道中重要中间变量的影响来看, 宽松性宏观审慎政策会显著提高信贷增速、商业银行风险加权资产同比增速和不良贷款率同比增速, 并且在政策实施的24期内累积影响效应均为正. 商业银行资本充足率的同比增速在宽松性宏观审慎政策实施4期后开始快速掉头向下, 这种下降趋势于政策实施17期后开始减弱, 并于20期后有所反弹, 但24期内的累积影响效应均为负. 以上关于宽松性宏观审慎政策对信贷渠道中间变量影响的结论, 除不良贷款率外, 与刘泽琴等(2022)得出的结论均一致. 在刘泽琴等(2022)的分析中, 宽松性宏观审慎政策对不良贷款率的影响并不显著, 本文延长样本期后, 估计结果显示会提高不良贷款率同比增速.
图4
综上所述, 宽松性宏观审慎政策会加大信贷渠道中间变量的风险, 这些风险主要传导至房地产部门, 导致房地产部门的SRISK显著提升, 但对金融部门系统性风险在24期内的累积影响效应不显著, 风险也没外溢至制造业部门.
5.2 紧缩性宏观审慎政策效应
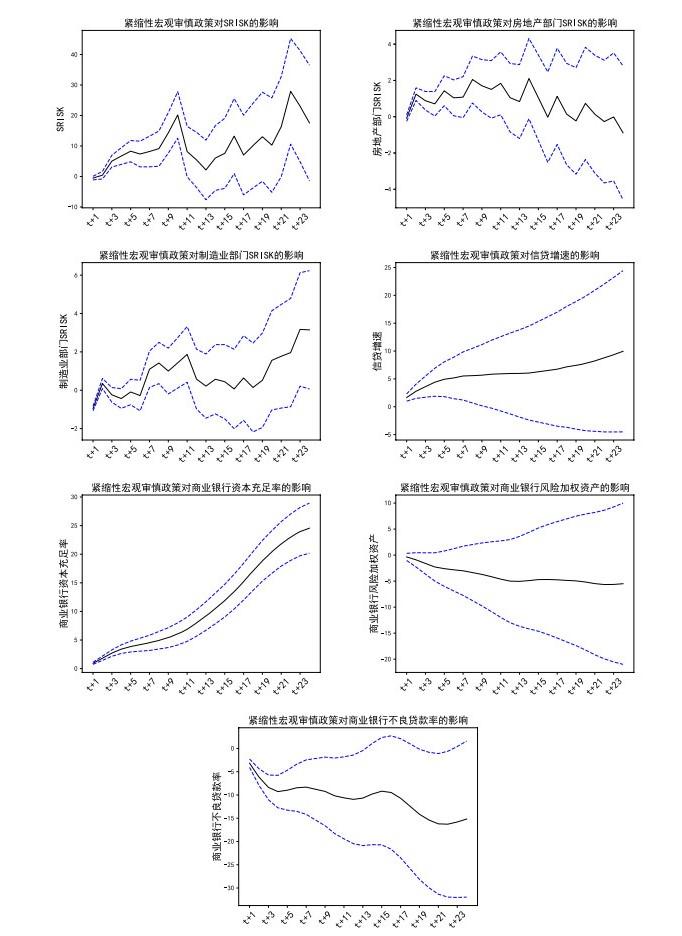
图 5报告了紧缩性宏观审慎政策对目标变量的影响效应. 从系统性金融风险来看, 紧缩性宏观审慎政策对SRISK无明显趋势性影响, 在政策实施前期会提高SRISK的月变化率, 11期后政策的累积影响效应不再显著. 从系统性金融风险跨部门传染方面来看, 紧缩性宏观审慎政策在政策实施前6期会提高房地产部门SRISK, 但影响效应很小, 从整体趋势上看, 有较弱的下降影响趋势, 但24期内的累积影响效应并不显著. 紧缩性宏观审慎政策对制造业部门SRISK的月变化率无显著影响. 从宏观审慎政策对信贷传导渠道中重要中间变量的影响来看, 紧缩性宏观审慎政策对信贷增速和商业银行风险加权资产同比增速无显著影响, 但会显著提高商业银行资本充足率同比增速, 并在政策实施的24期内累积影响效应为正. 紧缩性宏观审慎政策在政策实施前期会显著降低不良贷款率, 但在14期后政策的累积影响效应不再显著. 以上关于紧缩性宏观审慎政策对信贷渠道中间变量影响的结论与刘泽琴等(2022)的结论基本一致.
图5
可见, 紧缩性宏观审慎政策除了会显著提高商业银行资本充足率同比增速外, 对信贷渠道其他中间变量基本无显著影响, 进而对金融部门、房地产部门及制造业部门的SRISK也无明显影响.
6 结论与政策建议
本文采用Rubin因果效应框架下的现代宏观经济政策评估模型估计了我国2007–2020年宏观审慎政策对金融稳定的影响效应. 研究发现, 宽松性宏观审慎政策会加大信贷渠道中重要中间变量的风险, 这些风险主要传导至房地产部门, 导致房地产部门SRISK的显著提升, 而对金融部门系统性风险的累积影响并不显著, 风险也没外溢至制造业部门. 紧缩性宏观审慎政策除了会显著提高商业银行资本充足率同比增速外, 对信贷渠道其他中间变量基本无显著影响, 进而对金融部门、房地产部门及制造业部门的SRISK也无明显趋势性影响.
根据以上结论, 本文对宏观审慎政策提出如下政策建议: 1) 需进一步深化对系统性金融风险测度指标的研究. 系统性金融风险是宏观审慎政策制定与实施的靶向目标, 不同的测度指标反应风险的不同方面. 本文研究表明宽松性宏观审慎政策会加大信贷渠道中间变量的风险, 但对金融部门系统性金融风险指数SRISK在24期内的累积影响效应却不显著. 可见, 对宏观审慎政策目标"金融稳定" 代理变量的选择可直接影响政策评价结果. 本文使用了Brownlees and Engle (2017)提出的系统性风险指数SRISK来测度系统性金融风险, 一方面金融机构与整个金融市场的极端风险关联性LRMES可反映市场波动对金融稳定的影响. 另一方面SRISK
参考文献
宏观审慎政策有效性研究
[J].
A Study on the Effectiveness of Macro-Prudential Policies
[J].
我国系统重要性金融机构的识别与监管——基于系统性风险指数SRISK方法的分析
[J].
Identification and Regulation of China's Systemically Important Financial Institutions——Analysis Based on the Systemic Risk Index SRISK Method
[J].
中国宏观审慎政策工具有效性研究
[J].
Research on the Effectiveness of China's Macro-prudential Policy Tools
[J].
货币政策和宏观审慎双支柱调控框架的政策效应
[J].
Estimation of the Effects of the Two-pillar Regulatory Framework of Monetary and Macro-prudential Policies
[J].
宏观审慎政策的协调与搭配: 基于中国的模拟分析
[J].
Coordination and Matching of Macro-prudential Policies: A Simulation Analysis Based on China
[J].
双支柱调控的金融稳定效应研究
[J].
The Financial Stability Effects of the Two-pillar Adjustment
[J].
宏观审慎政策效应及其与货币政策关系研究
[J].
Effect of the Macro-prudential Policy and the Relationship between Monetary Policy and Macro-prudential Policy
[J].
我国金融机构系统性金融风险度量与跨部门风险溢出效应研究
[J].
Research on Systemic Risk Measures and Cross-sector Risk Spillover Effect of Financial Institutions in China
[J].
金融政策对金融危机的响应——宏观审慎政策框架的形成背景、内在逻辑和主要内容
[J].
Financial Policy Response to Financial Crisis——Forming Background, Internal Logic and Main Content of Macro-prudential Policy Framework
[J].
Capital Shortfall: A New Approach to Ranking and Regulating Systemic Risks
[J].
CoVaR
[J].
How Does Credit Supply Respond to Monetary Policy and Bank Minimum Capital Requirements?
[J].
How Effective Are Macroprudential Policies? An Empirical Investigation
[J].
Causal Effects of Monetary Shocks: Semiparametric Conditional Independence Tests with a Multinomial Propensity Score
[J].
Semiparametric Estimates of Monetary Policy Effects: String Theory Revisited
[J].
SRISK: A Conditional Capital Shortfall Measure of Systemic Risk
[J].
Comparative Assessment of Macroprudential Policies
[J].
The Use and Effectiveness of Macroprudential Policies: New Evidence
[J].
An Alternative Test for Conditional Unconfoundedness Using Auxiliary Variables
[J].
On the Role of the Propensity Score in Efficient Semiparametric Estimation of Average Treatment Effects
[J].
Efficient Estimation of Average Treatment Effects Using the Estimated Propensity Score
[J].
A Generalization of Sampling Without Replacement from a Finite Universe
[J].
Macroprudential Policy, Countercyclical Bank Capital Buffers, and Credit Supply: Evidence from the Spanish Dynamic Provisioning Experiments
[J].
Measuring Systemic Risk: A Risk Management Approach
[J].
Statistical Analysis and Evaluation of Macroeconomic Policies: A Selective Review
[J].
The Central Role of the Propensity Score in Observational Studies for Causal Effects
[J].