现代经济学广泛使用了定量分析方法. 在很多人的印象中, 定量分析工具主要是经济数学中的微积分和线性代数. 微积分用来解决数学优化问题, 很多求极值的问题, 例如效用最大化, 利润最大化或者成本最小化, 都可以转成一个数学优化问题并用微积分求解. 线性代数可用于求解线性联立方程, 比如说一般均衡, 多种商品的需求分别等于供给, 这种联立方程的求解就需要用到线性代数. 所以, 微积分和线性代数在经济学的广泛使用, 大家都比较熟悉.

事实上, 经济数学还有一个重要的组成部分, 即概率论与统计学. 为什么概率论是经济数学的重要组成部分?原因很简单, 现代经济学主要是研究在不确定性的市场条件下如何有效地和公平地配置有限的稀缺资源. 描述不确定性、不确定性带来的风险以及经济主体在不确定市场环境下的决策行为, 最好的数学工具是概率论.

另一方面, 过去40年来, 现代经济学发生了所谓的"实证革命" (Angrist et al. (2017)). 新古典经济学的主要分析方法是建立一些理论假设(如理性经济人假设), 在此基础上通过数学推导来构建经济理论, 这种分析方法现在仍很有用, 但是40年来, 现代经济学最主要的研究方法已转变为以经验研究为主, 即以数据特别是经济观测数据为基础, 应用统计学的推断方法进行实证研究. 这种实证研究将经济理论与经济现实连接在一起, 检验数据是否有证据支持经济理论. 所谓的统计推断方法, 在经济学就是计量经济学, 计量经济学是现代经济学实证研究的最主要方法论, 它的数学基础是概率论与数理统计学. 这是概率论与统计学成为经济数学重要组成部分的另一个主要原因.

这篇文章将通过一些典型的经济学、金融学实例说明概率论与统计学如何应用于经济学分析. 我们将挖掘概率论与统计学的一些最基本的概念、方法、工具的经济含义及其经济应用, 包括概率论与统计学的理论、方法与工具的可解释性. 我们不能只是简单、机械地把概率论与统计学的方法与工具应用于经济研究中, 而是必须清楚概率论与统计学的基本概念、方法与工具的经济含义, 以及它们成立的前提和适用的范围. 这些构成了对概率论与统计学最基本的概念、方法与工具的经济解释. 可解释性是理解和应用定量分析方法的重要条件. 本文大部分经济学、金融学应用例子取自洪永淼(2021)的《概率论与统计学(第二版)》一书, 但将聚焦于讨论概率论与统计学在经济学中的应用以及它们的经济解释.

概率论一个最基本的概念是某个事件发生的概率. 概率有两个基本解释, 一个是基于相对频率的客观解释, 另外一个是主观解释. 客观概率的解释建立在大量随机实验的基础之上. 在大量相同且互相独立的随机实验当中, 某事件出现的相对频率所趋于的极限就叫做该事件的概率. 这种解释建立在大量相同的独立随机实验的基础上, 单独一次实验, 不能显示概率的真正含义. 这种客观概率的解释在实际应用中得到了广泛的认可, 但在经济分析中, 有一些情形, 不可能会出现大量相同的随机实验. 特别是某些事件可能出现的次数就很少, 比如说极端的市场波动或冲击, 像2001年美国的"9$ \cdot $11"事件, 2003年的"非典"事件, 2019年的新冠肺炎疫情. 这些都属于所谓的"黑天鹅事件". 在这种情况下基于相对频率的概率解释会遇到困难, 特别是一些重要的事件, 其发生的社会经济条件每次都不一样, 这样假设在相同条件下进行大量的随机试验这个前提就不成立. 为了解决这个问题, 概率学家提出了另一种解释, 即所谓的主观概率解释. 在经济学, 这主要就是指经济主体认为某个事件出现的概率, 是对事情发生的可能性的一种主观判断.

主观概率的解释让很多概率论初学者感到难以理解, 特别是主观判断会因人而异. 甚至有人可能还会怀疑概率论在经济学的应用到底有多大的科学性, 因为将一个事件出现的概率解释为一种主观的意念, 与客观发生的可能性是两回事. 但是, 主观概率作为经济学的一种定量分析工具, 有广泛的应用. 下面我们举几个例子.

宏观经济学有一个非常著名的理论叫理性预期(rational expectations)学派, 其主要假设是经济主体关于某个随机事件的主观期望和该事件出现的客观期望(也称数学期望)是相等的, 即主观期望和客观期望是一致的(参见Muth (1961)). 如果用数学语言表示, 主观期望就是以主观概率为权重, 对某个随机经济事件的结果进行加权平均. 这里, 主观概率、主观期望成为一个基本的定量分析工具. 我们现在经常听到"预期管理", 如"稳预期". 什么是预期管理?在不确定性的环境下, 经济主体对未来的不确定性有一定的预期, 这种预期会影响到他们当下的经济行为, 包括投资与消费. 中央银行或者政府部门通过一系列的政策手段和工具, 试图改变经济主体对未来的预期, 以达到稳定经济、促进消费和投资等目的, 这就是预期管理. 预期管理其实就是不确定性管理.

另一个例子是金融学中的衍生产品定价(参见Hull (2017)). 所谓金融衍生产品就是金融避险工具, 在市场出现激烈波动时, 可以避免投资者遭受巨额损失. 那么如何对衍生产品进行定价呢?金融衍生产品一般都会定义一个支付函数(payoff function), 同时有一个重要概念, 就是所谓的风险中性概率(risk-neutral probabilities). 在一个无套利机会的完全市场中, 任何一个金融衍生产品的价格等于支付函数乘以风险中性概率的加权平均. 风险中性概率有什么经济含义呢?这是经过投资者风险厌恶态度调整之后的概率分布. 换句话说, 风险中性概率反映了一个厌恶风险投资者对某个事件可能出现的概率分布的主观判断以及愿意支付的溢价, 这种主观判断本身反映了投资者的风险厌恶态度或心理恐慌情绪, 它和真实世界或客观概率(physical probabilities)是不一样的. 一个是厌恶风险的投资者认为的某个事件可能出现的概率分布与愿意支付的溢价, 一个是某个事件客观发生的概率分布, 两者本身存在差距, 差距的大小决定金融衍生产品价格的高低. 风险中性概率与客观概率偏离得越大, 对衍生产品避险需求越强, 因此衍生产品的价格就更高. 风险中性概率是一个金融衍生产品定价的重要工具, 可以在没有投资者效用函数信息的条件下, 获得风险调整后的价格. 根据现代金融理论(Breeden & Lizenberger (1978)), 从现有衍生产品价格可以推导出风险中性概率, 这样我们就可以用它来定价任何一种新的金融衍生产品. Gisiger (2010)对风险中性概率提供了详细的经济解释.

最后一个主观概率的例子是宏观经济概率密度预测(Diebold et al. (1999)). 美国费城联邦储备银行定期发布专业预测者调查(Survey of Professional Forecasters), 调查问卷是类似这样的: 你认为美国下个季度的GDP增长率在$ -5\%\sim-4 $%这个区间的概率有多大, 在$ -4\%\sim-3 $%这个区间的概率有多大, 在零增长到1%这个区间概率有多大, 在$ 1\%\sim2 $%这个区间概率有多大$ \cdots $, 这样每个调查者实际上给出了一个关于GDP增长的主观概率分布预测. 同样地, 对通货膨胀率, 被调查者也给出了主观概率分布预测. 这种概率分布预测对美联储分析宏观经济走势, 进行精细化宏观调控, 提供了非常有价值的信息.

在博弈论、行为经济学和实验经济学中, 主观概率也是一个基本的定量分析工具. 贝叶斯统计学中所谓的先验概率和后验概率也是主观概率. 主观概率虽然不一定是经济事件发生的客观概率, 但它是一种很有用的定量分析工具.

概率分布一般是由累积分布函数(cumulative distribution function, CDF)来刻画, 定义为$ F(x) = P(X\leq x) $, 描述一个随机变量$ x $取值小于等于某一个值$ x $的概率. 当数值变化时, 概率随之而变. 从数学上讲, 累积分布函数完整地刻画一个随机变量的概率分布.

下面我们举例说明累积分布函数可用来分析一些经济学最重要的问题. 第一个例子是洛伦兹曲线(Lorenz curve). 收入分配是经济学一个最基本问题. 如何测度收入分配特别是收入分配不均等及其演化趋势, 一直是经济学研究中一个非常重要的问题.

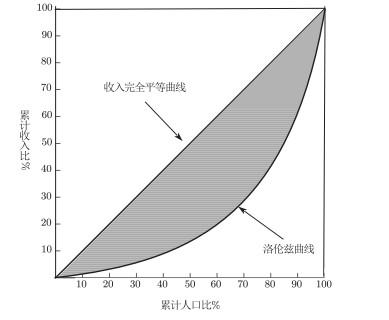
如图 1所示, 洛伦兹曲线的横轴代表人口百分比, 取值0到1, 纵轴代表收入占比, 也是0到1, 这样45度线就代表绝对均等收入分配. 如果一个随机变量是收入, 我们刻画收入小于等于某一个收入水平的人口比例, 则这个人口比例就相当于一个累积概率函数的概念. 洛伦兹曲线全面且直观地刻画了整个社会的收入分配. 如果随着收入水平的提高, 人口比例一直是0, 直至最高收入时, 人口比例突然跳成1, 则这一个90度直角线代表最不均等的收入分配, 即一个人占有整个社会所有财富或者所有收入. 现实观测到的洛伦兹曲线介于直角线和45度对角线之间, 越靠近45度对角线表示社会收入分配越均等, 越靠近90度直角线就意味整个社会收入不平均的程度越高.

洛伦兹曲线包含的信息非常丰富, 但是为了简单起见, 我们常用基尼系数(Gini index)刻画收入不均等程度. 什么是基尼系数? 45度对角线和洛伦兹曲线两者之间的图形面积与45度线下方三角形面积的比例就叫基尼系数. 当收入变量非负数时, 基尼系数取值在0到1之间. 如果收入绝对不平均, 相应的洛伦兹曲线为90度直角线, 其与45度对角线的面积刚好等于三角形的面积, 这时候基尼系数等于1, 代表收入不均程度最大. 如果洛伦兹曲线与45度对角线重叠, 基尼系数等于0, 代表绝对平均的状况.

Krugman (1991)提出用空间基尼系数来测度经济活动在空间上的集中程度, 此时随机变量当然不再是收入. 在机器学习中, 基尼系数可作为测度分类精准度. 例如, 分类与回归树(classification and regression trees, CART) 算法在构建决策树中使用基尼系数作为一种不纯度度量(impurity measure) (参见Shobha & Rangaswamy (2018)).

另一方面, Hadar & Russell (1969)、Hanoch & Levy (1969)以及Rothschild & Stiglitz (1970)都提出用随机占优(stochastic dominance)的方法来评估不确定性的环境, 包括收入分配评估、社会福利评估以及投资组合评估等. Whang (2019)从计量经济学的视角和一个统一的分析框架出发, 提供了一个全面且最新的关于随机占优及其在经济学的应用的介绍.

所谓随机占优, 是通过比较两个累积分布函数的形状而定义的. 随机占优是一族概念, 包括一阶随机占优、二阶随机占优、三阶随机占优等. 例如, 如果对所有$ x $值, 有$ F(x)\leq G(x) $, 且存在至少一个$ x $值, 有$ F(x)< G(x) $, 则我们称分布$ F(x) $相对于分布$ G(x) $是一阶占优. 如果对所有$ x $值, 有$ \int_{-\infty}^{x}F(u){\rm d}u\leq\int_{-\infty}^{x}G(u){\rm d}u $, 且存在至少一个$ x $值, 有$ \int_{-\infty}^{x}F(u){\rm d}u<\int_{-\infty}^{x}G(u){\rm d}u $, 则我们称$ F(x) $相对$ G(x) $是二阶占优. 随机占优和经济主体的行为, 特别是厌恶风险的行为, 是密切相关的. 例如, 一阶随机占优意味差效用函数$ u(x) $具有未满足性(即$ u^{'} (x)\geq0 $)的经济主体会偏好一阶随机占优的分布. 如果经济主体是风险厌恶型的(即$ u^{'} (x)\geq0 $, $ u^{"} (x)<0 $), 那么他会偏好二阶随机占优的分布. 如果经济主体不仅是风险厌恶型的, 而且具有正偏度的偏好, 即$ u^{"'} (x)\geq0 $, 则他会偏好三阶随机占优的分布. 这样, 通过随机占优的概念, 我们可用累积概率分布将经济主体的风险态度刻画出来.

在统计学特别是生物统计学和卫生统计学中, 有一个所谓的生存分析(survival analysis)方法. 生存分析的一个重要概念是生存函数(survival function), 指一个事件发生后持续的时间$ Y_{i} $ (如新冠肺炎患者的存活时间)超过任意给定时数$ y $的概率, 即$ S(y) = 1-F(y) $, 其中$ F(y) $是随机变量$ Y_{i} $的积累分布函数. 另一个相关的重要概念叫危险函数(hazard function) $ h(y) $, 定义为某个事件(如患病)持续了一定时数$ y $后, 在$ y $这个时点结束的瞬时概率, 它与生存函数的关系为$ h(y) = -\frac{\rm d}{{\rm d}y}{\rm ln}S(y) = \frac{f(y)}{S(y)} $, 其中$ f(y) $是随机变量$ Y_{i} $的概率密度函数. 生存分析主要是对危险函数$ h(y) $建模, 刻画哪些解释变量会影响事件的持续时间, 如著名的Cox's (1972)比例危险模型. 除了生物统计学和卫生统计学外, 生存分析在经济学中也有广泛的应用, 如解释工人失业的持续时间、初创公司的成败以及贫困户脱贫的相关经济因素.

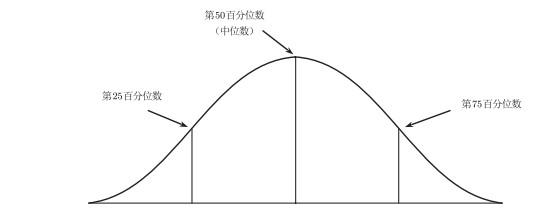
分位数把一个概率分布图分成两部分, 左边那一部分的概率等于某个值$ \alpha $, 其中$ \alpha{} $在0和1之间, 而剩下来的右边那一部分的概率就是$ 1-\alpha $. 如果$ \alpha{} $等于0.5, 整个概率被分成两个等半, 每部分的概率都是50%, 那个分值就是所谓的中位数(median). 例如, 如果$ \alpha $分别等于25%、50%、75%, 我们就得到不同水平的分位数, 称为四分位数(quartiles), 如图 2所示. 统计学中参数区间估计和参数假设检验所用到的临界值(critical values), 就是分位数的概念.

分位数在经济学中有哪些重要的应用呢?我们首先考虑中位数. 如果一个随机变量代表收入, 那么50%的人口的收入水平小于中位数收入, 而另外50%的人口的收入水平高于中位数收入. 这个概念比较接近我们常听到的中等收入群体的概念. 中国现在的中等收入群体(以中国典型的三口之家, 家庭年收入在10万元$ \sim $ 50万元之间为标准)大概有4亿人, 那么中等收入群体是如何定义的呢?每个国家可能有不同的定义. 美国"中等收入群体"常用的定义是三口之家的收入在中位数收入的2/3到中位数收入的两倍之间, 也就是说最低收入是中位数收入的2/3, 最高收入是中位数收入的两倍, 收入位于这二者之间的家庭就叫做中等收入群体.

上面提到, 基尼系数可以刻画整个社会收入不均等的程度, 但也存在严重的缺陷. 特别是, 两个不一样的收入分布的基尼系数可能是一模一样的. 例如, 在一个国家, 底层50%的人没有收入, 另外50%的人收入相同, 该国的基尼系数为0.5; 然而, 在另一个国家, 底层75%的人拥有25%的收入, 另外25%的人拥有75%的收入, 该国的基尼系数也是0.5. 这表明基尼系数只是对收入分配不均等的一种总体测度, 可能无法区分两个不同的收入分布. 有更好的方法吗?有, 就是分位数. 法国经济学家托马斯·皮凯蒂(2014)在其《21世纪资本论》中就提倡使用这种方法. 他指出基尼系数在刻画收入分配的重要缺陷, 主张使用分位数, 特别是用不同水平的分位数刻画一个经济体的收入不均等的程度以及财富分配不均等的程度. 比如, 收入最低的50%的这个群体, 其收入占比是多少?如何随时间在变化?另外, 收入最高的1%的人口的收入占比有多大?如何随时间在变化?经济全球化以来, 世界主要国家收入不均等的程度一直在扩大. 其主要标志体现在收入水平较低的50%人口的收入占GDP的比重一直在下降, 而收入最高的1%群体的收入占GDP的比重的一直在增加, 这意味着整个社会的收入越来越集中在少数人手里. 这种用分位数来刻画收入不均衡的方法, 避免了基尼系数可能区分不了不同分布的缺陷. 皮凯蒂也因此被称为"1%先生".

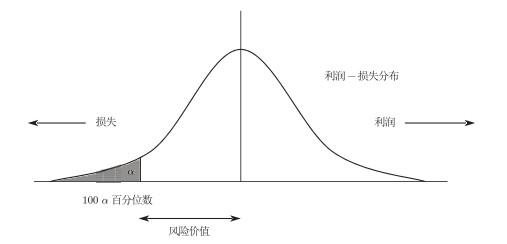
以上例子都跟收入分配有关. 分位数也可以用来刻画金融风险, 比如说J.P. Morgan在20世纪90年代提出了一个量化风险管理方法论—风险计量学(RiskMetrics). 金融投资在一定时期的收益一般会随市场的波动而变化, 有时候增加, 有时候减少, 有时候是正收益, 有时候是负收益. J.P. Morgan (Longerstaey & Spencer (1996)) 提出用一个单一的货币度量指标来刻画某一个金融投资(如投资组合)所面临的市场风险. 这里, 随机变量是投资收益率, 其分布就是收益率的概率分布, 而这个指标叫做风险价值(Value at Risk, VaR).

风险价值如何定义呢?风险价值其实就是一个分位数, 把收益率的整个概率分布分成两部分, 其中左部分的概率等于$ \alpha{} $, 右部分的概率等于$ 1-\alpha{} $, $ \alpha{} $可以是1%、5%或者10%. 风险价值虽然是一个很有趣的金融名词, 在金融业中已被广泛使用, 但它其实是分位数. 风险价值有什么经济含义呢?假设随机投资收益率的损失超过某个值VaR的概率等于$ \alpha{} $, 即$ P(X_t<-{\rm VaR}) = \alpha $, 其中$ X_t $代表收益率, 那么VaR就叫做在水平$ \alpha{} $上的风险价值. 按照客观概率的解释, 假设有很多投资交易日, 那么大约有比例为$ \alpha{} $的天数, 收益率损失会超过VaR, 而另外有比例为$ 1-\alpha{} $的天数, 收益率要么为正, 要么损失会小于VaR. 比如, 当$ \alpha{} $等于1%, 损失超过VaR的概率是1%, VaR就是在1%水平上的风险价值. 如果一个金融公司手上拥有总量为VaR的现金或流动资产, 可以随时去应对任何意料不到的损失, 那么这个公司在99%的交易日中是安全的, 不会倒闭或破产, 只有1%概率, 损失会超过所拥有的现金或流动资产VaR. 在这种情况下, 要么破产重组, 要么需要找银行或者保险公司谈判. 有关VaR的系统介绍, 可参见Jorion (2006).

VaR概念被Adrian & Brunnermeier (2016)拓展为CoVaR概念, 用于测度金融市场的系统风险(systemic risk). 所谓系统风险是指由于一个或几个重要金融机构的风险扩散到整个金融市场, 导致整个金融体系出现重大风险. CoVaR可以用来测度一个或几个重要金融机构出现风险时对整个金融市场系统风险的影响, 以及当系统风险发生时对个别重要金融机构所面临风险的影响. Hong, Liu & Wang (2009)提出了一个基于VaR (事实上是CoVaR)的格兰杰因果检验方法, 检验不同资产或不同市场之间的极端风险溢出效应.

均值和方差是概率论两个重要的基本概念. 所谓均值是一个概率分布的位置中心, 而方差是指对中心位置的偏离度, 即刻画一个随机变量对均值的偏离度的大小.

均值和方差在经济学有广泛应用. 政治经济学有一个最基本的经济法则叫价值规律. 经济法则就是在一定的社会生产方式条件下, 特别是在一定的生产方式和交换方式的条件下, 必然会表现出来的某种客观要求或倾向. 马克思在《资本论》中发现, 价值规律是资本主义经济制度下发挥最基础作用的经济法则. 什么叫做价值规律呢?就是一个商品的价值是由生产这种商品的社会

生产平均劳动时间来决定. 显然, 劳动者生产的技能越高, 或社会劳动生产力越高, 那么生产一种商品的平均劳动时间就越少. 因此, 商品价值与生产商品的社会平均劳动时间成正比, 与社会生产力水平成反比.

投资组合(portfolio selection)理论是均值与方差在金融学的一个重要应用. Markowitz (1952)提出经典的投资组合理论, 其中, 投资收益率均值代表了投资组合的期望回报率, 方差则代表投资组合的风险. 通过最大化投资者的效用函数, 可以刻画期望回报率和风险两者之间的关系, 从而确定最佳投资组合权重. 一般来说, 如果风险越高, 期望回报率就需要越高, 才能补偿风险增加的部分.

Markowitz因提出投资组合理论而在1990年获得诺贝尔经济学奖. 从他的获奖感言中, 可看出概率论与统计学方法对现代经济学的影响. Markowitz (1991)说: "当年我在芝加哥大学进行经济学博士论文答辩时, Milton Friedman教授称投资组合理论不属于经济学, 因而我的论文不属于经济学范畴, 也就不能授予我经济学博士学位. 我知道他只是半开玩笑, 因为答辩委员会并没有花费太长的时间争论就决定授予我博士学位. 对于他的说法, 现在我也愿意承认, 当年博士论文答辩时, 投资组合理论并不是经济学的一部分, 但它现在是了. "

在金融学界和金融业界, 有一个名词叫做夏普比率(Sharpe ratio), 定义为投资期望超额回报率(即减去无风险利率后的回报率)与回报率标准差的比例, 可解释为每单位风险的预期超额回报率. 如果有两个或者两个以上的投资项目或者投资组合, 那么投资者将会挑选那个夏普比率最高的投资项目或投资组合.

在经典投资组合理论中, 方差被用以刻画投资组合的风险. 事实上, 虽然风险来源于不确定性, 但是经济或金融风险与经济主体的风险态度是密切相关的. 例如, 经济主体的风险厌恶态度可能具有不对称性, 即面对损失和收益, 或面对经济下行时的损失和经济上行时的损失, 其风险态度不一样. 这是所谓的前景理论(prospect theory; Kahneman & Tversky (1979)). 在这种情形下, 方差不能完全刻画风险.

为了分析在不确定性条件下风险厌恶型的经济主体的经济行为, 我们需要更一般的概率论工具. Rothschild & Stiglitz (1970)提出了一种刻画经济主体厌恶风险的概率分布, 叫做均值保持不变的扩散分布(mean-preserving spread), 它的意思是, 对风险厌恶型的投资主体来讲, 如果有两个分布, 它们的均值相等, 但其中一个概率分布向两边扩散, 那么风险厌恶型的经济主体会偏好那个比较集中的分布, 换言之, 厌恶风险的经济主体比较不喜欢那种波动较大的分布. 这里使用均值保持不变的概率分布来刻画经济主体的风险态度, 避免了用方差刻画风险的缺陷. 比如, 有可能存在两个不同的分布, 它们的均值和方差分别相等, 但均值保持不变的分布还是可以区分开来的.

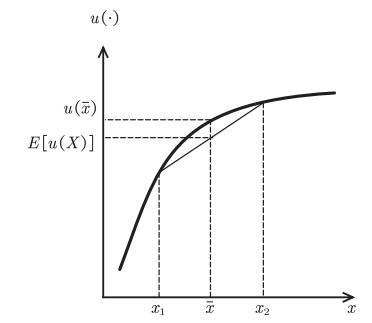
数学上有一个不等式叫做Jensen不等式. Jensen不等式是指, 如果有一个经济主体, 其目标函数是收益的一个凹函数(concave function), 那么它的目标函数期望值将会小于等于目标函数在平均收益这点的取值, 如图 5所示.

现在假设一个风险厌恶型的经济主体有两个选择, 一个是拥有确定的平均收入, 另外一个让他置身于一个不确定性的环境中. 那么风险厌恶型的人将偏爱获得平均收入, 也就是说在平均收入这一点上的目标函数值会大于不确定性条件下目标函数的期望值. 经济主体偏好平均收入, 而不愿意置身于不确定性的环境下, 这其实是保险理论的基础. 人们之所以愿意去缴纳一定的保险费, 是因为如果他有一个确定的平均收入, 那么他的目标函数值会大于处于不确定状态下的目标函数期望值. 因此, 风险厌恶型的人愿意让渡出一定的收入去买保险.

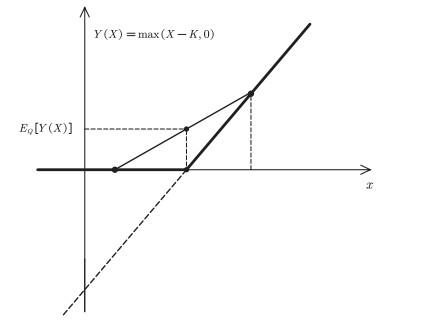
Jensen不等式的另外一个应用是金融衍生产品定价(参见Hull (2017)). 上文提到, 金融衍生品是一种金融避险工具. 这种避险工具通常假设一个非线性的支付函数. 比如欧式期权(European call options; 参见Black & Scholes (1973))是给投资者一种权利, 在合约到期时, 投资者拥有以事先定好的价格购买某只股票或资产的权力, 也可以不买. 显然, 在合约到期时, 如果股票或者金融产品的价格高于事先定好的买价, 这对投资者来说有利可图, 所以他会买; 反之, 如果股票或者金融产品的价格低于事先约定的买价, 投资者将会放弃购买的权利. 这种非线性的收入函数, 避免了极端下滑的市场风险. 从数学上说, 这种非线性支付函数其实是一个凸函数(convex function). 负的凸函数是一个凹函数. 应用Jensen不等式, 可以得到, 投资者在衍生产品条件下的期望回报率, 会高于没有衍生产品的期望回报率, 两者之差决定了金融衍生产品的价格水平. 这是金融衍生产品定价的理论基础, 参见图 6.

经典弱大数定律是指在独立同分布条件下, 一个随机样本的样本均值$ \overline{X}_n $会随着样本容量$ n $的增加而依概率趋于总体均值. 换言之, 样本均值趋于总体均值的概率, 随样本容量的增加而趋近1, 这就是弱大数定律. 简单地说, 大数定律就是在相同条件下进行多次的、互相独立的随机实验, 所有实验结果的平均值最终会稳定在一个极限, 这个极限就是总体均值. 换言之, 当样本容量很大时, 样本均值和总体均值几乎是一样的. 大数定律为我们理解总体均值的含义提供了很好的一个视角.

为了说明这一点, 我们考虑一个金融学例子. 金融学有一个购买并持有投资策略(buy-and-hold investment strategy), 是指一个投资者买下了一只股票或一个金融资产, 然后长时间持有它, 最后才把它卖出去. 如果我们想知道这一投资策略的日平均回报率有多高, 那么在持有期里, 将每天的收益率加总除以持有天数就可以得到日平均回报率, 这是样本均值. 如果持有期很长, 这个平均回报率就会以很大的概率无限趋近总体均值. 总体均值因此可以理解为长期市场回报率, 这是大数定理提供的一种经济解释.

大数定理的应用范围很广, 可以解释很多经济现象. 比如说, 中国银行业面临的一个非常重要的问题是众多的小微企业信贷风险比较高. 小微企业体量小, 抗风险能力较强, 可以抵押的资产或工具也不多, 所以银行一般不大愿意贷款给风险高的小微企业. 过去一段时间, 一些商业银行发明了一种中小企业联保制度, 即在某一个地区, 甚至是在相同的或者相关的行业中, 如果有中小企业想贷款, 那么这些企业可以三五家甚至更多的组成一个联保集团. 当这个联保集团的任何一家企业因为亏本等原因没有办法还贷时, 其他联保企业应该保证还贷. 这对银行来讲似乎风险降低了. 事实上, 在经济上行时, 这个联保制度不会出大的问题, 但一旦经济下行, 特别是若出现了区域性系统风险的或者行业性的经济不景气, 在同一个地区或者同一个行业的所有企业都会受到负面的冲击. 此时, 如果一家企业无法还贷, 而其他联保企业又必须替它还贷, 其结果是所有联保企业都可能被拉下水, 出现大面积破产或停产. 之所以会这样, 是因为联保制度破坏了企业之间的互相独立性, 而这是大数定律发挥作用的一个重要条件. 大数定律不一定要严格满足独立同分布条件, 企业之间可以存在一定的关联, 但是这种关联不能太强.

在独立同分布条件下, 一个随机样本的样本均值$ \overline{X}_n $会随着样本容量$ n $的增加而趋于总体均值, 即随着样本容量的增加, 样本均值和总体均值之间的差距越来越小, 最后趋于零. 事实上, 假设每个随机变量的方差是有限的, 那么在独立同分布条件下, 样本均值可以视为一些互不关联的小扰动的平均, 这些小扰动互相抵消, 因此随着样本容量的增加, 这些互不关联的随机变量的平均值, 其围绕总体均值的波动越变越小. 可以证明, 样本均值的波动, 如果用方差刻画的话, 等于总体方差除以样本容量$ n $, 即var$ (\overline{X}_n) = \frac{\sigma^2}{n} $, 其中$ \sigma^2 $为总体方差. 因此, 在独立同分布条件下, 样本均值的方差与样本容量成反比.

这个结果不但保证了大数定律的成立, 甚至金融学中所谓资本资产定价模型(capital asset pricing model, CAPM)也是基于这一统计抽样理论的基本结果. CAPM是指在一个无套利机会的完全市场中, 任何一个资产的期望回报率只能是补偿不可避免的系统风险的回报率. 个体资产的特质风险(idiosyncratic risk), 也就是只与每个资产或每个企业相关的风险, 不应该获得风险补偿. 为什么呢?因为我们可以构建一个包含很多资产的等权重的投资组合, 这个投资组合的回报率包含两部分, 一部分是不可避免的系统风险带来的回报率, 另外一部分是由所有资产的特质风险带来的平均回报率. 因为众多的特质风险互相抵消, 因此这一部分的风险, 如果用方差测度, 将随资产个数的增加而趋于0. 换句话说, 由于异质风险互相抵消, 这部分风险不用补偿. 另一方面, 不管资产个数有多大, 不可避免的系统风险这部分不会互相抵消, 因为系统风险对每个资产的冲击方向都是一致的. 因此在均衡状态下, 每个投资组合的期望回报率应该只是补偿不可避免的系统风险那一部分的回报率. 从这个例子可以看出, CAPM的理论基础是统计学, 即样本均值的方差随着样本容量增加而趋于0. 在金融学中, CAPM是由Sharpe (1964)、Lintner (1965)和Mossin (1966)等独立提出的.

样本均值的方差与样本容量成反比这个结果, 可直接推导出中心极限定理, 即如果将样本均值标准化, 则其概率分布将随样本容量的增加而趋于标准正态分布, 所谓标准化, 是指样本均值减去总体均值后除以样本均值的标准差. 标准化样本均值之所以趋于标准正态随机分布, 其主要原因就是样本均值的方差与样本容量成反比.

概率论与统计学有很多方法和工具可以刻画各种统计关系, 如相关关系和预测关系. 刻画统计关系的方法与工具很多, 如联合分布函数、条件分布函数、联合积矩(joint product moments)、各种相关性(correlations)等. 但是这些统计关系不是经济因果关系.

如果各种统计关系都不存在, 则称为统计独立性(statistical independence), 统计独立性的严格定义是两个随机变量之间的联合概率分布函数等于它们各自分布函数的乘积. 互相独立意味着不存在任何的统计关联.

统计独立性可以刻画市场有效性(efficient market hypothesis). 一个经典例子就是随机游走(random walk)模型在金融市场上的应用(参见Fama (1965)和Malkiel (1973)). 这个思想至少可以追溯到法国数学家Louis Bachelier 1900年的博士论文(参见Bachelier (2011)). 如果有一个金融市场, 其中每一天的资产回报率是互相独立的, 因此将来的回报率与历史的回报率互相独立, 我们无法用历史的回报率信息来预测将来回报率. 当一个市场达到这样的状态, 我们就说这个市场是有效的.

事实上, 在经济学中, 市场有效性并不意味着不同时期的回报率是互相独立的. 所谓市场有效性, 特别是弱式有效市场假说(weak-form of efficient market hypothesis), 是指不能用历史回报率信息预测未来的期望回报率. 更准确地说, 未来回报率相对于整个历史回报率的条件期望, 与历史回报率无关. 从时间系列分析的角度看, 如果未来回报率相对于历史回报率的条件均值与历史回报率无关, 那么未来条件期望回报率就无法用历史回报率信息来预测. 当然, 不能预测回报率条件期望并不意味未来回报率相对于历史回报率的条件高阶矩, 比如说它的条件方差, 也是不可预测的. 条件方差刻画市场波动大小, 一个有效市场的回报率的波动大小是可以用历史信息预测的. 一个著名的例子是Engle's (1982)的自回归条件异方差(autoregressive conditional heteroskedasticity, ARCH)模型.

因此, 虽然独立性意味着市场有效性, 但市场有效性的定义, 并不是由独立性刻画, 而是由条件期望或鞅差分(martingale difference sequence, MDS)来刻画. MDS是指给定历史信息的条件期望超额回报率(即回报率减去无条件均值后)在每个时期均为0. 事实上, 市场有效性更一般的定义是, 扣除风险补偿或风险溢价后的超额回报率为MDS, 即扣除风险补偿后的超额回报率是无法预测的, 资产回报率本身可能是可以预测的, 因为风险溢价可以预测, 这与市场有效性并不矛盾. 可以看出, 概率论的一些相关但又不同的重要概念, 在刻画市场有效性时, 既有联系, 也有区别.

统计推断主要有两大任务, 一个是参数估计, 另一个是参数假设检验, 所谓参数检验通常是指一个统计模型(如线性回归模型)包含若干未知参数值, 我们想检验这些未知参数值是否满足一定的约束条件, 比如说某个参数等于0. 参数约束就构成了一个统计假设(hypothesis), 这个约束条件, 一般叫做原假设. 我们想用观测数据来判断原假设是否正确.

统计检验有一个基本概念叫做第Ⅰ类错误和第Ⅱ类错误. 如果原假设是正确的, 但我们错误地将它拒绝了, 这称为第Ⅰ类错误; 如果原假设是错误的, 但我们却错误地接受它, 这称为第Ⅱ类错误. 第Ⅰ类错误和第Ⅱ类错误都会导致关于假设检验的错误结论.

为什么第Ⅰ类错误和第Ⅱ类错误这么重要呢?在观测数据容量有限的情况下, 很难杜绝这两类错误. 统计检验的一个目标就是同时控制这两类错误, 即将这两类错误控制在一定水平之下.

防止第Ⅰ类错误为什么重要呢?比如说最近的新冠肺炎疫情, 如果一个人患有新冠肺炎, 但是核酸试剂检验却显示阴性, 这是假阴性, 是第Ⅰ类误差. 假阴性的后果是什么?如果将这个人放到社会上, 就可能会感染很多人. 另一种可能的检验结果是假阳性, 一个人本来没有患新冠肺炎, 但是如果核酸试剂因质量或其他问题检验结果为阳性, 那就要对这个人隔离治疗, 并追溯其密切接触者, 可能还要关闭其所在社区, 这种假阳性(第Ⅱ类错误)也会造成很高的社会成本.

假设检验的一个重要应用是产品质量控制. 现代制造业大都是自动化流水线作业, 不可能逐个去检查产品是否合格, 一般是通过抽样获得一个随机样本, 然后利用这个随机样本检查产品质量. 如果检验结果发现次品率不高于一个给定的临界值, 那就意味着产品在允许范围内是合格的. 这其实是假设检验的基本思想. 这种方法, 在20世纪50年代的日本和20世纪70年代的美国的制造业产品质量控制中, 发挥了非常重要的作用. 这种假设检验的基本思想也可应用于中国制造业改进产品质量.

与假设检验相关的另一个重要基本概念是$ P $值. 什么是$ P $值呢?比如说要检验一个参数是否为0, 我们通过一定的统计方法得到了一个参数估计值, 现在要判断这个参数估计值是否接近0. 如果接近0, 我们就接受原假设; 如果参数估计值显著地偏离0, 那原假设就是错误的. 我们可以构造一个$ t $检验统计量, 定义为参数估计值除以它的标准误估计. 在原假设成立的条件下, 它服从一个学生$ t $-分布或者在大样本条件下趋于标准正态分布. 我们可以从学生$ t $-分布或标准正态分布得到一个临界值, 如果$ t $检验统计量的绝对值大于这个临界值, 那我们在一定显著水平上拒绝原假设; 反之, 就在同样的显著水平上接受原假设. 这个显著水平就是第Ⅰ类错误的概率. 我们也可以用$ P $值作为一种等价的检验方法, 所谓$ P $值是在原假设成立的条件下观测到基于观测数据的$ t $-检验统计量的实现值的概率. 如果基于观测数据的$ t $检验统计量的实现值很大, 那么相应的$ P $值就很小, 我们可以在一定的显著水平上拒绝原假设. $ P $值越小, 我们越有数据证据拒绝原假设. 但是需要强调, 这种拒绝只是一种统计显著性.

什么是统计显著性呢?如果真实参数值不等于0, 但非常接近0, 因此只要增加样本容量, $ P $值会越变越小, 最终在一定的显著性水平上拒绝原假设. 但这种统计显著性并不意味着参数值偏离0的幅度很大, 特别是样本容量很大时, $ P $值会变得很小, 但参数值偏离0的幅度本来也可能很小, 以至其经济重要性可以忽略不计. 因此统计显著性和经济重要性是两回事. 只要样本容量足够大, 一个经济上并不重要的微小差别也可能显示出统计显著性. 这种情形, 在大数据时代, 更有可能发生.

另一方面, 如果$ P $值很大, 不存在统计显著性, 不能拒绝参数值为0的原假设, 这是否意味着参数值不具有经济重要性?首先, 即使真实参数值很大, 如果样本容量太小, 参数估计量的方差会很大, 因此相应的$ P $值也很大, 数据没有显示出足够强的证据拒绝原假设. 另外, 假设统计模型是一个线性回归模型, 在这种情形下, 接受参数值为0的原假设, 并不意味着相关的经济变量不重要, 因为真实的经济关系有可能是非线性关系.

由于上述及其他原因, 美国统计学会呼吁慎用$ P $值(Wasserstein & Lazar (2016)). 当然, 这并不是说放弃使用$ P $值.

当用一个统计模型解释观测数据时, 常常会使用拟合优度(goodness of fit)来测度模型的表现, 比如一个线性回归模型的拟合优度一般用所谓的$ R^2 $测度, $ R^2 $越高表示线性模型能够解释因变量变化的程度也就越大. 但是$ R^2 $高, 并不意味着线性回归模型是正确设定, 反之$ R^2 $低, 也不一定是模型误设. 在所谓的"伪回归"模型中(Granger & Newbold (1974)), 解释变量和因变量是互相独立的随机游走过程(因此是非平稳时间序列), 但其$ R^2 $接近1.

什么是正确模型设定呢?假设我们对一个条件均值$ E(Y|X) $建模, 其中因变量$ Y $代表消费, 解释变量$ X $代表收入, 这个条件均值是一个消费函数, 即给定收入水平, 预期的消费能达到多高. 对这个条件均值取一阶导数, 便得到所谓的边际消费倾向(marginal propensity to consume, MPC), 即收入每增加1元, 预期的消费能增加多少. 消费函数是凯恩斯经济学"乘数效应" (multiplier effects)的核心概念, 各种货币政策与财政政策的乘数效应的大小取决于边际消费倾向的高低. 很明显, 如果消费函数是收入的线性函数, 那么边际消费倾向是一个常数; 如果消费函数是一个非线性函数, 如收入的二次项函数, 则边际消费倾向就不是常数, 而会随着收入的变化而变化. 如果条件均值即真实消费函数是一个线性函数, 我们说线性模型是消费函数的正确设定. 反之, 如果真实消费函数是一个非线性(如二次项)函数, 那么线性模型是一个误设模型, 其解释变量收入的系数并不等于真实的边际消费倾向. 可以看出, 模型的正确设定是赋予模型参数正确经济解释的一个前提条件.

模型误设可能会导致其他严重的后果. 在数字经济时代, 很多经济交易特别是金融交易与银行业务, 都是基于统计模型或机器学习, 比如说算法交易、量化投资等. 模型误设会导致什么后果呢?可能会产生很大的金融衍生产品定价误差, 过高或者过低地估计某个金融产品的价格, 或者在风险管理导致严重的后果, 比如信用风险模型低估了小微企业的信用风险, 从而出现很高的贷款不良率. 这种因为模型误设可能带来的严重后果, 称为模型风险(model risk). 金融学有一个专门领域在研究模型风险(参见Morini (2011)).

导致模型风险的原因很多, 模型误设是一个主要原因. 另外一个原因是经济出现结构性的变化, 即经济结构具有时变性. 模型可能以前预测得不错, 但是在结构发生变化的条件下, 原有模型, 包括模型参数或模型的函数形式没有更新, 也会导致模型误设. 还有另外一种情形, 模型在正常的市场波动条件下表现不错, 但是在极端的市场波动条件下, 就不再适用. 比如20世纪90年代, 长期资本投资公司在俄罗斯的投资遭遇很大的损失, 就是因为他们所用的信用风险模型无法在极端的市场波动条件下准确地估计信用风险. 2007年的美国次贷危机, 基于流行的高斯连接模型(Gaussian copula model)也未能很好地刻画极端市场波动条件下市场之间的关联.

随着大数据时代的到来, 机器学习已经成为现代统计学的一个重要方法与工具. 所谓机器学习, 就是利用计算机算法程序自动分析大数据, 基于现有数据或训练数据进行样本外预测(包括分类预测). 机器学习预测就是通过一定的算法预测未知的数据或数据类型. 在理论上, 预测可表示为一个数学优化问题, 而这个数学优化问题可通过设计计算机算法程序来自动实施. 为了获得精准的样本外预测, 一般将数据分成至少两个部分, 一个部分是训练数据(training data), 另外一部分是检验数据(test data). 训练数据用来训练计算机算法程序, 挖掘训练数据中系统性的变量特征与变量之间的统计关系, 比如说相关性, 然后用以预测未知数据. 为了得到较好的样本外预测, 必须防止训练数据过度拟合(overfitting). 所谓过度拟合是指从训练数据中过度挖掘变量特征与变量之间的统计关系, 这些统计关系有一些在未知数据中会重复出现, 但另外一些关系只会在训练数据中出现, 在未知数据中并不会再次出现. 防止过度拟合就是要防止挖掘只会出现在训练数据中的关系, 并用以预测未知数据. 为了防止这种可能性, 一般是将经过训练的算法应用于检验数据, 同时引进一个惩罚项, 惩罚对训练数据的过度拟合. 因此机器学习本质上是一个数学优化问题, 目的是为了达到样本外的最佳预测, 实现方式是一个计算机算法程序. 一般情况下, 机器学习一般并不假设一个统计参数模型(如线性回归模型), 因此具有灵活的数据拟合能力, 在某种意义上, 机器学习本质上更接近非参数建模, 如决策树(decision tree)、随机森林(random forest)、$ k $近邻算法($ k $-nearest neighbors, KNN)、人工神经网络(artificial neutral network, ANN)与深度学习(deep learning)等, 参见Biau, Devroye & Lugosi (2008), Breiman (2001), Scornet, Biau & Vert (2015), White (1992)等.

在实际应用中, 多数情况下机器学习预测是比较准确的, 而这种预测并不是根据经济因果关系, 而是通过挖掘数据中的变量特征与变量之间的统计关系, 比如说相关性或预测关系, 通过这些统计关系来实现精准预测.

那么, 在大数据时代, 是不是只要相关性, 不需要因果关系了?其实不是. 经济学研究的最主要目的还是为了挖掘经济变量之间的因果关系, 从而揭示经济运行规律. 一个经济理论有没有真正的解释力, 必须基于可验证的因果关系, 单凭预测关系、相关关系并不具有理论解释力. 那么机器学习是否能够帮助我们识别与测度经济因果关系呢?所谓因果关系, 是指在其他变量$ Z $不变的条件下, 通过改变解释变量$ X $, 观测结果变量$ Y $是否随之改变. 在实验科学中, 通过可控实验可以控制其他因素$ Z $不变, 只让解释变量$ X $变化, 然后观测结果变量$ Y $是否变化. 实验方法因此是测度从$ X $到$ Y $的因果关系的最好方法. 但是在经济学与社会科学中, 一般情况下做不到可控实验, 经济数据大都是观测数据, 我们观测到的结果变量$ Y $, 是由政策变量$ X $以及其他因素$ Z $共同作用的结果. 我们没有办法控制其他因素$ Z $不变, 只能控制政策变量$ X $的变化. 在这种情况下, 识别与测度经济变量之间的因果关系, 就存在更大的挑战性.

统计学的反事实估计方法(counterfactual estimation)可用来识别与测度经济因果关系(参见Pearl (2009); Varian (2016)). 在现实经济中, 实施一个政策$ X $时, 其他变量$ Z $也在变化, 我们观测到的因变量$ Y $是政策$ X $以及其他变量$ Z $共同作用的结果. 所谓的反事实, 是指假设政策$ X $没有实施, 而其他不可控因素$ Z $继续变化, 此时因变量的结果$ Y^{\ast} $称为反事实. 在政策已实施的现实条件下, 假设政策没有实施, 这本身是一种虚拟假设, 这种情况下因变量的结果$ Y^{\ast} $是观测不到的, 所以叫做反事实. 反事实$ Y^{\ast} $可以通过机器学习精准地估计, 这种估计本质上是一种样本外预测. 样本外预测不一定是未来时间上的样本外, 也可以是另外一个未知的样本. 在这里, 机器学习之所以能够精准估计反事实$ Y^{\ast} $, 是通过挖掘大数据的相关性或者预测关系, 而不是通过经济因果关系, 但这种精准预测有助于我们识别经济政策$ X $对因变量$ Y $的因果关系, 并测度政策效应$ Y-Y^{\ast} $. 因此, 机器学习预测和测度经济因果关系, 两者并不矛盾.

这篇文章对概率论与统计学一些最基本的概念、思想、方法与工具所包含的经济含义, 以及它们在经济学的一些重要应用, 做了详细的阐述. 本文的一个主要目的是想说明, 在经济学研究越来越多使用定量方法的时候, 需要注意定量方法的可解释性特别是其经济可解释性, 同时理解定量分析方法如何应用于经济分析之中.

本文所讨论的例子没有也不可能覆盖所有概率论与统计学可以应用的范围. 我们希望本文能够通过抛砖引玉, 让大家多关注概率论与统计学在经济学应用的实例, 更加丰富这些实例. 通过这种方式, 使经济管理类的学生认识到学习经济数学特别是概率论与统计学的重要性, 同时更深刻理解概率论与统计学的经济含义及其在经济学的应用.

另一方面, 本文只是讨论概率论与统计学中一些基本的概念、思想、方法与工具在经济学的应用. 还有很多比较高深的概率论与统计学方法与工具, 本文没有讨论到, 但是它们在经济学中也有重要的应用. 例如, 在时间序列分析中, 任何平稳时间序列可以被分解为互相正交的不同频率的周期函数之和, 每个频率的权重大小可由谱密度函数(spectral density function)来刻画(参见Hong (2020)). 因此, 如果谱函数在某个频率出现一个峰值, 那就意味着该频率的随机权重最大, 因而主导着平稳时间序列的周期性动态变化. 若应用于宏观经济时间序列数据, 谱密度函数可以分析和刻画经济波动与经济周期(如Hamilton (1994) Chapter 6). 另一个例子, 常见的概率论与统计学主要关注随机变量或随机向量的概率法则, 没有涵盖随机集(random sets)的概率法则. 所谓随机集, 是指取值为一个集合的随机变量. 最简单的随机集例子是一维随机集, 即区间随机变量(interval-valued random variable), 其取值不是一个点, 而是一个区间. 常见例子包括每天的最低温和最高温、每个交易日的最低股价和最高股价、每天的低血压和高血压、每笔交易的买卖价格(bid-ask prices)等分别组成的区间数据. 与点数据相比, 区间数据包含更多信息, 但是区间数据长期没有得到有效利用. 区间数据建模具有很大的挑战性, 需要用到随机集概率论(参见Li, Ogura & Kreinovich (2002)), 甚至需要定义区间运算法则与两个区间随机变量的协方差, 需要建立区间随机变量的大数定律和中心极限定理等. Han, Hong & Wang (2018), Han et al. (2016)和Sun et al. (2018)率先提出了时间序列自回归区间模型, 在一个统一的分析框架中建立了模型、估计、检验的统计理论与方法. 区间数据建模在经济学有很广泛的应用空间, 包括宏观经济区间管理(参见孙玉莹、洪永淼和汪寿阳(2020)). 这些以及其他比较高深的概率论与统计学在经济学的应用, 将在后续研究中给予阐明.