量化估计一项政策干预的因果效应是许多经济学实证研究的基本目标.围绕这一目标, 已有文献主要在各种假设下考虑了总体的平均处理效应(average treatment effect, ATE)或仅针对处理组的平均处理效应(average treatment effect on the treated, ATT)的识别与估计.这方面比较有影响的综述文献包括: Angrist andKrueger (1999), Heckman, Lalonde and Smith (1999), Blundell and Dias (2002)等.在最近的综述文献中, Imbens (2004), Imbens and Wooldridge (2009)对处理效应这一研究主题的最新进展作了较全面的回顾.

虽然平均处理效应在衡量政策干预的因果效应方面非常重要, 但它并不能反映政策干预对目标变量分布影响的全貌.比如当施行一项政策后, 均值处理效应并不能衡量结果变量分布的方差是否发生了改变, 均值处理效应也不能反映政策干预对目标变量分布的影响, 包括在不同分位点的异质性影响.事实上, 有关目标变量分布方面的信息在许多应用中是非常重要的, 尤其在政策制定方面.例如, Freeman (1980), Card (1996)研究工会对工资差距的影响, Lalonde (1995), Abadie, Angrist and Imbens (2002)考虑政府培训项目对处于不同收入分布位置人群的影响, 以及政府补贴储蓄计划对处于储蓄分布低分位数人群的影响等.从政策制定的角度来说, 即使两项处理的平均处理效应是相同的, 政府更青睐有助于改善低收入群体处境的政策选择.为了刻画政策干预对目标变量的分布效应, Lehmann (1975), Doksum (1974)引入的分位数处理效应(quantile treatment effect, QTE)可作为一种直观且有效的工具.有关分位数处理效应的最新研究包括:Abadie et al. (2002), Chernozhukov and Hansen (2005), Donald and Hsu (2014), Firpo (2007), Frölich and Melly (2013)等.

政策评估文献中存在的另一个挑战是如何刻画Heckman and Robb (1985), Heckman, Smith and Clements (1997)所提到的处理变量对具有不同特征个体的异质效应.由于处理对不同个体的效应存在异质性, 因此研究者除了关心处理变量对整个总体的效应之外, 有时也关心政策对具有特定特征的子群体的效应.例如, 当估计母亲在怀孕期间吸烟对婴儿出生体重的影响时, 研究者感兴趣的可能是不同年龄段母亲吸烟对婴儿出生体重的异质效应.为此, Abrevaya, Hsu and Lieli (2015), Lee, Okui and Whang (2017)使用部分条件平均处理效应(partially conditional average treatment effect, PCATE)来刻画处理变量对具有不同特征子群体的条件平均效应.

本文试图提出一种新的处理效应模型来刻画处理变量对具有不同特征的子群体沿着目标变量分布方向上的异质效应.为此, 在无混淆假设成立的框架下, 我们提出使用部分条件分位数处理效应(partially conditional quantile treatment effect, PCQTE)来刻画给定某一连续协变量$Z$时, 处理变量对目标变量分布的异质效应, 其中变量$Z$是所有协变量$X$的一个真子集.在仅给定协变量$Z$的情况下, 无混淆假设一般不再成立.因此为了识别PCQTE, 我们需要新的方法与技巧.我们证明, 上述PCQTE是可非参数识别的, 并且提出一种新的半参数估计方法.此外, 在常见的正则条件下, 我们证明了提出的半参数估计是一致的且具有渐近正态性, 从而研究者可对PCQTE作为$Z$的函数做逐点统计推断.

我们的研究动机来自于如下健康经济学中的实际问题, 即考察不同年龄段母亲在首次怀孕时, 怀孕期间吸烟对婴儿出生体重的分布效应.在最近的文献中, Abrevaya et al. (2015), Lee et al. (2017)考虑了在给定母亲不同年龄下怀孕期间吸烟对婴儿出生体重的平均处理效应, 其中Abrevaya et al. (2015)提出了一种非参数和半参数方法估计给定连续协变量下的条件平均处理效应.为了避免非参数估计中的维数灾难问题, Lee et al. (2017)则基于参数回归模型提出了一种双稳健方法估计给定连续协变量下的条件平均处理效应.然而, 以上两篇文献都没有考虑在给定母亲年龄下, 母亲在怀孕期间吸烟对婴儿出生体重的异质分布效应.事实上, 我们的研究发现, 不管对白人还是黑人来说, 婴儿出生体重的分布都是非对称且厚尾的.因此, 本文提出的方法可能更适合分析这一实际数据.同时, 我们也将考察在母亲不同年龄下, 接受处理群体中的母亲在怀孕期间吸烟对婴儿出生体重的分位数处理效应, 即处理组下的部分条件分位数处理效应(partially conditional quantile treatment effect on the treated, PCQTT).总的来说, 我们的实证结果表明在不同母亲年龄组之间分位数处理效应存在实质性的差异, 在所有怀孕母亲年龄段中以及在所有分位数水平下, 母亲吸烟对婴儿出生体重均会产生显著的负效应.但是, 我们也发现, 当母亲年龄较大时, 母亲吸烟对婴儿出生体重的分位数效应会变得更强.对于白人母亲群体而言, 在给定母亲年龄的情况下, 部分条件分位数处理效应在低分位数水平的数值要大于其在中位数或较高分位数水平的数值, 而在黑人母亲群体中这一现象则不显著.

本文余下部分的具体安排如下: 第二部分介绍部分条件分位数处理效应(PCQTE和PCQTT)模型并讨论它们的识别条件以及估计方法, 并进一步给出估计量的渐近性质; 第三部分使用蒙特卡罗模拟来考察相应估计量的有限样本性质; 第四部分实证研究母亲在怀孕期间吸烟对婴儿出生体重的分位数处理效应如何在母亲的不同年龄组之间变化; 第五部分则是结论.附录包含了所有的理论证明.

假定$D_{i}$表示个体$i$的二元处理变量, 其中$D_{i}=1$表示个体$i$接受政策干预而$D_{i}=0$则表示未接受干预.使用Rubin (1974)中的潜在结果框架, 我们用$Y_{i}(0)$和$Y_{i}(1)$分别表示个体$i$未接受和接受处理时的潜在结果变量.注意到对每个个体来说, 我们只能观测到$Y_{i}(D_{i})$, 而$Y_{i}(1-D_{i})$是缺失的.因此, 观测结果变量$Y_{i}$与潜在结果变量$Y_{i}(0)$和$Y_{i}(1)$之间的关系可表示为:

$Y_{i}=(1-D_{i})\cdot Y_{i}(0)+D_{i}\cdot Y_{i}(1).$

此外, 我们用$X_{i}$表示每个个体可观测到的$L$维控制变量向量.在下文中, 我们假定$\big(Y_i(0), Y_i(1), X_i, D_i\big)$, $i=1, \cdots, n$是独立同分布的随机向量.对每个个体$i$来说, 我们只能观测到$Y_{i}(0)$和$Y_{i}(1)$中的一个, 因此为了识别感兴趣的处理效应参数, 我们需要如下假设:

假设 1  (i) (无混淆处理分配) 给定协变量$X_i$, 潜在结果$(Y_i(0), Y_i(1))$与处理变量$D_{i}$独立, 即:

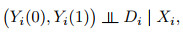
其中表示统计独立.

(ii) (共同支撑集) 对$X_{i}$支撑集中的任意取值$x$,

$ 0＜\underline{p}\leq p(x)=P(D_i=1|X_i=x)\leq\overline{p}＜1, $

其中$0＜\underline{p}＜\overline{p}＜1$, $p(x)$是倾向得分函数.

在统计学或计量经济学文献中, 假设1 (i)通常也称为"条件无混淆假设"条件独立性假设"或者"基于可观测选择假设"等, 相关文献可参见Rosenbaum and Rubin (1983), Lechner (1999, 2002).这一假设排除了那些不可观测的因素同时影响干预选择和潜在结果变量的情况.假设1 (ii)表明在整个总体中对于几乎所有的$X_{i}$的取值, 个体都有正的概率接受或者不接受处理.然而, 在实际应用中缺乏共同支撑是可能存在问题.解决这一问题的通常做法是去掉那些倾向得分值接近0或者1的个体, 从而只关注那些倾向得分值远离0和1的子集的处理效应.以上两个假设在处理效应文献中已被广泛使用, 如Heckman, Ichimura and Smith et al. (1998), Dehejia and Wahba (1999), Hirano, Imbens and Ridder (2003), Firpo (2007)等.

本文感兴趣的是在给定观测协变量$X_{i}$的一个子向量的条件下, 处理变量对结果变量的分位数处理效应, 我们称之为部分条件分位数处理效应(PCQTE).具体而言, 假设$Z_i$表示$X_i$的一个$k$维子向量, 其中$1\leq k\ll L$, 那么我们感兴趣的部分条件分位数处理效应定义为:

(1) ${\Delta _\tau }(z) = {q_{1, \tau }}(z) - {q_{0, \tau }}(z), $

其中$\tau\in(0, 1)$是分位数水平, $q_{j, \tau}(z)$是在给定$Z_i=z$下$Y_i(j)$的条件分位数函数, $j=0$或$1$.这里我们需要注意的是当研究者只控制$Z_i$而不是$X_i$时, 上面的条件无混淆假设不再成立.与此同时, 注意到如果在(\ref{eq1})中取$Z_i$为空集, 那么此时上面定义的部分条件分位数处理效应变为Firpo (2007)中考虑的无条件分位数处理效应.

因为我们无法同时观测到每个个体的潜在结果变量$Y_{i}(0)$和$Y_{i}(1)$, 因此$Y_1(j), \cdots, Y_n(j)$不可直接用来估计(1) 中的$q_{j, \tau}(z), j=0, 1$.现在我们定义$W_0(X_i, D_i)=(1-D_i)/[1-p(X_i)]$和$W_1(X_i, D_i)=D_i/p(X_i)$, 那么对于$j=0$和$1$以及具有有限数学期望的任意函数$g(\cdot)$, 在假设1下我们容易得到:

$E[{W_j}({X_i}, {D_i}){\mkern 1mu} g({Y_i})|{Z_i}] = E[{W_j}({X_i}, {D_i}){\mkern 1mu} g({Y_i}(j))|{Z_i}] = E[g({Y_i}(j))|{Z_i}], $

因而$q_{j, \tau}(z)$可被表示为:

(2) ${q_{j, \tau }}(z) = \arg {\min _q}E({\rho _\tau }({Y_i}(j);q)|{Z_i} = z) = \arg {\min _q}E({W_j}({X_i}, {D_i}){\rho _\tau }({Y_i};q)|{Z_i} = z), $

其中$\rho_{\tau}(Y; q)=(Y-q)\{\tau-I(Y\le q)\}$是Koenker and Bassett (1978), Koenker (2005)中考虑的分位数损失函数, $I\{\cdot\}$是示性函数.当倾向得分函数$p(x)$已知时, 根据Koenker and Bassett (1978), Koenker (2005)中的方法, 我们可对观测值$(Y_i, X_i, D_i)$, $i=1, \cdots, n$拟合一个加权分位数回归模型从而得到$q_{j, \tau}(z), j=0, 1$的估计.

由于在实际应用中$p(x)$一般是未知的, 因此根据(2)中的识别结果我们需要分两步来估计PCQTE参数$\Delta_{\tau}(z)$.首先, 我们使用数据$(X_i, D_i)$, $i=1, \cdots, n$获得倾向得分函数$p(x)$的估计, 记为$\widehat{p}_n(x)$; 其次, 在第二步中, 我们使用基于核函数的局部平均方法估计$q_{j, \tau}(z), j=0, 1$, 从而可进一步得到$\Delta_{\tau}(z)$的估计.具体地, 我们提出的$\Delta_{\tau}(z)$的估计为:

(3) ${\hat \Delta _\tau }(z) = {\hat q_{1, \tau }}(z) - {\hat q_{0, \tau }}(z), $

其中, 对于$j=0$和$1$,

(4) ${\hat q_{j, \tau }}(z) = \arg {\min _q}\frac{1}{n}\sum\limits_{i = 1}^n {{K_h}} ({Z_i} - z){\hat W_{n, j}}({X_i}, {D_i}){\rho _\tau }({Y_i};q), $

这里$\widehat{W}_{n, 0}(X_i, D_i)=(1-D_i)/[1-\widehat{p}_n(X_i)]$, $ \widehat{W}_{n, 1}(X_i, D_i)=D_i/\widehat{p}_n(X_i)$, $K_{h}(u)=K(u/h)/h$, $K(\cdot)$是一个核函数, $h$是窗框参数, $\widehat p_n(x)$是$p(x)$的一致估计.当然, 上面(4)中给出的估计方法可被推广到如下的局部线性估计方法:

$(\hat q_{j,\tau }^{ll}(z),\hat q_{j,\tau }^{'ll}(z)) = \arg {\min _{{q_0}, {\kern 1pt} {q_1}}}\frac{1}{n}\sum\limits_{i = 1}^n {{K_h}} ({Z_i} - z){\hat W_{n, j}}({X_i}, {D_i}){\rho _\tau }({Y_i};{q_0} + {q_1}({Z_i} - z)), {\mkern 1mu} j = 0, 1, $

进而可得到$\Delta_{\tau}(z)$的局部线性估计$\widehat\Delta_{\tau, ll}(z)=\widehat{q}^{ll}_{1, \tau}(z)-\widehat{q}^{ll}_{0, \tau}(z)$.估计$\widehat\Delta_{\tau, ll}(z)$的理论性质的推导应与$\widehat\Delta_{\tau}(z)$类似, 因此为了简单起见, 在下文中我们只给出$\widehat\Delta_{\tau}(z)$的渐近理论性质.

接下来的问题是如何获得$p(x)$的一致估计.在已有文献中存在两种常用的方法可用来估计$p(x)$.第一种方法是参数方法, 即为$p(x)$设定一个参数模型$p(x)=p(x;\theta)$, 如logit或者probit模型, 然后使用极大似然方法估计模型中的未知参数.第二种方法是非参数方法, 其包括Hirano et al. (2003), Firpo (2007)中使用的级数逻辑估计(series logit estimator), Ichimura and Linton (2005)中使用的局部多项式回归估计以及Abrevaya et al. (2015)中使用的高阶核回归估计等.在本文中, 我们采用参数方法估计$p(x)$, 因此(3)中得到的估计称为半参数估计.当然, 我们也可在第一步中采用非参数方法估计$p(x)$, 这样便得到感兴趣参数$\Delta_{\tau}(z)$的非参数估计, 我们猜测在一些正则条件下$\Delta_{\tau}(z)$的非参数估计具有与下文中理论结果相似的性质.

在这一部分, 我们研究(3) 中提出的半参数估计$\widehat\Delta_{\tau}(z)$的渐近性质.虽然对任意的$k$ ($1\leq k＜L$) 维向量$Z_i$, 我们可得到$\widehat{\Delta}_{\tau}(z)$的渐近理论, 但为了简单起见, 这里我们只给出$k=1$时的结果.正如在Abrevaya et al. (2015)中所指出的, 实际应用中$k=1$是最常见的情形.此时估计结果$\widehat{\Delta}_{\tau}(z)$可在二维平面中展示出来.在研究提出估计方法的渐近性质之前, 我们需要下面的一些假设.

假设 2  ($X_i$和$Z_i$的分布) 存在一个常数$c>0$使得$X_i$的密度函数$f_X(x)$满足$\inf_{x\in\mathcal{X}}f_X(x)\geq c$, 其中$\mathcal{X}$表示$X_i$的支撑集.同时, $Z_i$的密度函数$f_Z(z)$在其支撑集上二阶连续可导.

假设 3  (i) 对于$j=0$和$1$, 条件密度函数$f_{Y(j)|X}(y|x)$在$Y_i(j)$和$X_i$的支撑集上连续且有界. (ii)条件密度函数$f_{Y(j)|Z}(y|z)$连续且在$q_{j, \tau}(z)$的某个邻域内一致有界并且远离0;此外, $f_{Y(j)|Z}(y|z)$关于$z$二阶可导, 关于$y$的导数在$Y_i(j)$和$Z_i$的支撑集内连续有界.

假设 4  (核函数和窗框) (i) 核函数$K(u)$是一个具有紧支撑集的对称密度函数, 且它在其支撑集上连续可导. (ii)对某一$\varepsilon>0$, 当$n\rightarrow \infty$时, $h\rightarrow0$, $nh^{1+\varepsilon}\rightarrow\infty$且$nh^{5}$有界.

假设 5  (参数倾向得分函数) 假设倾向得分函数具有参数形式$p(x)=p(x;\theta_{0})$, 其中$\theta_0$是具有固定维数的参数.进一步我们假设估计得到倾向得分函数$\widehat{p}_n(x)=p(x;\widehat{\theta}_{n})$满足$\sup_{x\in\mathcal{X}}\big|p(x;\widehat{\theta}_{n})-p(x;\theta_{0})\big|=O_{p}(n^{-1/2})$.

假设2中关于$X_{i}$分布的约束在处理效应文献中经常被使用, 如Hirano et al. (2003), Abadie and Imbens (2006, 2016), Firpo (2007), Abrevaya et al. (2015)等.假设3保证(2) 中的解是唯一的, 而施加的光滑性条件在实际应用中容易得到满足.假设4中关于核函数和窗框的条件在非参数估计文献中经常被使用.许多常用的核函数, 如Epanechnikov核函数等均满足这一要求.在某些正则条件下, 对于标准的参数估计方法, 假设5都是成立的.

接下来我们在下面的定理中给出估计$\widehat\Delta_\tau(z)$的渐近性质, 其证明见后面的附录.为符号表示简单起见, 我们先定义一些符号.对于$j=0$和$1$, 定义$F_j(y|z)=F_{Y(j)|Z}(y|z)$为$Y(j)$在给定$Z=z$下的条件分布函数, 其关于$z$的$m$阶导数记为$F_j^{(m)}(y|z)=\partial^m F_j(y|z)/\partial z^m$.对于$j=0$和$1$, 记$\psi_{j}(Y_i, X_i, D_i; z)=W_j(X_i, D_i)(I\{Y_i\leqq_{j, \tau}(z)\}-\tau)$和$\delta_\tau(z)=\delta_{1, \tau}(z)-\delta_{0, \tau}(z)$, 其中,

(5) ${\delta _{j, \tau }}(z) = \frac{{2{f_{Z'}}(z)F_j^{(1)}({q_{j, \tau }}(z)|z)}}{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}} + \frac{{F_j^{(2)}({q_{j, \tau }}(z)|z)}}{{{f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}.$

定理 1  在假设1$\sim$5下, 对于$Z_i$支撑集中的任意一点$z$, 我们有:

(6) $\begin{array}{l}\sqrt {nh} \left[ {{{\hat \Delta }_\tau }(z) - {\Delta _\tau }(z) + \frac{{{h^2}}}{2}{\mu _2}(K){\delta _\tau }(z) + {o_p}({h^2})} \right] = \\ - \frac{1}{{\sqrt {nh} }}\frac{1}{{{f_Z}(z)}}\sum\limits_{i = 1}^n \{ \frac{{h{K_h}({Z_i} - z){\psi _1}({Y_i}, {X_i}, {D_i}, z) - E(h{K_h}({Z_i} - z){\psi _1}({Y_i}, {X_i}, {D_i}, z))}}{{{f_{Y(1)|Z}}({q_{1, \tau }}(z)|z)}} - \\\frac{{h{K_h}({Z_i} - z){\psi _0}({Y_i}, {X_i}, {D_i}, z) - E(h{K_h}({Z_i} - z){\psi _0}({Y_i}, {X_i}, {D_i}, z))}}{{{f_{Y(0)|Z}}({q_{0, \tau }}(z)|z)}}\} + {o_p}(1)\end{array}$

(7) $\mathop \to \limits^D {\cal N}(0, {\nu _0}(K)\sigma _\tau ^2(z)/{f_Z}(z)), $

其中$\delta_\tau(z)$在(5) 中定义, $\mu_{2}(K)=\int u^{2}K(u){\rm d}u$, $\nu_0(K)=\int K^{2}(u){\rm d}u$,

$\sigma _\tau ^2(z) = E\{ {(\frac{{{\psi _1}({Y_i}, {X_i}, {D_i}, z)}}{{{f_{Y(1)|Z}}({q_{1, \tau }}(z)|z)}} - \frac{{{\psi _0}({Y_i}, {X_i}, {D_i}, z)}}{{{f_{Y(0)|Z}}({q_{0, \tau }}(z)|z)}})^2}|{Z_i} = z\} .$

根据定理1, 我们可知(6) 中的第一项是半参数估计$\widehat\Delta_\tau(z)$的一阶近似, 即所谓的局部Bahadur表达式, 参见Cai and Xu (2008).一阶近似使得(7)中的渐近分析更为容易.根据上面定理1中的理论结果, 对每个给定的$z$, 为了构造$\Delta_{\tau}(z)$的置信区间, 在忽略渐近偏差项的情况下, 我们仍然需要获得$f_Z(z)$和$\sigma^{2}_{\tau}(z)$的一致估计.显然, $Z_i$的密度函数的一致估计可由核密度估计$\widehat{f}_Z(z)=\frac{1}{n}\sum_{i=1}^{n}K_h(Z_{i}-z)$得到.然而, 这里更具挑战的是一致性地估计$\sigma^{2}_{\tau}(z)$, 因为它涉及未知的条件密度函数$f_{Y(j)|Z}(q_{j, \tau}(z)|z), j=0, 1$.正如在Koenker and Xiao (2004), Koenker (2005), Cai and Xu (2008)中所指出的, 获得条件密度函数$f_{Y(j)|Z}(q_{j, \tau}(z)|z)$的一致估计并非易事.对于$j=0$和$1$, 我们根据Koenker (2005)中的方法提出以下方法估计未知条件密度函数$f_{Y(j)|Z}(q_{j, \tau}(z)|z)$, 即,

${\hat f_{Y(j)|Z}}({q_{j, \tau }}(z)|z) = \frac{{2{h^*}}}{{{{\hat q}_{j, \tau + {h^*}}}(z) - {{\hat q}_{j, \tau - {h^*}}}(z)}}, $

其中$h^*$是一个窗框参数.事实上, 在$h^*\rightarrow0$且$h^*\sqrt{nh}\rightarrow\infty$的条件下, Koenker (2005)证明了$\widehat{f}_{Y(j)|Z}(q_{j, \tau}(z)|z)\stackrel{p}{\longrightarrow}f_{Y(j)|Z}(q_{j, \tau}(z)|z)$.由此我们可得到$\sigma^{2}_{\tau}(z)$的一致估计为:

$\hat \sigma _\tau ^2(z) = \sum\limits_{i = 1}^n {{K_h}} ({Z_i} - z){(\frac{{{{\hat \psi }_1}({Y_i}, {X_i}, {D_i};z)}}{{{{\hat f}_{Y(1)|Z}}({q_{1, \tau }}(z)|z)}} - \frac{{{{\hat \psi }_0}({Y_i}, {X_i}, {D_i};z)}}{{{{\hat f}_{Y(0)|Z}}({q_{0, \tau }}(z)|z)}})^2}/\sum\limits_{i = 1}^n {{K_h}} ({Z_i} - z), $

其中对于$j=0$和$1$, $\widehat{\psi}_j(Y_{i}, X_{i}, D_{i};z)=\widehat{W}_{n, j}(X_i, D_i)\big(I\{Y_{i}\leq\widehat{q}_{j, \tau}(z)\}-\tau\big)$.最后, 通过忽略渐近偏差项, 我们可计算$\Delta_\tau(z)$的逐点置信区间.

一般来说, 政策制定者除了对整个总体的处理效应感兴趣之外, 还可能对处理组这一群体的处理效应感兴趣, 相关文献可参见Heckman and Robb (1985), Heckman et al. (1999).当然, 在处理组这一群体中, 处理变量对每个个体的处理效应也可能是异质的.因此, 我们在这一部分考虑处理组的部分条件分位数处理效应(partially conditional quantile treatment effect on the treated, PCQTT), 其定义为:

${\Delta _{\tau |D = 1}}(z) = {q_{1, \tau |D = 1}}(z) - {q_{0, \tau |D = 1}}(z), $

其中$q_{j, \tau|D=1}(z)=\inf\big\{y:P(Y_i(j)\leq y\mid Z_i=z, D_i=1)\geq\tau\big\}$是$Y_i(j)$在给定$Z_i=z$和$D_i=1$的条件$\tau$分位数函数, $j=0$或$1$.

为了给出$\Delta_{\tau|D=1}(z)$的半参数估计, 我们先定义$V_1(X_i, D_i)=D_i$和$V_0(X_i, D_i)$$=(1-D_i)p(X_i)/\big[1-p(X_i)\big]$.于是, 根据迭代期望定律(law of iterated expectations)和条件无混淆假设, 对于任意具有有限数学期望的函数$g(\cdot)$, 则有:

$E({V_j}({X_i}, {D_i})g({Y_i})|{Z_i} = z) = E({V_j}({X_i}, {D_i})g({Y_i}(j))|{Z_i} = z) = E({D_i} \cdot g({Y_i}(j))|{Z_i} = z).$

因此, 类似于前面的(2) 式, 条件分位数函数$q_{j, \tau|D=1}(z)$可被识别为:

${q_{j, \tau |D = 1}}(z) = \arg {\min _q}E({V_j}({X_i}, {D_i}){\rho _\tau }({Y_i};q)|{Z_i} = z).$

由此, 我们可得到PCQTT参数$\Delta_{\tau|D=1}(z)$的半参数估计为:

${\hat \Delta _{\tau |D = 1}}(z) = {\hat q_{1, \tau |D = 1}}(z) - {\hat q_{0, \tau |D = 1}}(z), $

其中,

${\hat q_{j, \tau |D = 1}}(z) = \arg {\min _q}\frac{1}{n}\sum\limits_{i = 1}^n {{K_h}} ({Z_i} - z){\hat V_{n, j}}({X_i}, {D_i}){\rho _\tau }({Y_i};q), $

这里$\widehat{V}_{n, 0}(X_i, D_i)=(1-D_i)\widehat{p}_{n}(X_i)/\big(1-\widehat{p}_{n}(X_i)\big)$, $\widehat{V}_{n, 1}(X_i, D_i)=D_i$, $\widehat{p}_{n}(x)$是$p(x)$的参数估计.为了给出半参数估计$\widehat{\Delta}_{\tau|D=1}(z)$的大样本性质, 我们需要将前面的假设3稍加修改.

假设 3^*  (i) 对于$j=0$或$1$, 条件密度函数$f_{Y(j)|X, D=1}(y|x)$在$Y_i(j)$和$X_i$的支撑集上连续且有界.(ii) 条件密度函数$f_{Y(j)|Z, D=1}(y|z)$连续且在$q_{j, \tau|D=1}(z)$的某个邻域内一致有界并且远离0;$f_{Y(j)|Z, D=1}(y|z)$关于$z$二阶可导, 且它关于$y$的一阶导数在$Y_i(j)$和$Z_i$的支撑集内连续有界. (iii)$p_Z(z)=P(D_i=1|Z_i=z)$二阶连续可导.

为了符号表示简单起见, 我们记$\varphi_{1}(Y_{i}, X_{i}, D_{i};z)=V_1(X_i, D_i)\big(I\{Y_{i}\leqq_{1, \tau|D=1}-\tau\}\big)$和$\varphi_{0}(Y_{i}, X_{i}, D_{i};z)=V_0(X_i, D_i)\big(I\{Y_{i}\leqq_{1, \tau|D=1}-\tau\}\big)$.对于$j=0$或$1$, 定义$F_{j|D=1}(y|z)=F_{Y(j)|Z, D=1}(y|z)$为$Y(j)$在给定$Z=z$和$D=1$下的条件累积分布函数.对于$m\geq0$, $F_{j|D=1}(y|z)$关于$z$的$m$阶导数记为$F^{(m)}_{j|D=1}(y|z)=\partial^{m}F_{j|D=1}(y|z)/\partial z^{m}$.记$\zeta_{\tau}(z)=\zeta_{1, \tau|D=1}-\zeta_{0, \tau|D=1}$, 其中对于$j=0$或$1$,

$\begin{array}{l}{\zeta _{j, \tau |D = 1}} = \frac{1}{{{p_Z}(z){f_Z}(z){f_{Y(j)|Z, D = 1}}({q_{j, \tau |D = 1}}(z)|z)}}\{ 2{p_Z}(z){{f'}_Z}(z)F_{j|D = 1}^{(1)}({q_{j, \tau |D = 1}}(z)|z)\\\;\;\;\;\;\;\;\;\;\;\;\; + {p_Z}(z){f_Z}(z)F_{j|D = 1}^{(2)}({q_{j, \tau |D = 1}}(z)|z) + 2{{p'}_Z}(z){f_Z}(z)F_{j|D = 1}^{(1)}({q_{j, \tau |D = 1}}(z)|z)\} .\end{array}$

类似于定理1, 以下定理总结了半参数估计$\widehat{\Delta}_{\tau|D=1}$的渐近性质, 其证明类似于定理1, 故略去.

定理 2  在假设1, 2, 3^*, 4以及5下, 对于$Z_i$支撑集中的任意一点$z$, 我们有:

$\sqrt {nh} [{\hat \Delta _{\tau |D = 1}}(z) - {\Delta _{\tau |D = 1}}(z) + \frac{{{h^2}}}{2}{\mu _2}(K){\zeta _\tau }(z) + {o_p}({h^2})]\;\;\mathop \to \limits^D \;\;{\cal N}(0, \sigma _{\tau, T}^2), $

其中$\sigma_{\tau, T}^2=\nu_{0}(K)\sigma^{2}_{\tau|D=1}(z)/\big[p^{2}_{Z}(z)f_{Z}(z)\big]$,

(17) $\sigma _{\tau |D = 1}^2(z) = E\{ {(\frac{{{\varphi _1}({Y_i}, {X_i}, {D_i};z)}}{{{f_{Y(1)|Z, D = 1}}({q_{1, \tau |D = 1}}(z)|z)}} - \frac{{{\varphi _0}({Y_i}, {X_i}, {D_i};z)}}{{{f_{Y(0)|Z, D = 1}}({q_{0, \tau |D = 1}}(z)|z)}})^2}|{Z_i} = z\}, $

其它记号与定理1中具有相同的含义.

在这一部分, 我们使用蒙特卡罗模拟试验来考察前面提出估计方法的有限样本性质, 其目的是考察提出估计方法在各种情形下的有限样本表现.

例 1  我们考虑使用潜在结果变量$Y(0)$和$Y(1)$的Skorohod表示¹.具体地, 我们考虑的数据产生过程为:

$Y(0) = {\lambda _0}{X_1} + {\gamma _0}\sqrt {{U_0}} {X_2}\;\;和\;\;Y(1) = {\lambda _1}{X_1} + {\gamma _1}\sqrt {{U_1}} {X_2},$

¹有关Skorohod表示的定义, 读者可参见Durrett(1996).

其中$\lambda_0=3.0$, $\gamma_0=0.4$, $\lambda_1=4.0$, $\gamma_1=1.6$, $U_{0}$和$U_{1}$独立地从均匀分布$U[0, 1]$中产生, $X_1$和$X_2$相互独立且$X_{1}\sim U[0, 1]$和$X_{2}\sim\text{Beta}(3, 1)$, 倾向得分函数为:

$P(D = 1|{X_1}, {X_2}) = \frac{{\exp \{ - 0.5 + {X_1} + {X_2}\} }}{{1 + \exp \{ - 0.5 + {X_1} + {X_2}\} }}.$

此外, 条件变量$Z$取为$X_{1}$.在以上情形下, 对于$j=0$或$1$, 通过简单计算可得到$Y(j)$在给定$Z=z$下的条件分位数函数为:

(8) ${q_{j, \tau }}(z) = {\lambda _j}z + {\gamma _j}{a_\tau }, $

其中$a_\tau$是方程$-2a^3+3a^2-\tau=0$在区间$(0, 1)$上的唯一解.因此, 我们可得到PCQTE为:

(9) ${\Delta _\tau }(z) = ({\lambda _1} - {\lambda _0})z + ({\gamma _1} - {\gamma _0}){a_\tau }.$

为了考察估计$\widehat{\Delta}_{\tau}(z)$的有限样本表现, 我们使用如下的平均绝对偏差准则(mean absolute deviation error, MADE)

${\rm{MADE}}({\hat \Delta _\tau }(\cdot)) = \frac{1}{m}\sum\limits_{j = 1}^m | {\hat \Delta _\tau }({z_j}) - {\Delta _\tau }({z_j})|, $

其中$\{z_{j}\}_{j=1}^{m}$是取自$Z$的支撑集中的格点.为了计算(3) 中的半参数估计$\widehat{\Delta}_{\tau}(z)$, 这里我们使用Epanechnikov核函数$K(u)=0.75(1-u^2)I(|u|\le 1)$.众所周知, 在非参数核类型的估计中窗框的选择是一个重要的问题, 因此为了考察窗框$h$的选择如何影响估计$\widehat{\Delta}_{\tau}(z)$的表现, 根据前面的假设4, 这里我们设窗框参数$h$为$h=c\cdot n^{-1/5}$, 其中$c\in \{0.25, 0.5, 1.0\}$.在处理效应文献中, 通常需要对估计得到的倾向得分函数进行截断以防其太接近0或者1.因此, 根据文献中的通常做法, 我们在下面的模拟中也将估计得到的倾向得分函数$\widehat{p}_{n}(x)$进行截断使其位于$[0.005, 0.995]$之间.

为了计算MADE值的中位数与标准差, 对于考虑的每种情形我们重复蒙特卡罗模拟1000次.表 1报告了半参数估计的模拟结果.根据表 1中的结果, 我们可看见就MADE值而言, 我们所提出的半参数估计表现良好, 而根据MADE值及其标准差的表现, 窗框$h$似乎应该设为$h=0.5n^{-1/5}$.正如所预期的, 由于在尾部区域样本稀疏, 因此提出的估计在中位数区域比尾部区域表现要好.最后, 我们从表 1中可清楚地看见随着样本容量从$n=500$增加到$n=2000$时, MADE值及其标准差会显著减少, 这与前面得到的渐近理论是一致的.

例 2  我们在第二个实验中考察前文所提出的半参数估计量$\widehat{\Delta}_{\tau|D=1}(z)$的有限样本表现, 其数据产生过程与例1相同, 条件变量$Z$同样选择$X_{1}$, 模拟重复次数为1000次.表 2报告了半参数估计量$\widehat{\Delta}_{\tau|D=1}(z)$的模拟结果.

根据表 2中的模拟结果, 我们可观察到与例1中相似的模式.具体而言, 类似于半参数估计量$\widehat{\Delta}_{\tau}(z)$, 半参数估计量$\widehat{\Delta}_{\tau|D=1}(z)$也在有限样本中表现良好.此外, 窗框参数$h$在某一范围内的选择似乎对MADE值及其标准差的影响较小.我们从表 2中可再次观察到半参数估计量$\widehat{\Delta}_{\tau|D=1}(z)$在中位数区域的表现要比尾部区域好, 且当样本容量从$n=500$增加到$n=2000$时, MADE值及其标准差会显著减小.

许多研究表明婴儿出生体重偏低与其将来的健康、教育以及劳动力市场表现相关, 但研究者对这一影响的具体大小还存在争议, 这方面的文献可参看Abrevaya (2006), Almond, Chay and Lee (2005), Currie and Almond (2011)等.众所周知, 存在许多风险因素可引起婴儿出生体重偏低, 但一般认为母亲在怀孕期间吸烟是引起婴儿出生体重偏低的最重要因素, 有关这方面的更多讨论见Kramer (1987).在过去几十年里, 许多研究者试图使用各种方法估计母亲在怀孕期间吸烟对婴儿出生体重的效应.最近有研究者使用政策评估的方法估计这种效应, 相关文献如Almond et al. (2005), Abrevaya (2006), Da Veiga and Wilder (2008), Abrevaya and Dahl (2008), Abrevaya et al. (2015)等.本文感兴趣的是母亲在怀孕期间吸烟对初生婴儿体重的分布影响如何随母亲年龄而变化.为了刻画这种异质效应, 我们使用前面提出的方法估计在给定母亲不同年龄条件下, 母亲在怀孕期间吸烟对婴儿出生体重的分位数处理效应, 而不是Abrevaya et al. (2015), Lee et al.(2017)所考虑的不同年龄下母亲孕期吸烟对初生婴儿体重的条件平均效应.在本例中, 为了满足条件无混淆假设, 已有文献通常需要控制较多的协变量, 因此与Abrevaya et al. (2015), Lee et al.(2017)类似, 我们同样使用参数方法估计未知的倾向得分函数$p(x)$.

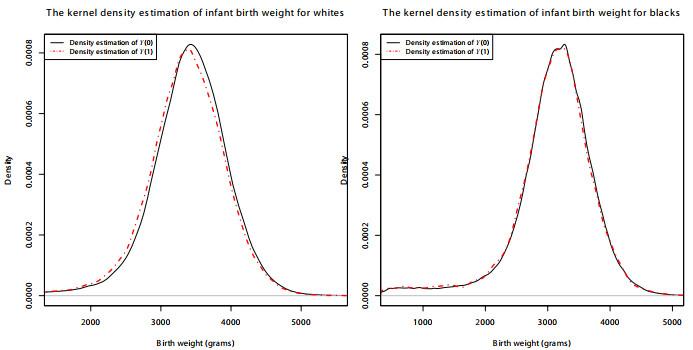
我们使用与Abrevaya et al. (2015)同样的数据集, 即由北卡罗来纳大学奥德姆研究所提供的1988年至2002年北卡罗来纳州健康服务中心的记录数据.我们的样本也仅使用初为人母的观察值, 并且根据文献中的通常做法, 将白人和黑人当作不同的样本处理, 其中白人样本的容量为433558, 而黑人样本的容量为157989.我们感兴趣的结果变量$Y$是婴儿的出生体重, 其度量用克表示, 而处理变量$D$是二元变量, 如果母亲在怀孕期间吸烟则$D=1$否则$D=0$. $Y(0)$表示母亲孕期未吸烟组婴儿的出生体重, 而$Y(1)$则表示母亲孕期吸烟组婴儿的出生体重.因为我们关心的是母亲吸烟对婴儿出生体重的分位数处理效应如何随母亲年龄的变化而变化, 因此这里的条件变量$Z$是母亲的年龄.图 1展示的是婴儿出生体重的核密度估计, 左右两图分别代表白人和黑人的估计结果.表 3则给出了白人和黑人婴儿出生体重分布的偏度与峰度估计结果以及检验$Y(0)$和$Y(1)$的分布是否对称的检验结果.根据这些结果, 我们可以发现, 不管是对于白人还是黑人来说, 婴儿出生体重的分布都是偏向左边的厚尾分布.基于此, 我们更应该考虑母亲吸烟对婴儿出生体重的分布效应而不仅仅是均值效应.

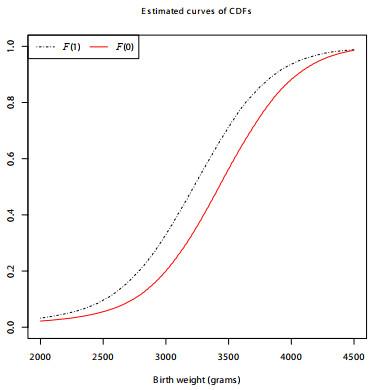
为了估计部分条件分位数处理效应函数$\Delta_{\tau}(z)$, 我们首先需要估计$p(x)$.为此, 我们使用与Abrevaya et al. (2015)中同样的协变量$X$, 有关这些协变量的具体内容可参看Abrevaya et al. (2015).由于$D$是一个二元变量, 与Abrevaya et al. (2015)中一样, 我们选择为倾向得分函数$p(x)$设定一个logit模型且对估计得到的$\widehat{p}_{n}(x)$进行截断使其位于$[0.01, 0.99]$.最后, 我们估计母亲年龄在20到30岁之间的部分条件分位数处理效应函数$\Delta_{\tau}(z)$.

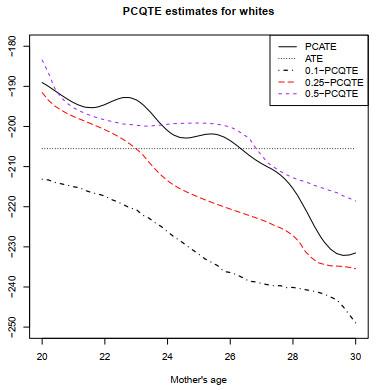
图 2给出了给定母亲年龄$(z=26)$下白人婴儿出生体重的条件累积分布函数的估计, 类似地, 我们也可得到给定其它年龄下婴儿出生体重的条件累积分布函数的估计结果.根据图 2中的估计结果, 我们可观察到$Y(1)$的条件累积分布函数的估计曲线位于$Y(0)$的条件累积分布函数估计曲线的左边, 这意味着在所有分位数水平下, 部分条件分位数处理效应的估计值应该取负值.

图 3给出的是在三个不同分位数水平$\tau=0.10$ (点虚线), $\tau=0.25$(长虚线)和$\tau=0.50$ (短虚线)下, 白人的部分条件分位数处理效应如何随母亲年龄变化而变化的估计结果.作为比较, 我们在图 3中也给出了Abrevaya et al. (2015), Lee et al. (2017)中考虑的PCATE (由实线表示) 以及无条件平均处理效应(average treatment effect, ATE) (由虚线表示) 的估计结果.根据图 3中的估计结果, 我们首先可观察到对于三个不同的分位数水平, $\widehat{\Delta}_{\tau}(z)$似乎都是随母亲年龄线性变化的².特别地, 估计结果$\widehat{\Delta}_{0.5}(z)$与估计的PCATE曲线是相似的但并不完全一样.事实上, $\widehat{\Delta}_{0.5}(z)$比PCATE的估计稍微大一点.其次, 我们可观察到, 在不同年龄下以及在所有分位数水平下, 母亲吸烟对婴儿出生体重都具有显著的负效应, 这与图 2中得到的发现是一致的.此外, 图 3中的估计结果也表明部分条件分位数处理效应在不同的母亲年龄组之间表现出实质性的异质性.总的来说, 当母亲年龄增大时, 估计的部分条件分位数处理效应在数值上会增大.另一方面, 在给定同样的年龄下, 部分条件分位数处理效应的估计值(在数值上) 在低分位数水平上比中位数或更高分位数水平上的估计值(在数值上) 要大.

²在最近的文章中, Tang, Cai and Fang et al. (2021)也使用这组数据考察了给定不同母亲年龄下, 母亲吸烟对婴儿出生体重的分位数处理效应是如何随母亲年龄的变化而变化的, 其得到的实证结果与本文相似.特别地, Tang et al. (2021)考虑了为$\Delta_{\tau}(z)$设定一个参数模型从而使用参数方法估计$\Delta_{\tau}(z)$, 而在本文, 我们并未为$\Delta_{\tau}(z)$设定任何模型且使用非参数方法估计$\Delta_{\tau}(z)$, 因此模型更具灵活性, 有关更多细节见Tang et al.(2021).

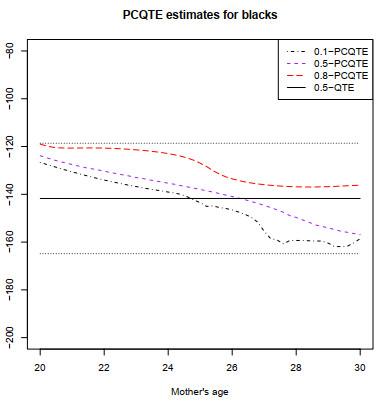
图 4给出的则是在三个不同分位数水平$\tau=0.10$ (点虚线), $\tau=0.50$ (短虚线)和$\tau=0.80$ (长虚线)下, 黑人的部分条件分位数处理效应如何随母亲年龄变化而变化的估计结果.此外, 我们在图 3中也给出了$\tau=0.50$水平下无条件分位数处理效应(由实线表示)以及它的$95\%$置信区间(由虚线表示) 的估计结果(根据Firpo (2007)方法计算而得).根据图 4中的估计结果, 我们可清楚地发现PCQTE的估计值也会随着母亲年龄的增加而稍微增大(在数值上), 但代表不同分位数水平的三条PCQTE曲线较为接近, 并且几乎都位于$\tau=0.50$的无条件分位数处理效应的$95\%$置信区间内.换言之, 和白人的情况完全不同, 对于黑人而言, 三个不同分位数水平的$\widehat{\Delta}_{\tau}(z)$可能并不随母亲年龄的变化而显著变化.

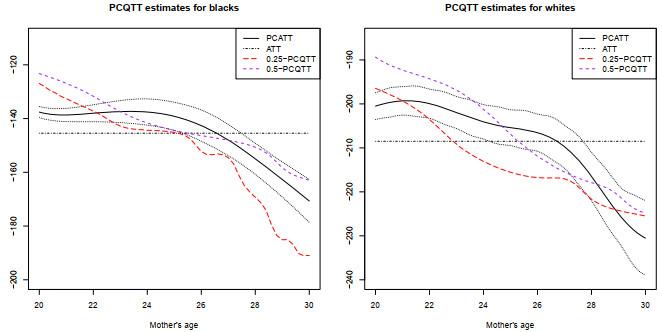
最后, 除了上面考虑的PCQTE的估计之外, 我们也考虑了PCQTT的估计, 其估计结果展示在图 5中, 其中左图是白人的估计结果, 而右图则是黑人的估计结果.在图 5中, 我们考虑了在两个不同的分位数水平$\tau=0.25(长虚线)$和$\tau=0.50(短虚线)$下 PCQTT 的估计.为了易于比较, 我们在图 5中也给出了处理组的部分条件平均处理效应(PCATT, 由实线表示) 及其$95\%$的置信区间 (由虚线表示)的估计结果, 同时还给出了处理组的无条件平均处理效应 (由点虚线表示)的估计结果.根据图 5 中的估计结果, 我们可观察到对于所考虑的两条PCQTT 估计曲线, PCQTT在不同的母亲年龄组之间存在异质性.具体而言, 对于考虑的两个不同分位数水平$\tau$值, $\widehat{\Delta}_{\tau|D=1}(z)$的数值会随着母亲年龄的增大而增加, 也就是说, 当母亲年龄变大时, 估计的分位数效应在数值上会变得更大.而对于给定母亲年龄时, PCQTT 点估计的数值在低分位数水平下比中位数水平下更大.

为了刻画分位数处理效应在由某一协变量定义的不同子群体之间的异质性, 我们提出了一个函数型参数—部分条件分位数处理效应, 并考虑了它的识别与估计.我们提出了一种新的估计方法并建立了其渐近性质.使用我们所提出的半参数估计方法, 我们估计了在给定不同年龄条件下, 母亲在怀孕期间吸烟对婴儿出生体重的分位数处理效应.根据实证结果, 我们发现总体而言, 当母亲年龄较大或者是在较低低分位数水平时, 吸烟对婴儿出生体重有更为严重的负效应.白人群体的条件分位数处理效应会随着母亲年龄的变化而变化, 但对黑人来说并非如此.

基于以上实证结果, 研究者可进一步探讨分位数处理效应是否随协变量$Z$而变化.为此, 下一步研究可考虑以下的假设检验问题:

$H_0: \Delta_\tau(z)=\Delta_\tau\quad \text{对所有的 $z\in\mathcal{Z}$} \quad \text{versus}\quad H_1:\Delta_\tau(z)\not=\Delta_\tau \quad \text{对某一 $z\in\mathcal{Z}$}, $

其中$\Delta_\tau$是$\tau$无条件分位数处理效应, $\mathcal{Z}$是$Z$的支撑集.在原假设之下, 对于所有的$z$值, 部分条件分位数处理效应都等于相应的无条件分位数处理效应, 而在备择假设下, 则至少存在某一$z$值使得部分条件分位数处理效应不同于无条件分位数处理效应.

数学证明

在正文中, 我们有$W_0(X_i, D_i)=\frac{1-D_i}{1-p(X_i)}$, $W_1(X_i, D_i)=\frac{D_i}{p(X_i)}$和$\widehat{W}_{n, 0}(X_i, D_i)=\frac{1-D_i}{1-\widehat{p}_n(X_i)}$, $\widehat{W}_{n, 1}(X_i, D_i)=\frac{D_i}{\widehat{p}_n(X_i)}$, 其中$\widehat{p}_n(x)=p(x; \widehat{\theta}_n)$是使用数据$(X_i, D_i)$, $i=1, \cdots, n$估计得到的倾向得分函数.为了证明定理1, 我们需要下面的引理.

引理 1  对于$j=0$或$1$, 考虑随机函数:

$\Gamma_{n, j}(q, z)=\sum\limits_{i=1}^{n}hK_{h, i}(z)\widehat{W}_{n, j}(X_i, D_i)\Big[\rho_{\tau}(Y_{i};q)-\rho_{\tau}\big(Y_{i};q_{j, \tau}(z)\big)\Big]$

和

$\begin{array}{l}{{\tilde \Gamma }_{n, j}}(q, z) = \sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i}){\varphi _\tau }({Y_i};{q_{j, \tau }}(z))(q - {q_{j, \tau }}(z)) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot nh{(q - {q_{j, \tau }}(z))^2}, \end{array}$

其中$K_{h, i}(z)=K\big((Z_{i}-z)/h\big)/h$和$\varphi_{\tau}(y;q)=I(y\leq q)-\tau$.在假设1$\sim$5下, 对任意的$z\in \mathcal{Z}$和任意的$\varepsilon>0$, 我们有:

$\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |{\Gamma _{n, j}}(q, z) - {\tilde \Gamma _{n, j}}(q, z)| = {o_p}(1).$

引理 1 的证明  根据$\rho_{\tau}(y;q)$和$\varphi_{\tau}(y;q)$的定义, 我们知:

$\begin{array}{l}{\Gamma _{n, j}}(q, z) = \sum\limits_{i = 1}^n h {K_{h, i}}(z){{\hat W}_{n, j}}({X_i}, {D_i})[{\varphi _\tau }({Y_i};{q_{j, \tau }}(z))(q - {q_{j, \tau }}(z)) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({Y_i} - q)(I\{ {Y_i} \le {q_{j, \tau }}(z)\} - I\{ {Y_i} \le q\})].\end{array}$

因此,

(A.1) $\begin{array}{l}\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |{\Gamma _{n, j}}(q, z) - {\Gamma _{n, j}}(q, z)|\\ \le \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } \{ |q - {q_{j, \tau }}(z)| \cdot \sum\limits_{i = 1}^n h {K_{h, i}}(z) \cdot |{{\hat W}_{n, j}}({X_i}, {D_i}) - {W_j}({X_i}, {D_i})| \cdot |{\varphi _\tau }({Y_i};{q_{j, \tau }}(z))|\} + \\\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\sum\limits_{i = 1}^n h {K_{h, i}}(z){{\hat W}_{n, j}}({X_i}, {D_i})({Y_i} - q)(I\{ {Y_i} \le {q_{j, \tau }}(z)\} - I\{ {Y_i} \le q\}) - \\\frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot nh{(q - {q_{j, \tau }}(z))^2}|\\: = {{\cal A}_1} + {{\cal A}_2}.\end{array}$

首先, 我们考虑$\mathcal{A}_1$.注意到$\sup_{x\in \mathcal{X}}\Big|\widehat{W}_{n, j}(x, D_i)-W_j(x, D_i)\Big|=O_p(n^{-1/2})$和$\Big|\varphi_{\tau}\big(Y_i;q_{j, \tau}(z)\big)\Big|$是有界的, 由此容易得到:

$\begin{array}{l}{{\cal A}_1} = \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } \{ |q - {q_{j, \tau }}(z)| \cdot \sum\limits_{i = 1}^n h {K_{h, i}}(z) \cdot |{{\hat W}_{n, j}}({X_i}, {D_i}) - {W_j}({X_i}, {D_i})| \cdot |{\varphi _\tau }({Y_i};{q_{j, \tau }}(z))|\} \le \\\;\;\frac{\varepsilon }{{\sqrt {nh} }} \cdot \sum\limits_{i = 1}^n h {K_{h, i}}(z) \cdot {O_p}({h^{ - 1/2}}) \cdot O(1) = {O_p}({h^{1/2}}) \cdot \frac{1}{n}\sum\limits_{i = 1}^n {{K_{h, i}}} (z).\end{array}$

因为$ \frac{1}{n} \sum_{i=1}^{n}K_{h, i}=O_p(1)$, 因此容易证明:

(A.2) ${{\cal A}_1} = {O_p}({h^{1/2}}) \cdot {O_p}(1) = {o_p}(1).$

现在, 我们考虑$\mathcal{A}_2$.定义$\Psi(y; q_1, q_2) =(y-q_1)\big(I\{y\leq q_2\}-I\{y\leq q_1\}\big)$, 那么我们有:

$\begin{array}{l}{{\cal A}_2} = \\\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\sum\limits_{i = 1}^n h {K_{h, i}}(z){{\hat W}_{n, j}}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z)) - \frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot nh{(q - {q_{j, \tau }}(z))^2}|\\ \le \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\sum\limits_{i = 1}^n h {K_{h, i}}(z)[{{\hat W}_{n, j}}({X_i}, {D_i}) - {W_j}({X_i}, {D_i})]\Psi ({Y_i};q, {q_{j, \tau }}(z))| + \\\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z)) - \frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot nh{(q - {q_{j, \tau }}(z))^2}|\\: = {{\cal A}_{21}} + {{\cal A}_{22}}.\end{array}$

注意到,

$\begin{array}{l}\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\Psi ({Y_i};q, {q_{j, \tau }}(z)| = \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |({Y_i} - q)(I\{ {Y_i} \le {q_{j, \tau }}(z)\} - I\{ {Y_i} \le q\})|\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |q - {q_{j, \tau }}(z)| = \varepsilon /\sqrt {nh} .\end{array}$

根据证明$\mathcal{A}_1 =o_p(1)$类似的步骤, 我们也可以证明$\mathcal{A}_{21} =o_p(1)$. 接下来, 我们考虑$\mathcal{A}_{22}$中的$\sum_{i=1}^n hK_{h, i}(z)W_j(X_i, D_i) \Psi(Y_i; q, q_{j, \tau}(z))$.事实上,

$\begin{array}{l}\;\;\;\;E\left[ {\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))} \right]\\ = nE[h{K_{h, i}}(z)\Psi ({Y_i}(j);q, {q_{j, \tau }}(z))]\\ = nh \cdot E\{ {K_{h, i}}(z)E[({Y_i}(j) - q)(I\{ {Y_i}(j) \le {q_{j, \tau }}(z)\} - I\{ {Y_i}(j) \le q\})|{Z_i}]\} \\ = nh \cdot E\{ {K_{h, i}}(z)\int_q^{{q_{j, \tau }}(z)} {(y - q)} {\mkern 1mu} {f_{Y(j)|Z}}(y|{Z_i}){\mkern 1mu} {\rm{d}}y\} \\ = nh \cdot E\{ {K_{h, i}}(z)\int_q^{{q_{j, \tau }}(z)} {(y - q)} {\mkern 1mu} [{f_{Y(j)|Z}}({q_{j, \tau }}(z)|{Z_i}) + O(|{q_{j, \tau }}(z) - q|)]{\mkern 1mu} {\rm{d}}y\} \\ = nh \cdot \frac{{{{({q_{j, \tau }}(z) - q)}^2}}}{2} \cdot E\{ {K_{h, i}}(z)[{f_{Y(j)|Z}}({q_{j, \tau }}(z)|{Z_i}) + O(|{q_{j, \tau }}(z) - q|)]\} \\ = nh \cdot \frac{{{{({q_{j, \tau }}(z) - q)}^2}}}{2} \cdot [{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z) + O(|{q_{j, \tau }}(z) - q|) + o(1)]\end{array}$

和

$\begin{array}{l}\;\;\;{\rm{Var}}\left[ {\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))} \right]\\ = n{\rm{Var}}[h{K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))]\\ \le n \cdot E{[h{K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))]^2}\\ = n{h^2} \cdot E{[{K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))]^2}\\ = nh \cdot O(1) \cdot E\{ h{\mkern 1mu} K_{h, i}^2(z)E[{({Y_i}(j) - q)^2}{(I\{ {Y_i}(j) \le {q_{j, \tau }}(z)\} - I\{ {Y_i}(j) \le q\})^2}|{Z_i}]\} \\ = nh \cdot O(1) \cdot E\{ h{\mkern 1mu} K_{h, i}^2(z) \cdot |\int_q^{{q_{j, \tau }}(z)} {{{(y - q)}^2}} {\mkern 1mu} {f_{Y(j)|Z}}(y|{Z_i}){\mkern 1mu} {\rm{d}}y|\} \\ = nh \cdot O(1) \cdot O(|{q_{j, \tau }}(z) - q{|^3}).\end{array}$

因此, 我们可以得到:

$\begin{array}{l}\;\;\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))\\ = E\left[ {\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))} \right] + \\\;\;\;{O_p}{\left({{\rm{Var}}\left[ {\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z))} \right]} \right)^{1/2}}\\ = nh \cdot \frac{{{{({q_{j, \tau }}(z) - q)}^2}}}{2} \cdot [{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z) + O(|{q_{j, \tau }}(z) - q|) + o(1)] + \\{\mkern 1mu} \;\;\;{O_p}{(nh \cdot |{q_{j, \tau }}(z) - q{|^3})^{1/2}}\end{array}$

和

$\begin{array}{l}{{\cal A}_{22}} = \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |\sum\limits_{i = 1}^n h {K_{h, i}}(z){W_j}({X_i}, {D_i})\Psi ({Y_i};q, {q_{j, \tau }}(z)) - \\\;\;\;\;\;\;\;\;\frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot nh \cdot {(q - {q_{j, \tau }}(z))^2}|\\\;\;\;\;\;\;\;\; = \mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |nh \cdot \frac{{{{({q_{j, \tau }}(z) - q)}^2}}}{2} \cdot [O(|{q_{j, \tau }}(z) - q|) + o(1)] + {\mkern 1mu} {O_p}{(nh \cdot |{q_{j, \tau }}(z) - q{|^3})^{1/2}}|\\\;\;\;\;\;\;\;\; = {o_p}(1).\end{array}$

于是, 我们有下面的结果:

(A.3) ${{\cal A}_2} = {{\cal A}_{21}} + {{\cal A}_{22}} = {o_p}(1).$

根据(A.1, A.2和A.3), 我们有:

(33) $\mathop {\sup }\limits_{|q - {q_{j, \tau }}(z)| \le \varepsilon /\sqrt {nh} } |{\Gamma _{n, j}}(q, z) - {\tilde \Gamma _{n, j}}(q, z)| = {o_p}(1).$

定理 1 的证明 对于$j=0$或$1$, 我们首先考虑:

$\begin{array}{l}{{\tilde q}_{j, \tau }}(z) = \arg {\min _q}\{ {\Gamma _{n, j}}(q, z)\} \\\;\;\;\;\;\;\;\;\;\; = {q_{j, \tau }}(z) - \frac{1}{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}} \cdot \frac{1}{n}\sum\limits_{i = 1}^n {{K_{h, i}}} (z){W_j}({X_i}, {D_i}){\varphi _\tau }({Y_i};{q_{j, \tau }}(z))\\\;\;\;\;\;\;\;\;\;\; = {q_{j, \tau }}(z) - \frac{1}{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}} \cdot \frac{1}{n}\sum\limits_{i = 1}^n {{K_{h, i}}} (z){\psi _j}({Y_i}, {X_i}, {D_i};z).\end{array}$

由简单计算可得:

$E({\tilde q_{j, \tau }}(z)) = {q_{j, \tau }}(z) - \frac{{{h^2}}}{2}{\mu _2}(K){\delta _{j, \tau }}(z) + o({h^2}), $

其中$\mu_{2}(K)=\int u^{2}K(u){\rm d}u$和

${\delta _{j, \tau }}(z) = \frac{{2{f_{Z'}}(z)\frac{{\partial {F_{Y(j)|Z}}({q_{j, \tau }}(z)|u)}}{{\partial u}}{|_{u = z}} + {f_Z}(z)\frac{{{\partial ^2}{F_{Y(j)|Z}}({q_{j, \tau }}(z)|u)}}{{\partial {u^2}}}{|_{u = z}}}}{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}, $

由此得到:

(A.4) $\begin{array}{l}\;\;\;\sqrt {nh} ({{\tilde q}_{j, \tau }}(z) - E({{\tilde q}_{j, \tau }}(z))) = \sqrt {nh} \left({{{\tilde q}_{j, \tau }}(z) - {q_{j, \tau }} + \frac{{{h^2}}}{2}{\mu _2}(K){\delta _{j, \tau }}(z) + o({h^2})} \right) - \\ = \frac{1}{{\sqrt {nh} }}\frac{1}{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}} \times \\\;\;\;\;\sum\limits_{i = 1}^n [ h{K_{h, i}}(z){\psi _j}({Y_i}, {X_i}, {D_i};z) - E(h{K_{h, i}}(z){\psi _j}({Y_i}, {X_i}, {D_i};z))].\end{array}$

接下来我们考虑$\widetilde{q}_{j, \tau}(z)$和$\widehat{q}_{j, \tau}(z)$的差, 其中,

$\begin{array}{l}{{\hat q}_{j, \tau }}(z) = \arg {\min _q}\sum\limits_{i = 1}^n h {K_{h, i}}(z){{\hat W}_{n, j}}({X_i}, {D_i}){\rho _\tau }({Y_i};q)\\\;\;\;\;\;\;\;\;\; = \arg {\min _q}\sum\limits_{i = 1}^n h {K_{h, i}}(z){{\hat W}_{n, j}}({X_i}, {D_i})[{\rho _\tau }({Y_i};q) - {\rho _\tau }({Y_i};{q_{j, \tau }}(z))]\\\;\;\;\;\;\;\;\;\; = \arg {\min _q}\{ {\Gamma _{n, j}}(q, z)\} .\end{array}$

因为$\Gamma_{n, j}(q, z)$关于$q$是凸函数, 容易证明对任意的$\epsilon>0$和$|q-\widetilde{q}_{j, \tau}(z)|>\epsilon/\sqrt{nh}$,

$\left({1 - \frac{{ \in /\sqrt {nh} }}{{|q - {{\tilde q}_{j, \tau }}(z)|}}} \right){\Gamma _{n, j}}({\tilde q_{j, \tau }}(z), z) + \frac{{ \in /\sqrt {nh} }}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} {\Gamma _{n, j}}(q, z) \ge {\Gamma _{n, j}}\left({{{\tilde q}_{j, \tau }}(z) + \frac{{q - {{\tilde q}_{j, \tau }}(z)}}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} \frac{ \in }{{\sqrt {nh} }}, z} \right).$

因此, 对所有的$|q-\widetilde{q}_{j, \tau}(z)|>\epsilon/\sqrt{nh}$,

$\begin{array}{l}\frac{{ \in /\sqrt {nh} }}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} [{\Gamma _{n, j}}(q, z) - {\Gamma _{n, j}}({{\tilde q}_{j, \tau }}(z), z)]\\ \ge {\Gamma _{n, j}}\left({{{\tilde q}_{j, \tau }}(z) + \frac{{q - {{\tilde q}_{j, \tau }}(z)}}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} \frac{ \in }{{\sqrt {nh} }}, z} \right) - {\Gamma _{n, j}}({{\tilde q}_{j, \tau }}(z), z)\\ \ge {{\tilde \Gamma }_{n, j}}{\rm{(}}{{\tilde q}_{j, \tau }}(z) + \frac{{q - {{\tilde q}_{j, \tau }}(z)}}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} \frac{ \in }{{\sqrt {nh} }}, z) - {{\tilde \Gamma }_{n, j}}({{\tilde q}_{j, \tau }}(z), z)\\\;\;\; - 2\mathop {\sup }\limits_{|u - {{\tilde q}_{j, \tau }}(z)| \le \in /\sqrt {nh} } |{\Gamma _{n, j}}(u, z) - {{\tilde \Gamma }_{n, j}}(u, z)|.\end{array}$

注意到$\widetilde{\Gamma}_{n, j}(q, z)$是关于$q$的二次函数以及$\widetilde{q}_{j, \tau}(z)=\arg\min_{q}\big\{\widetilde{\Gamma}_{n, j}(q, z) \big\}$.那么, 对所有的$|q-\widetilde{q}_{j, \tau}(z)|>\epsilon/\sqrt{nh}$, 有:

$\begin{array}{l}\;\;\;\frac{{ \in /\sqrt {nh} }}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} [{\Gamma _{n, j}}(q, z) - {\Gamma _{n, j}}({{\tilde q}_{j, \tau }}(z), z)]\\ \ge \frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot { \in ^2} - 2\mathop {\sup }\limits_{|u - {{\tilde q}_{j, \tau }}(z)| \le \in /\sqrt {nh} } |{\Gamma _{n, j}}(u, z) - {{\tilde \Gamma }_{n, j}}(u, z)|\\ \ge \frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot { \in ^2} - 2\mathop {\sup }\limits_{|u - {q_{j, \tau }}(z)| \le \in /\sqrt {nh} + |{q_{j, \tau }}(z) - {{\tilde q}_{j, \tau }}(z)|} |{\Gamma _{n, j}}(u, z) - {{\tilde \Gamma }_{n, j}}(u, z)|.\end{array}$

从(A.4) 知$|q_{j, \tau}(z)-\widetilde{q}_{j, \tau}(z)|=O_p(1/\sqrt{nh})$, 这加上假设4以及引理1, 我们有:

$\frac{{ \in /\sqrt {nh} }}{{|q - {{\tilde q}_{j, \tau }}(z)|}}{\mkern 1mu} [{\Gamma _{n, j}}(q, z) - {\Gamma _{n, j}}({\tilde q_{j, \tau }}(z), z)] \ge \frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot { \in ^2} + {o_p}(1)$

对所有的$|q-\widetilde{q}_{j, \tau}(z)|>\epsilon/\sqrt{nh}$成立.由$\widehat{q}_{j, \tau}(z)$的定义$\widehat{q}_{j, \tau}(z)=\arg\min_q\big\{\Gamma_{n, j}\big(q, z\big)\big\}$知$\Gamma_{n, j}\big(\widehat{q}_{j, \tau}(z), z\big) -\Gamma_{n, j}\big(\widetilde{q}_{j, \tau}(z), z\big)\leq0$, 于是我们可以证明:

$\begin{array}{l}\;\;\;\;P(\sqrt {nh} |{{\hat q}_{j, \tau }}(z) - {{\tilde q}_{j, \tau }}(z)| > \in)\\ \le P(\mathop {\inf }\limits_{|q - {{\tilde q}_{j, \tau }}(z)| > \in /\sqrt {nh} } \{ {\Gamma _{n, j}}(q, z) - {\Gamma _{n, j}}({{\tilde q}_{j, \tau }}(z), z)\} \le 0)\\ \le P(\frac{{{f_Z}(z){f_{Y(j)|Z}}({q_{j, \tau }}(z)|z)}}{2} \cdot { \in ^2} + {o_p}(1) \le 0) \to 0, \end{array}$

这意味着$\widehat{q}_{j, \tau}(z)=\widetilde{q}_{j, \tau}(z) +o_p(1/\sqrt{nh})$.根据(A.4)和$\widehat{q}_{j, \tau}(z)=\widetilde{q}_{j, \tau}(z) +o_p(1/\sqrt{nh})$, 知

$\begin{array}{l}\;\;\;\;\;\;\sqrt {nh} \left[ {{{\hat \Delta }_\tau }(z) - {\Delta _\tau }(z) + \frac{{{h^2}}}{2}{\mu _2}(K){\delta _\tau }(z) + {o_p}({h^2})} \right]\\\;\;\;\;\;\;\sqrt {nh} \left[ {{{\tilde \Delta }_\tau }(z) - {\Delta _\tau }(z) + \frac{{{h^2}}}{2}{\mu _2}(K){\delta _\tau }(z) + {o_p}({h^2}) + {{\hat \Delta }_\tau }(z) - {{\tilde \Delta }_\tau }(z)} \right]\\ = - \frac{1}{{\sqrt {nh} }}\frac{1}{{{f_Z}(z)}}\sum\limits_{i = 1}^n \{ \frac{{h{K_{h, i}}(z){\psi _1}({Y_i}, {X_i}, {D_i}, z) - E(h{K_{h, i}}(z){\psi _1}({Y_i}, {X_i}, {D_i}, z))}}{{{f_{Y(1)|Z}}({q_{1, \tau }}(z)|z)}}\\ - \frac{{h{K_{h, i}}(z){\psi _0}({Y_i}, {X_i}, {D_i}, z) - E(h{K_{h, i}}(z){\psi _0}({Y_i}, {X_i}, {D_i}, z))}}{{{f_{Y(0)|Z}}({q_{0, \tau }}(z)|z)}}\} + {o_p}(1), \end{array}$

其中$\widetilde{\Delta}_{\tau}(z)=\widetilde{q}_{1, \tau}(z)-\widetilde{q}_{0, \tau}(z)$.由以下事实:

$E[h{K_{h, i}}(z){\psi _j}({Y_i}, {X_i}, {D_i};z) - E(h{K_{h, i}}(z){\psi _j}({Y_i}, {X_i}, {D_i};z))] = 0, $

和Lyapunov中心极限定理, 容易证明:

$\sqrt {nh} \left[ {{{\hat \Delta }_\tau }(z) - {\Delta _\tau }(z) + \frac{{{h^2}}}{2}{\mu _2}(K){\delta _\tau }(z) + {o_p}({h^2})} \right]\mathop \to \limits^D {\cal N}(0, ||K||_2^2\sigma _\tau ^2(z)/{f_Z}(z)).$

至此, 我们完成了定理的证明.