非平稳时间序列在经济、金融、气候科学等相关领域随处可见, 比如可支配性收入和支出, 股票价格和二氧化碳的排放量. 在过去大约二十年时间里, 非平稳时间序列的极限理论受到密切关注和长足发展, 尤其是在非线性参数模型和非参数模型的估计和检验方面, 比如, 非线性参数模型的估计理论Park and Phillips (2001), 自回归模型识别性检验Gao, King and Lu et al. (2009a), 非线性时间序列模型的非参数检验Gao, King and Lu et al. (2009b), 非参数核估计理论Wang and Phillips (2009a), 部分线性单指标非平稳时间序列模型Dong, Gao and Tjøstheim (2016), 正交级数驱动非平稳时间序列模型的识别性检验Dong and Gao (2018), 非参数可加且具有时间趋势、平稳变量和非平稳变量的回归模型Dong and Linton (2018)和非平稳变系数面板数据模型Dong, Gao and Peng (2020), 仅列举一部分.F

筛分法(sieve method)是计量经济学重要的非参数方法之一, 它和核方法(kernel method) 都是常用的非参数方法, 但较之于核方法, 筛分法在使用上具有高度的灵活性, 在性质上具有全局性而非局部性的特点. 筛分法的名称首先由Grenander (1981)采用, 它使用一个函数系的线性组合在某种数学意义下逼近未知函数, 这种组合构成的空间在文献里就称为线性筛分空间(linear sieve space); 通常, 筛分法使用的函数系包括正交多项式系, 正交三角多项式系, B-样条, 小波和神经网络等等. 筛分法几乎可以在计量经济学所有涉及非参数和半参数的各个领域使用, 比如非参数回归, 极大似然估计, 工具变量法和广义矩方法等等. 关于非参数方法和筛分法请读者参考Rao (1983), Chen and Shen (1998), Gao (2007), Chen (2007), Li and Racine (2007). 本文讨论的筛分法仅限于未知函数的正交级数展开, 严格来讲属于级数估计方法(series estimation), 我们习惯上仍然称之为筛分法.

计量经济学非参数问题中的未知函数通常来自于$ L^2 $空间和$ C $空间. 在数学上, $ L^2 $空间属于希尔伯特空间, 以正交函数系为基, 从而空间里每一个函数都可以表示为无穷正交级数, 其部分和按模收敛于该函数(在某些条件下还可以逐点收敛), 这为筛分法提供了数学基础; 另外, $ C $空间就是连续函数空间; 根据熟知的Weierstrass逼近定理, 多项式系在具有紧支集的$ C $空间里稠密, 从而可以用多项式来逼近其中的未知函数. 但是人们发现, 直接使用多项式作为筛分空间在计量理论上会有一定缺陷. 关于这一点我们将在第二节的最后部分做适当讨论.

一般地, 空间$ L^2([a, b], \rho(x)) $为定义于$ [a, b] $上, 关于密度$ \rho(x) $平方可积的函数集合:

$ \begin{equation*} L^2([a, b], \rho(x))=\left\{f(x):\ \int_a^bf^2(x)\rho(x){\rm d}x<\infty\right\}, \end{equation*} $

这里, $ [a, b] $可以是有界区间, 也可以是无穷区间, 比如$ (-\infty, \infty) $和$ [0, \infty) $. 所谓定义于$ [a, b] $上的密度函数即是非负的且集合$ \{x: \rho(x)=0, x\in[a, b]\} $的勒贝格测度为零的函数, 最好满足$ \int_a^b\rho(x){\rmd}x=1 $, 但这不是必须的. 可以说, 决定空间$ L^2([a, b], \rho(x)) $的两个要素: 一是区间$ [a, b] $, 二是密度函数$ \rho(x) $; 有了这两个要素, 这个空间以及刻画它的重要概念如内积, 模和正交性等等都相应地被确定了. 这对使用筛分法时基函数的选取具有指导意义.

在使用筛分法时, 大多数情况下人们都没有明确的线索来确定这两个要素. 就区间而言, 许多现有的文献只考虑有界区间, 比如Newey (1997)中假设8和Ai and Chen (2003, p1803)中假设3.1; 这样的考虑多数情况下是出于简单化的目的. 然而, 这种限制却排除了许多重要的变量, 比如正态随机变量或者服从于指数分布的随机变量; 另外一种被排除的情形是, 当观测值随着样本容量的增大而发散, 非参数函数的定义域就不会包含于任何有界区间. 例如, 假设$ \{x_t\} $是一个单位根过程, 则有$ x_t=O_P(\sqrt{t}) $; 倘若我们要估计的非参数在研究的问题中以$ g(x_t) $出现, 则表明$ g(x) $的定义域无界.

为了弥补文献中的这种缺憾, 最近几年研究者们做出了一系列努力. Chen and Christensen (2015)考虑$ [-a_n, a_n](a_n\to +\infty) $上的筛分法, 逐渐地从有限区间过渡到无限区间; 系列文章Dong, Gao and Peng (2015), Dong, Gao and Tjøstheim (2016), Dong and Linton (2018), Dong and Gao(2018, 2019), Dong, Linton and Peng (2021)则直接采用了无穷区间的筛分法, 得到非参数函数的估计量, 建立了相关的渐近理论, 并适当的讨论了实证应用; 另外, 朱平芳等(2020)将这些理论结果应用于汇率预测问题, 为解决汇率预测提供了新的思路.

本文目的有两个: 一是总结筛分法最近发展; 二是回顾非参数非平稳协整模型部分最新结果. 文章在第2节总结了筛分法的数学基础知识, 并指出在使用筛分法时几个关键量和应该回避问题; 文章第3.1节介绍了部分线性单指标非平稳模型的估计和渐近理论, 并使用蒙特卡罗模拟实验验证理论结果; 第3.2节介绍了非平稳非参数时间序列模型识别性检验, 而检验统计量是通过正交级数构造的; 第3.3节介绍了非参数可加非平稳时间序列模型的估计和渐近理论, 而模型的协变量包括三种类型的变量, 即时间变量, 平稳变量和单位根过程, 并将理论结果应用于股市的配对交易策略, 产生较好的结果. 虽然平稳变量的支撑集可能有界也可能无界, 但非平稳变量的支撑集一定是无界的, 所以第3节所有模型都涉及到无界区间上的筛分法. 第4节是结束语.

对于任意的$ f_1(x), f_2(x), f(x)\in L^2([a, b], \rho(x)) $, 定义内积运算以及由它诱导的模如下:

$ \begin{equation*} \langle f_1, f_2\rangle=\int_a^bf_1(x)f_2(x)\rho(x){\rm d}x, \qquad \|f\|=\sqrt{ \langle f, f\rangle}, \end{equation*} $

则空间$ L^2([a, b], \rho(x)) $和这个内积一并构成了一个希尔伯特空间. 如果$ \langle f_1, f_2\rangle=0 $, 则称$ f_1(x) $和$ f_2(x) $是正交的. 如果在$ L^2([a, b], \rho(x)) $中, 一个函数序列$ \{\varphi_j(x), j\ge0\} $的元素两两正交, 则称它是一个正交系; 在此基础上若$ \|\varphi_j\|=1 $对所有$ j $成立, 则称$ \{\varphi_j(x), j\ge 0\} $为标准正交系; 如果再加上完备性, 则$ \{\varphi_j(x), j\ge0\} $形成了该空间的标准正交基. 根据希尔伯特空间理论, 如果$ \{\varphi_j(x), j\ge 0\} $为$ L^2([a, b], \rho(x)) $的标准正交基, 对于任何$ g(x)\in L^2([a, b], \rho(x)) $有:

(1) $ \begin{equation} g(x)=\sum\limits_{j=0}^\infty c_j\varphi_j(x), \qquad c_j=\langle g, \varphi_j\rangle, \end{equation} $

这里, 无穷级数的收敛性是在模的意义下成立.

正交多项式系有两个主要来源: 一是Gram-Schmidt正交化方法, 二是微分算子特征函数(即Sturm-Liouville问题). 众所周知, 幂函数系$ \{x^j, j=0, 1, 2, \cdots\} $在任何区间上都是线性独立的, 利用正交性的定义, 通过Gram-Schmidt正交化方法, 我们可以得到$ L^2([a, b], \rho(x)) $的正交多项式序列; 并且可以证明, 该序列是完备的. 因此幂函数系经过Gram-Schmidt正交化和标准化后就是该空间的一组标准正交基. 请参考Szego (1975), 徐利治, 王仁宏和周蕴时(1983), Dudley (2003).

另一种产生正交多项式系的方法是微分方程求解, 或者说是某种微分算子的特征根与特征函数问题的解. 考虑超几何型微分方程:

$ \begin{equation*} s(x)y''+v(x)y'+\lambda y=0, \end{equation*} $

其中$ s(x) $和$ v(x) $分别是次数不超过二次和一次的多项式, $ \lambda $是与$ x $无关常数. 我们不加证明地给出下面引理.

引理2.1  对于任意非负整数$ n $, 下列超几何型微分方程:

$ \begin{equation*} s(x)y''+v(x)y'+\lambda_n y=0, \ \quad \lambda_n=-nv'(x)-\frac{n(n-1)}{2}s''(x), \end{equation*} $

具有多项式$ y_n\equiv y_n(x) $解. 再设, 存在密度函数$ \rho(x) $, 满足$ (s(x)\rho(x))'=v(x)\rho(x) $和边值条件:

$ \begin{equation*} s(x)\rho(x)x^k\Big |_{x=a, b}=0, \quad k=0, 1, 2, \cdots, \end{equation*} $

这里, $ a $和$ b $是函数$ \rho(x) $支撑集的边界点. 那么, 多项式解系$ \{y_n\} $在$ (a, b) $关于$ \rho(x) $正交.

人们通常会额外的要求密度函数$ \rho(x)>0 $和$ s(x)>0 $在$ (a, b) $成立; 引理2.1中, 多项式系$ y_n(x) $称为古典正交多项式系(classic orthogonal polynomial system), 随后我们给出一些例子. 另外还可以证明, $ y_n(x) $具有显式表达式:

$ \begin{equation*} y_n(x)=\frac{C_n}{\rho(x)}\frac{{\rm d}^n}{{\rm d}x^n}(s^n(x)\rho(x)), \end{equation*} $

其中$ C_n $是与$ n $有关常数. 这个公式在文献里称为Rodrigues公式, 纪念Rodrigues于1814年发现的勒让德多项式系(Legendre polynomials)的此种表达式, $ \rho(x)\equiv 1 $, $ s(x)=1-x^2 $. 请参考Nikiforov and Uvarov (1988).

例2.1  空间$ L^2[-1, 1] $中, $ \langle g_1(x), g_2(x)\rangle =\int_{-1}^1g_1(x)g_2(x){\rm d}x $. 勒让德多项式系(Legendre polynomials) $ \{P_n(x)\} $构成完备正交系, 且满足微分方程:

$ \begin{equation*} (1-x^2)y''-2xy'+n(n+1)y=0, \end{equation*} $

其Rodrigues公式为:

$ P_n(x)=\frac{1}{2^nn!}\frac{{\rm d}^n}{{\rm d}x^n}[(x^2-1)^n], $

正交性为:

$ \int_{-1}^1P_n(x)P_m(x){\rm d}x=\frac{2}{2n+1}\delta_{mn}, $

$ \delta_{mn}=1 $当$ m=n $; $ \delta_{mn}=0 $当$ m\ne n $. 另外有递推公式:

$ (n+1)P_{n+1}-(2n+1)xP_n+nP_{n-1}=0, $

和生成函数:

$ \frac{1}{\sqrt{1-2tx+t^2}}=\sum\limits_{j=0}^\infty P_n(x)t^j. $

勒让德多项式系满足有界性: $ |P_n(x)|\le 1 $, $ x\in[-1, 1] $.

例2.2  空间$ L^2([-1, 1], 1/\sqrt{1-x^2}) $, $ \langle g_1(x), g_2(x)\rangle= \int_{-1}^1g_1(x)g_2(x) /\sqrt{1-x^2}{\rm d}x. $在这个空间里, 第一类切比雪夫多项式系(Chebyshev polynomials of the first kind)构成完备正交系, 它具有三角多项式表达$ T_n(x)=\cos(n\, \arccos(x)) $和Rodrigues公式:

$ T_n(x)=\frac{(-1)^n}{(2n-1)!!}\sqrt{1-x^2} \frac{{\rm d}^n}{{\rm d}x^n}(1-x^2)^{n-1/2}, $

且有递推公式: $ T_0(x)=1 $, $ T_1(x)=x $,

$ T_{n+1}(x)=2xT_n(x)-T_{n-1}(x). $

其正交性为:

$ \begin{equation*} \int_{-1}^1 T_n(x)T_m(x)\frac{1}{\sqrt{1-x^2}}{\rm d}x=\begin{cases} 0, & m\ne n, \\ \pi, & m=n=0, \\ \frac{1}{2}\pi, & m=n\ne 0. \end{cases} \end{equation*} $

$ T_n $满足微分方程$ (1-x^2)y''-xy'+n^2y=0 $; 其生成函数为$ \frac{1-tx}{1-2tx+t^2}=\sum_{n=0}^\infty T_n(x)t^n $. 显然, $ |T_n(x)|\le 1 $.

例2.3  空间$ L^2(\mathbb{R}, \exp(-x^2/2)) $, $ \langle g_1(x), g_2(x)\rangle=\int g_1(x)g_2(x)\exp(-x^2/2){\rm d}x $. 这个空间足够大, 它包含任何多项式, 幂函数和任何有界函数, 可以满足计量经济学的理论研究和实证分析. 厄尔米特多项式系(Hermite polynomials)是其中的正交基, 它的Rodrigues表达式:

$ H_{n}(x)=(-1)^{n}\exp(x^{2}/2)\frac{{\rm d}^{n}}{{\rm d}x^{n}}\exp(-x^{2}/2), \qquad n\ge0, $

生成函数为:

$ \exp(xt-t^2/2)=\sum\limits_{n=0}^\infty H_n(x)\frac{t^n}{n!}. $

其正交性为:

$ \int H_n(x)H_m(x)\exp(-x^2/2){\rm d}x=\sqrt{2\pi}n!\delta_{nm}, $

且满足递推公式:

$ H_{n+1}(x)=xH_n(x)-H'_n(x), \qquad H_n'(x)=nH_{n-1}(x). $

例2.4  空间$ L^2(\mathbb{R}, \exp(-x^2)) $, $ \langle g_1(x), g_2(x)\rangle=\int g_1(x)g_2(x)\exp(-x^2){\rm d}x $. 这个空间较前一个例子更大, 因为它的密度的尾部更细. 该空间里也有一类称为厄尔米特多项式的正交系, 其Rodrigues表达式:

$ H_{n}(x)=(-1)^{n}\exp(x^{2})\frac{{\rm d}^{n}}{{\rm d}x^{n}}\exp(-x^{2}), \qquad n\ge0, $

生成函数为:

$ \exp(2xt-t^2)=\sum\limits_{n=0}^\infty H_n(x)\frac{t^n}{n!}, $

正交性为:

$ \langle H_n(x), H_m(x)\rangle=\sqrt{\pi}2^nn!\delta_{nm}. $

它满足递推公式:

$ H_{n+1}(x)=2xH_n(x)-2H'_n(x), \qquad H_n'(x)=2nH_{n-1}(x). $

例2.5  空间$ L^2(\mathbb{R}) $, $ \langle g_1(x), g_2(x)\rangle=\int g_1(x)g_2(x){\rm d}x $. 显然, 这个空间相比较于前两个例子比较小, 但是它与前面的两个例子有直接的关系, 有些性质是它们所不具有的. 定义:

$ \mathscr{H}_n(x)=(\sqrt{\pi}2^nn!)^{-1/2}H_n(x){\rm e}^{-x^2/2}, \quad n\ge 0, $

其中$ H_n(x) $是$ L^2(\mathbb{R}, \exp(-x^2)) $中的厄尔米特多项式, 则$ \{\mathscr{H}_n(x)\} $构成空间$ L^2(\mathbb{R}) $的标准正交基, 文献中称之为厄尔米特函数系. 更重要的是, 它是一致有界的,

$ \sup\limits_{x}\sup\limits_{n\ge 0}|\mathscr{H}_n(x)|\le \pi^{-1/4}, $

这一点对于计量模型估计量的极限理论是非常方便的.

例2.6  空间$ L^2(\mathbb{R}^+, {\rm e}^{-x}) $, $ \langle g_1, g_2\rangle=\int_0^{+\infty} g_1(x)g_2(x){\rm e}^{-x}{\rm d}x $. 拉盖尔多项式系(Laguerre polynomials)是其中的正交系, 具有Rodrigues表达式:

$ L_n(x)=\frac{{\rm e}^x}{n!}\frac{{\rm d}^n}{{\rm d}x^n}({\rm e}^{-x}x^n), \quad n\ge 0. $

另外, $ L_n(x) $满足微分方程$ xy''+(1-x)y'+ny=0 $和递推公式$ (n+1)L_{n+1}-(2n+1-x)L_n+nL_{n-1}=0 $, 其生成函数为:

$ \frac{1}{1-t}\exp\left(\frac{-xt}{1-t}\right)=\sum\limits_{n=0}^\infty L_n(x)t^n, $

而正交性为$ \langle L_n(x), L_m(x)\rangle=\delta_{nm} $.

例2.7  空间$ L^2(\mathbb{R}^+) $, $ \langle g_1, g_2\rangle = \int_0^{+\infty} g_1(x)g_2(x){\rm d}x $. 显然, 这个空间比前一个例子要小, 因为如果$ g(x)\in L^2(\mathbb{R}^+) $, 则$ g(x)\in L^2(\mathbb{R}^+, \exp(-x)) $. 另外, 类似于厄尔米特函数, 定义拉盖尔函数:

$ \mathscr{L}_n(x)=L_n(x){\rm e}^{-x/2}, \quad n\ge 0, $

则$ \{\mathscr{L}_n(x)\} $构成空间$ L^2(\mathbb{R}^+) $的标准正交基, 且具有有界性$ \sup_n\sup_x|\mathscr{L}_n(x)|\le 1 $.

例2.8  以下是两类常用的三角函数正交系: 1)傅里叶正交系. 令$ \varphi_0(x)=1, \varphi_{2j-1}(x)=\sin((2j-1)x), \varphi_{2j}(x)=\cos((2j-1)x) $, $ j=1, 2, \cdots $, 则$ \{\varphi_j(x), j\ge 0\} $是$ L^2[-\pi, \pi] $完备正交系; 2)余弦正交系. 令$ \varphi_0(x)=1, \varphi_j(x)=\sqrt{2}\cos(\pi j x), j\ge 1 $, 则$ \{\varphi_j(x), j\ge 0\} $是$ L^2[0, 1] $的标准正交基.

设$ \{\varphi_j(x), j\ge 0\} $是$ L^2([a, b], \rho(x)) $的一个正交基, 对于任意正整数$ k $, 记$ k $维向量函数$ Z_k(x) =(\varphi_0(x), \varphi_1(x), \cdots, \varphi_{k-1}(x))^\top $, 这里上标"$ \top $"表示向量或者矩阵的转置. 级数估计方法里常常包含着量$ \|Z_k(x)\|^2 $, 当$ k\to\infty $时, 它的大小很重要, 决定着级数估计量的收敛速度. 对于余弦正交系$ \{\varphi_j(x), j\ge 0\} $, Dong and Linton (2018)的引理A.4证明:

$ \begin{equation*} \frac{1}{k}\|Z_k(x)\|^2=1+O(1/k), \quad k\to\infty. \end{equation*} $

这意味着$ \|Z_k(x)\|^2\sim k $对$ x\in [0, 1] $一致成立.

当$ \{\varphi_j(x), j\ge 0\} $是$ L^2([-1, 1], \rho(x)) $($ \rho(x)>0 $)的标准正交多项式系, Lubinsky $ (2009, {\rm p}917) $的推论1.3证明:

$ \begin{equation*} \lim\limits_{ k\to\infty} \frac{1}{k}\|Z_k(x)\|^2=\frac{1}{\pi \rho(x) \sqrt{1-x^2}}, \quad x\in (-1, 1). \end{equation*} $

当$ \rho(x)=(b-x)^\beta(x-a)^\alpha $, $ \alpha, \beta\ge 0 $, $ \varphi_j(x) $是$ L^2([a, b], \rho(x)) $正交多项式系, Andrews $ (1991, {\rm p}326) $给出$ \max_{x\in[a, b]}\|Z_k(x)\|^2=O(k^{1+2\max(\alpha, \beta)}) $.

当$ \{\varphi_j(x), j\ge 0\} $是$ L^2(\mathbb{R}, {\rm e}^{-x^2}) $中的厄尔米特正交多项式系, Levin and Lubinsky (1992)中定理1.1证明:

$ \begin{equation*} \frac{1}{\sqrt{k}}\|Z_k(x)\|^2\asymp \exp (x^{2})\left(\max \left\{ k^{-2/3}, 1-\frac{|x|}{\sqrt{2k}}\right\}\right) ^{1/2}, \end{equation*} $

对于$ k\geq 1 $和$ x\in \{u:\ |u|\leq \sqrt{2k_{3}}(1+Lk^{-2/3})\} $一致成立, 这里$ L>0 $是一个常数.

级数估计的另一类重要问题是正交级数展开(1)的收敛性和收敛速度, 即, 除了按模收敛这个无穷级数是逐点收敛吗? 是一致收敛吗? 如果收敛, 其速度如何? 这些都是关系到筛分法使用的重要问题.

在$ L^2(\mathbb{R}) $中, Dong, Gao and Tjøstheim (2016)引理C.1研究了厄尔米特函数正交级数展开的逐点收敛和一致收敛的速度, 这个结果也可以用于$ L^2(\mathbb{R}, {\rm e}^{-x^2}) $无穷级数的逐点收敛; Dong, Linton and Peng (2021)引理A.5给出了空间$ L^2[-1, 1] $和$ L^2[0, 1] $中正交级数展开的一致收敛性和收敛速度, 这个结果可以用于任何有界区间上正交级数展开的收敛性.

级数估计里是否使用正交函数系也很重要. 可能有些读者认为没有必要在非参数问题里, 比如回归$ y=g(x)+e $, 使用正交多项式系来逼近$ g(x) $; 他们认为, 使用$ P_k(x)=(1, x, \cdots, x^{k-1})^\top $的线性组合或者使用$ g(x) $的泰勒级数在某点展开就可以了. 事实上, White (1980)指出泰勒级数展开式是极不恰当的, 它的最小二乘法估计量不会收敛到泰勒级数的系数. 另一方面, 对于观测值$ \{x_i, i=1, \cdots, n\} $, 当$ k $较大时回归矩阵$ \sum_{i=1}^nP_k(x_i)P_k(x_i)^\top $往往是病态的, 接近奇异; 这是因为$ x_i^j $的矩随着$ j $的变化差异很大, 而它们之间又具有很强的相关性. 所以, 从计算的角度考虑人们应该采用正交多项式系来降低这种异质性和相关性, 正如经典筛分法文章Andrews (1991, p325), Newey (1997, p156)所建议的那样.

这里讲的筛分法在无穷区间上的应用的主要动机是非平稳时间序列, 这样的变量是发散的, 不会囿于任何紧区间, 所以采用无穷区间上的正交系对非参数函数进行逼近是恰当的.

非线性非平稳时间序列模型在过去二十年里得到广泛关注和大量研究, 参见Park and Phillips(1999, 2001), Karlsen and Tjøstheim (2001), Karlsen, Mykelbust and Tjøstheim (2007), Wang and Phillips(2009a, 2009b, 2012), Gao, King and Lu et al. (2009a, 2009b), Gao and Phillips (2013), Dong, Gao and Tjøstheim (2016), Dong, Gao and Tjøstheim et al. (2017), Dong and Gao(2018, 2019), Dong and Linton (2018), Wang, Wu and Zhu (2018), Dong, Gao and Peng (2019), Dong, Linton and Peng (2021)等等. 这些理论也被应用于面板数据模型和实证分析, 比如Dong, Gao and Peng (2020)和朱平芳等(2020). 这种问题在理论上和实证上被广泛关注是因为非平稳时间序列大量地存在于经济, 金融和相关领域, 并且非线性非参数模型具有极强的灵活性, 从而得到应用者的青睐.

考虑部分线性单指标模型(partially linear single-index model):

(2) $ \begin{equation} y_t=\beta_0^\top x_t+g(\theta_0^\top x_t)+e_t, \quad t=1, \cdots, n, \end{equation} $

这里$ y_t $是被解释变量, 未知函数$ g(\cdot): \mathbb{R}\mapsto \mathbb{R} $是所谓的关联函数(link function), 假设它在$ \mathbb{R} $上可积, $ \beta_0 $和$ \theta_0 $是未知的$ d $维参数向量, $ x_t $是$ d $维单整过程(其严格定义随后给出), $ e_t $是误差过程, $ n $为样本容量. 对于$ \theta_0 $, 我们采用常见的识别性条件$ \|\theta_0\|=1 $, 且第一个分量为正.

众所周知, 纯粹的非参数模型在变量的维数较大时($ d>3 $)往往受到"维数魔咒"的制约不能正常工作, 模型(2)是一种降维的办法, 克服了"维数魔咒", 同时, 它还扩展了线性模型, 避免了可能的模型误设. 鉴于此, 模型(2) 被认为是纯粹的线性参数模型和纯粹的非参数模型的一种折中. 见Carroll et al. (1997), Xia and Li (1999), Xia et al. (2002), Yu and Ruppert (2002), Zhu and Xue (2006), Liang et al. (2010), Wang et al. (2010), Ma and Zhu (2013). 这些文章研究的变量都是平稳变量, 而我们这里考虑的是单位根向量过程, 这非常具有挑战性; 另外, 因为Gao and Phillips (2013)指出核方法在这种情形下可能不工作, 我们考虑使用筛分法, 这将带来另一种挑战, 即在无穷区间上使用筛分法.

当$ \beta_0=0 $时模型(2) 变成了单指标模型:

(3) $ \begin{equation} y_t=g(\theta_0^\top x_t)+e_t, \quad t=1, \cdots, n, \end{equation} $

而这个模型在$ x_t $为平稳变量时已经有很多研究了, 见Härdle, Hall and Ichimura (1993), Xia and Li (1999), Wu, Yu and Yu (2010). 我们将首先考虑模型(3), 然后研究模型(2).

估计步骤和模型假设  因为$ g(\cdot)\in L^2(\mathbb{R}) $, $ \{\mathscr{H}_i(x)\} $是该空间的标准正交基, 我们有无穷级数展开:

(4) $ \begin{equation} g(x)=\sum\limits_{i=0}^\infty c_i\mathscr{H}_i(x), \ \ \ \mbox{其中} \ \ \ c_i=\int g(x)\mathscr{H}_i(x){\rm d}x. \end{equation} $

取任意正整数$ k $, 定义部分和$ g_k(x)=\sum_{i=0}^{k-1}c_{i}\mathscr{H}_i(x) $, 及截断误差$ \gamma_k(x)=\sum_{i=k}^{\infty} c_i\mathscr{H}_i(x) $. 记$ Z_k^\top(\cdot) = (\mathscr{H}_0(\cdot), \cdots, \mathscr{H}_{k-1} (\cdot)) $, $ c^\top=(c_0, \cdots, c_{k-1}) $, 把模型(3)重写为:

$ \begin{align*} y_t=Z_k^\top(\theta^\top_0 x_t) c+\gamma_k(\theta^\top_0 x_t)+e_t, \ \ \ t=1, \cdots, n. \end{align*} $

进一步, 记向量$ Y=(y_1, \cdots, y_n)^\top $, $ n\times k $矩阵$ Z=(Z_k(\theta^\top_0 x_1), \cdots, Z_k(\theta^\top_0 x_n))^\top $, $ n $维向量$ \gamma=(\gamma_k(\theta^\top_0 x_1), \cdots, \gamma_k (\theta^\top_0 x_n))^\top $和$ e=(e_1, \cdots, e_n)^\top $. 这样, 我们把模型(3) 写为矩阵形式$ Y=Zc+\gamma+e $; 于是, 由最小二乘法得, $ \widetilde{c}= \widetilde{c} (\theta_0)=(Z^\top Z)^{-1}Z^\top Y $; 注意, $ \theta_0 $未知, 我们只得到$ \widetilde{c} $关于$ \theta_0 $的函数形式. 要估计$ \theta_0 $, 对于任意$ \theta\in \Theta $, 定义$ L_n(\theta)= \frac{1}{2}\sum_{t=1}^n [y_t-Z_k^\top (\theta^\top x_t) \widetilde{c}(\theta)]^2 $. 那么,

(5) $ \begin{equation} \widehat{\theta}_n=\underset{ \theta\in \Theta} {\text{argmin}}\ L_n(\theta), \end{equation} $

就是$ \theta_0 $的估计量. 这个估计的步骤就是剖面法(profile method), 见Severini and Wong (1992), Liang et al. (2010).

一旦得到$ \widehat{\theta}_n $, 我们定义$ \widehat{g}_n(u) \equiv \widehat{g}_n(u; \widehat{\theta}_n)=Z_k(u)^\top \widehat{c} $, $ \forall \; u\in \mathbb{R} $, 其中$ \widehat{c}= \widetilde{c}(\widehat{\theta}_n) $, 为$ g(u) $的插入估计量(plug-in estimator). 另外, 鉴于识别性条件$ \|\theta_0\|=1 $, 我们定义$ \widehat{\theta}_{n, \text{emp}} =\|\widehat{\theta}_n\|^{-1} \widehat{\theta}_n $为$ \theta_0 $的最终估计量.

下面我们考虑部分线性单指标模型的估计方法. 由(4), 对于每个$ t $把(2)重写为:

$ \begin{align*} y_t-\beta^\top_0 x_t=Z_k(\theta^\top_0 x_t)^\top c+\gamma_k(\theta^\top_0 x_t)+e_t, \end{align*} $

其中$ Z_k(\cdot) $, $ c $和$ \gamma_k(\cdot) $都是以前定义过的.

记$ n\times d $矩阵$ X=(x_1, x_2, \cdots, x_n)^\top $, 而$ Y, Z, \gamma, e $仍保持原有含义. 于是, $ Y-X\beta_0=Zc+\gamma+ e $. 由最小二乘法得$ \widetilde{c}= \widetilde{c}(\beta_0, \theta_0)=(Z^\top Z)^{-1}Z^\top (Y-X\beta_0) $. 对于一般参数$ (\beta, \theta) $, 定义$ L_n(\beta, \theta)=\frac{1}{2} \sum_{t=1}^n [y_t-\beta^\top x_t-Z_k^\top (\theta^\top x_t) \widetilde{c}(\beta, \theta)]^2 $. 因此, $ (\beta_0, \theta_0) $的估计量定义为:

(6) $ \begin{equation} \begin{pmatrix} \widehat{\beta}_n \\ \widehat{\theta}_n\end{pmatrix}=\underset{ \theta\in \Theta, \beta} {\text{argmin}}\ L_n(\beta, \theta). \end{equation} $

同样的, $ g(u) $的插入估计量为$ \widehat{g}_n(u)\equiv \widehat{g}_n(u; \widehat{\beta}_n, \widehat{\theta}_n) =Z_k^\top(u)\widehat{c} $, 其中$ \widehat{c}= \widetilde{c}(\widehat{\beta}_n, \widehat{\theta}_n) $; 标准化估计量$ \widehat{\theta}_{n, \text{emp}}=\|\widehat{\theta}_n\|^{-1} \widehat{\theta}_n $满足识别性条件.

假设A.1

(a) 设$ \{\varepsilon_j, -\infty<j< \infty\} $为$ d $维独立同分布的连续型随机变量序列, $ E\varepsilon_1=0 $, $ E[\varepsilon_1 \varepsilon_1^\top] =\Omega>0 $, 并且对于某个$ p>2 $, $ E\|\varepsilon_1 \|^p <\infty $. 假设$ \int |E\exp(iu \varepsilon_1)| {\rm d}u <\infty $, 即$ \varepsilon_1 $的特征函数是可积的.

(b) 令$ x_t=x_{t-1}+v_t $, $ t\geq 1 $, $ x_0=O_P(1) $, 这里线性过程$ v_t=\sum_{j=0}^\infty \rho_j \varepsilon_{t-j} $, 而$ \{\rho_j\} $是方阵序列, 满足$ \rho_0=I_d $, $ \sum_{j=0}^\infty \|\rho_j\|<\infty $且$ \rho= \sum_{j=0}^\infty \rho_j $满秩.

(c) 存在$ \sigma $-域序列$ \mathcal{F}_{t} $使得$ (e_t, \mathcal{F}_{t}) $构成鞅差序列, 即对于任意$ t $, $ E(e_t|\mathcal{F}_{t-1}) =0 $依概率1成立(a.s.). 另外, $ E(e^2_t| \mathcal{F}_{t-1}) =\sigma^2_e $ a.s.和$ \mu_4:= \sup_{1\le t\le n} E(e_t^4| \mathcal{F}_{t-1})<\infty $ a.s. 都成立.

(d) $ x_{t} $对于$ \mathcal{F}_{t-1} $适应.

(e) 令$ V_n(r)=\frac{1}{\sqrt{n}}\sum_{i=1}^{[nr]}v_i $, $ U_n(r)=\frac{1}{\sqrt{n}} \sum_{i=1}^{[nr]} e_i $. 假设当$ n\to \infty $时, $ (U_n(r), V_n(r))\rightarrow_D (U(r), V(r)) $. 这里, $ (U(r), V(r)) $是$ (d+1) $维布朗运动.

注  矩阵的模$ \|\cdot\| $在本文中均采用Frobenius模(以下不再说明). 假设A.1是非平稳时间序列模型常用条件. 条件(a)和(b) 给出了单整过程协变量$ x_t $的定义, 生成它的线性过程$ v_t $是以独立同分布序列$ \{\varepsilon_j, -\infty<j< \infty\} $为基础变量组合而成; 条件(c), (d)和(e) 正是在经典文章如Park and Phillips (2000), Wang and Phillips(2009a, 2009b, 2012), Gao et al. (2009a, 2009b)所使用的条件. 假设里的$ \sigma $- 域$ \mathcal{F}_{t} $可取为$ \mathcal{F}_{t}=\sigma(\cdots, \varepsilon_{t}, \varepsilon_{t+1}; e_1, \cdots, e_t) $.

由Skorohod表示定理(Pollard (1984))知, 存在一个母概率空间(a richer probability space), 其中有一个随机向量$ (U^0_n(r), V_n^0(r)) $, 使得$ (U_n(r), V_n(r))=_D (U^0_n(r), V_n^0(r)) $, 且在$ [0, 1]^{d+1} $上一致地有$ (U^0_n(r), V_n^0(r))\to_{\rm a.s.} (U(r), V(r)) $成立. 为避免将$ (U_n(r), V_n(r)) $反复地嵌入母空间以得到依分布相等的向量$ (U^0_n(r), V_n^0(r)) $, 我们简单地置$ (U_n(r), V_n(r))= (U^0_n(r), V_n^0(r)) $, 而不是$ (U_n(r), V_n(r))=_D (U^0_n(r), V_n^0(r)) $.

由于下面的引理是建立在母概率空间上, 本节的所有理论结果都应该理解为母空间的结果, 这一点我们不再重复.

假设B.1

(a) 设$ g(x) $在$ \mathbb{R} $上可微, 且对于$ \ell=0, 1, \cdots, m $, $ m $为给定正整数, $ g^{(m-\ell)}(x)x^\ell \in L^2(\mathbb{R}) $.

(b) 取$ k=[a\cdot n^\kappa] $, 这里$ a>0 $, $ \kappa\in (0, 1/8) $, $ \kappa(m-3)\ge \frac{1}{2} $, $ m $为(a) 给定.

注  条件(a) 保证了截断误差在随后的极限定理推导中可忽略. 条件(b)虽然对于$ \kappa $的选取具有较强的限制性, 我们在实践中可以取$ \kappa\in [\frac{5}{44}, \frac{5}{41}] $, $ m=8 $. 较大的$ m $和较小的$ \kappa $使得关联函数的正交级数展开收敛较快, 而截断误差不会影响极限理论.

单指标模型的渐近理论  我们将使用Wooldridge (1994)的基本方法来推导$ \widehat{\theta}_n $ (由式(5)所定义)的极限分布. 令$ S_n(\theta)=\frac{\partial }{\partial \theta}L_n(\theta) $和$ J_n(\theta)= \frac{\partial^2 }{\partial \theta \partial \theta^\top} L_n(\theta) $分别为目标函数的一阶偏导数和二阶海塞矩阵. 由泰勒公式,

(7) $ \begin{equation} 0=S_n(\widehat{\theta}_n)=S_n(\theta_0)+J_n(\theta_n)(\widehat{\theta}_n -\theta_0), \end{equation} $

其中, $ \theta_n $为介于$ \widehat{\theta}_n $和$ \theta_0 $的某一点.

取矩阵$ Q_2 $, 使$ Q=(\theta_{0}, Q_2) $为正交矩阵. 这个正交矩阵$ Q $构成$ \mathbb{R}^d $的新坐标系, 在此坐标系下, $ \theta_0 $, $ x_t $和$ \theta $的坐标成为:

(8) $ \begin{eqnarray} &&\alpha_0:= Q^\top \theta_0=(\alpha_{10}, \alpha_{20}^\top)^\top, \ \text{且}\ \alpha_{10}=\|\theta_{0}\|^2=1, \alpha_{20}=Q_2^\top \theta_{0}=0, \\ &&z_t:=Q^\top x_t=(x_{1t}, x_{2t}^\top)^\top, \quad \text{这里}\ x_{1t}:=\theta_0^\top x_t, \ x_{2t}:=Q_2^\top x_t, \\ &&\alpha:=Q^\top \theta, \quad \forall\ \theta. \end{eqnarray} $

值得注意的是, 因为$ \theta_0 $未知, 坐标旋转在实践中是不需要也是不可行的, 它只是为了理论推导才引入的.

因此, 单指标模型可以重写为$ y_t=g(\theta_0^\top QQ^\top x_t)+e_t= g(\alpha_{0}^\top z_{t}) +e_t $. 同时, 由假设A.1和连续映射定理, 对于$ r\in [0, 1] $, 当$ n\to\infty $,

(9) $ \begin{equation} \frac{1}{\sqrt{n}}x_{1[nr]}\to_D V_1(r)=\theta_0^\top V(r), \ \text{和}\ \frac{1}{\sqrt{n}}x_{2[nr]} \to_DV_2(r)=Q_2^\top V(r). \end{equation} $

如果$ \widehat{\alpha}_n $是$ \alpha_0 $的非线性最小二乘法估计量, 那么$ \widehat{\alpha}_n =Q^\top \widehat{\theta}_n $, 并且关于$ \alpha $的一阶偏导数$ S_n(\alpha) $和海塞矩阵$ J_n(\alpha) $为$ S_n(\alpha)=Q^\top S_n(\theta) $和$ J_n(\alpha)=Q^\top J_n(\theta)Q $. 用$ Q^\top $左乘方程(7)得,

(10) $ \begin{equation} 0=S_n(\widehat{\alpha}_n)=S_n(\alpha_0)+J_n(\alpha_n)(\widehat{\alpha}_n -\alpha_0). \end{equation} $

下面的定理先给出$ S_n(\alpha_0) $和$ J_n(\alpha_0) $的极限分布, 在此基础上可得$ \widehat{\alpha}_n -\alpha_0 $的极限分布.

定理3.1  令$ D_n= \text{diag} (n^{1/4}, n^{3/4}I_{d-1}) $. 在假设A.1和B.1下, 当$ n\rightarrow \infty $时,

(11) $ \begin{equation} D_n^{-1}S_n(\alpha_0)\to_D R^{1/2}W(1)\quad\text{和}\quad D_n^{-1}J_n(\alpha_0)D_n^{-1}\to_P R, \end{equation} $

这里$ W(r) $是一个$ d $维布朗运动向量, 它与$ V(r) $独立, 而对称分块矩阵$ R=\left(\begin{smallmatrix} r_{11}&r_{12} \\r_{21}&r_{22} \end{smallmatrix}\right) $,

$ \begin{align*} r_{11}=& L_1(1, 0)\int s^2\dot{g}^2(s){\rm d}s, & r_{12}=&\int_0^1V_2^\top(r){\rm d}L_1(r, 0)\int s\dot{g}^2(s){\rm d}s, \\ r_{21}=& r_{12}^\top, & r_{22}=&\int_0^1V_2(r)V_2^\top(r){\rm d}L_1(r, 0)\int \dot{g}^2(s){\rm d}s, \end{align*} $

其中, $ V_1 $和$ V_2 $是由(9)定义的维数分别为$ 1 $和$ d-1 $的布朗运动, $ L_1(r, 0) $是布朗运动$ V_1(\cdot) $的局部时过程(local time process), 它表示$ V_1 $在时间段$ [0, r] $内于零点逗留的时间.

此外, $ \widehat{\alpha}_n $是$ \alpha_0 $的相合估计量, 且当$ n\to \infty $时,

(12) $ \begin{equation} D_n(\widehat{\alpha}_n- \alpha_0)\to_D R^{-1/2}W(1). \end{equation} $

本节的所有证明请参考Dong, Gao and Tjøstheim (2016). Revuz and Yor (2005)是介绍布朗运动局部时过程的经典著作, 读者可以从中了解更多内容. 鉴于$ D_n $的结构, 我们由(12) 可得,

(13) $ \begin{equation} n^{1/4}(\widehat{\alpha}_{1n}-1)\to_D {\bf{MN}}(0, \rho_{11}), \ \text{和} \ n^{3/4} \widehat{\alpha}_{2n} \to_D {\bf{MN}}(0, \rho_{22}), \end{equation} $

其中$ \widehat{\alpha}_{n}=(\widehat{\alpha}_{1n}, \widehat{\alpha}_{2n}^\top)^\top $, $ {\bf{MN}}(0, \Xi) $代表混合正态分布(mixed normal distribution), 意为其分布为正态, 但其协方差矩阵$ \Xi $是随机的, $ \rho_{11} $和$ \rho_{22} $是矩阵$ R^{-1}=\left(\begin{smallmatrix} \rho_{11}& \rho_{12} \\ \rho_{21}& \rho_{22} \end{smallmatrix}\right) $的对角块,

(14) $ \begin{equation} \rho_{11}=(r_{11}-r_{12}r^{-1}_{22}r_{21})^{-1}, \quad \text{和} \quad \rho_{22}=(r_{22}-r_{21}r_{11}^{-1}r_{12})^{-1}. \end{equation} $

因此, $ \widehat{\alpha}_{n} $的两个子分量具有不同的速度.

在坐标系$ Q $里, $ \theta_0 $是一个坐标轴, 式(13)意味着估计量$ \widehat{\theta}_n $具有二重收敛速度: 它在$ \theta_0 $上的坐标(即$ \widehat{\alpha}_{1n} $)收敛于1的速度是$ n^{-1/4} $, 而在其他坐标轴$ Q_2 $上的坐标(即$ \widehat{\alpha}_{2n} $)收敛于零的速度可以达到$ n^{-3/4} $. 这种差异是由于单位根过程$ \{x_t\} $的概率密度的支撑集以勒贝格测度方式在实数轴上发散(即$ x_t=O_P(\sqrt{t}) $), 而$ g $函数可积, 在自变量足够大时$ g(\theta_0^\top x)\approx 0 $. 所以, 只有$ \{x_t\} $中沿着$ \theta_0 $取值适中的变量才对$ g $的估计有贡献, 而在正交于$ \theta_0 $的方向则无此限制, 即使$ \{x_t\} $取值很大, 它们对估计都是有用的, 提高了估计的效率. 当然, 这种现象在一元非参数回归问题中看不到.

注意到$ \widehat{\theta}_{n, \text{emp}}= \|\widehat{\theta}_n\|^{-1} \widehat{\theta}_n $. 直觉上, $ \widehat{\theta}_{n, \text{emp}} $收敛速度可能比$ \widehat{\theta}_n $要快. 这可以从旋转后坐标系看出. 因为$ \widehat{\theta}_n=Q \widehat{\alpha }_{n} $, 所以$ \|\widehat{\theta}_n\|=\| \widehat{\alpha}_{n}\| $, $ \widehat{\theta}_{n, \text{emp}}= Q\widehat{\alpha}_{n, \text{unit}} $, 其中$ \widehat{\alpha}_{n, \text{unit}}= (\widehat{\alpha}_{n, \text{unit}}^1, (\widehat{\alpha}_{n, \text{unit}}^2)^\top)^\top=\|\widehat{\alpha}_{n}\|^{-1} \widehat{\alpha}_{n} $. 下面推论和定理分别给出了$ \widehat{\alpha}_{n, \text{unit}} $, $ \widehat{\theta}_{n} $和$ \widehat{\theta}_{n, \text{emp}} $收敛速度.

推论3.1  在假设A.1和B.1下, 当$ n\to \infty $时我们有:

$ \begin{equation*} n^{3/2} (\widehat{\alpha}_{n, \text{unit}}^1-1)\to_D -\frac{1}{2}\|\xi\|^2\quad \text{和} \quad n^{3/4} \widehat{\alpha}_{n, \text{unit}}^2\to_D \xi, \end{equation*} $

这里$ \xi\sim {\bf{MN}}(0, \rho_{22}) $由式(13)定义.

注意, 经过标准化原来收敛较慢的速度提高到$ n^{-3/2} $, 而另一部分保持$ n^{-3/2} $的收敛速率. 同时, 虽然$ \widehat{\alpha}_{n, \text{unit}}^1\to_P 1 $, 但是$ \widehat{\alpha}_{n, \text{unit}}^1 =\|\widehat{\alpha}_{n} \|^{-1}\widehat{\alpha}_{1n}\le 1 $. 直觉上, $ \widehat{\alpha}_{n, \text{unit}}^1 $的速度变快的原因是它利用了与$ \theta_0 $正交方向上来自于$ x_t $的信息较为充分的缘故. 我们将采用蒙特卡罗试验验证这一点.

定理3.2  在假设A.1和B.1下, 当$ n\to \infty $时我们有:

(15) $ \begin{align} & n^{1/4} (\widehat{\theta}_n-\theta_0)\to_D {\bf{MN}}(0, \rho_{11} \theta_0 \theta_0^\top), \end{align} $

(16) $ \begin{align} & n^{3/4} (\widehat{\theta}_{n, \text{emp}}-\theta_0)\to_D {\bf{MN}}(0, Q_2 \rho_{22} Q_2^\top). \end{align} $

可以看到, $ \widehat{\theta}_n $以$ n^{-1/4} $的速度收敛到$ \theta_0 $, 而$ \widehat{\theta}_{n, \text{emp}} $以$ n^{-3/4} $的速度收敛于$ \theta_0 $. 标准化将$ \widehat{\theta}_{n} $的长度直接调整为1, 从而加快了收敛速度, 因为长度收敛到1慢于向量$ \widehat{\theta}_n $的角度与$ \theta_0 $重合的速度(见式(13)).

因为$ \widehat{\theta}_n\sim {\bf{MN}} (\theta_0, n^{-1/4} \rho_{11} \theta_0 \theta_0^\top) $, 我们证明$ \widehat{\theta}_n $的协方差矩阵是海塞矩阵的逆$ [J_n(\widehat{\theta}_n) ]^{-1} $或者$ [\widetilde{J}_n (\widehat{\theta}_n) ]^{-1} $, 其中$ \widetilde{J}_n(\theta)=\sum_{t=1}^n \dot{\widehat{g}}_n^2 (\theta^\top x_t)x_tx_t^\top $是$ J_n(\theta) $的主项. 同时, 定义$ \sigma_e $和$ L_1(1, 0) $的估计量:

(17) $ \begin{align} \widehat{\sigma}_e^2=\frac{1}{n}\sum\limits_{t=1}^n[y_t- \widehat{g}_n(\widehat{\theta}_n^\top x_t)]^2 \ \ \mbox{和} \ \ \widehat{L}_{n1}(1, 0)=\frac{1}{\sqrt{n}}\sum\limits_{t=1}^n \mathscr{H}_0^2 (\widehat{\theta}_n^\top x_t), \end{align} $

这里$ \mathscr{H}_0(\cdot) $是第一个厄尔米特函数.

推论3.2  在假设A.1和B.1下, 当$ n\to \infty $时我们有:

(18) $ \begin{equation} \widehat{\sigma}_e^2\to_P \sigma_e^2 \quad \text{和} \quad \widehat{L}_{n1}(1, 0)-L_1(1, 0)\to_P 0, \end{equation} $

并且,

(19) $ \begin{equation} \sqrt{n}[J_n(\widehat{\theta}_n)]^{-1} \to_P \rho_{11} \theta_0 \theta_0^\top \ \ \mbox{和}\ \ \sqrt{n}[\widetilde{J}_n (\widehat{\theta}_n) ]^{-1} \to_P \rho_{11} \theta_0 \theta_0^\top. \end{equation} $

我们下面为插入估计量$ \widehat{g}_n(u)=Z_k^\top (u)\widehat{c} $, $ u\in \mathbb{R} $, 建立中心极限定理.

定理3.3  在假设A.1和B.1下, 当$ n\to \infty $时我们有$ \sup_{u\in \mathbb{R}}|\widehat{g}_n(u)-g(u)|\to_P0 $, 并且,

(20) $ \begin{equation} \widehat{\sigma}_e^{-1}\widehat{L}_{n1}^{1/2}(1, 0)n^{1/4} \|Z_k(u)\|^{-1}(\widehat{g}_n(u)-g(u))\to_DN(0, 1). \end{equation} $

因为$ \|Z_k(u)\|^2= O(\sqrt{k}) $, 这里的收敛阶为$ O_P((n/k)^{1/4}) $, 这与核估计的结果类似. Wang and Phillips (2009a, p721)中定理3.1证明, 对于一元非参数回归$ y_t=f(x_t)+u_t $, $ \hat{f}(x)-f(x) $与$ \left(h\sum_{t=1}^n K_h(x_t-x) \right)^{-1/2} $同阶, 这里$ h $是窗宽, $ K_h(\cdot)=K(\cdot /h)/h $是核函数, $ \hat{f}(x) $是$ f(x) $的核估计, 而$ \left(h\sum_{t=1}^n K_h(x_t-x)\right)^{1/2}=O_P(1)n^{1/4}h^{1/2} $. 至此, 单指标模型的极限理论都已建立.

部分线性单指标模型的渐近理论  记$ \vartheta_0 =(\beta_0^\top, \theta_0^\top)^\top $, 用$ \vartheta=(\beta^\top, \theta^\top)^\top $表示一般参数. 令$ \mathfrak{S}_n(\vartheta) $和$ \mathfrak{J}_n(\vartheta) $分别为最小化问题(6)里目标函数$ L_n(\vartheta) $的一阶偏导数向量和二阶海塞矩阵. 令$ \widehat{\vartheta}_n $为$ \vartheta_0 $的估计量. 我们有:

(21) $ \begin{equation} 0=\mathfrak{S}_n(\widehat{\vartheta}_n)= \mathfrak{S}_n(\vartheta_0)+ \mathfrak{J}_n(\vartheta_n)(\widehat{\vartheta}_n -\vartheta_0), \end{equation} $

其中$ \mathfrak{J}_n(\vartheta_n) $是海塞矩阵在连接$ \widehat{\vartheta}_n $和$ \vartheta_0 $的线段上某一点$ \vartheta_n $处的值.

为推导模型(2)的极限理论, 我们也需要将坐标系进行旋转. 使用正交矩阵$ Q=(\theta_0, Q_2) $, 我们得到:

(22) $ \begin{align} y_t=\beta_0^\top QQ^\top x_t+g(\theta_0^\top QQ^\top x_t)+e_t=\lambda_{0}^\top z_{t}+ g(\alpha_{0}^\top z_{t})+e_t, \end{align} $

这里$ \lambda_0=Q^\top \beta_0=(\lambda_{10}, \lambda_{20}^\top)^\top $, $ \lambda_{10}=\theta_0^\top \beta_0 $是标量, $ \lambda_{20}=Q_2^\top \beta_0 $是$ (d-1) $维向量, 而$ \alpha_{0}=Q^\top \theta_0 $, $ z_{t}=Q^\top x_t $和以前一样. 令$ \lambda =Q^\top \beta $和$ \alpha =Q^\top\theta $是对一般向量的旋转, 且我们记$ \mu_0= (\lambda_0^\top, \alpha_0^\top)^\top $, $ \mu=(\lambda^\top, \alpha^\top)^\top $.

令$ L_n(\mu) $是坐标系旋转以后的目标函数(之前为$ L_n(\beta, \theta) $). 如果$ \widehat{\mu}_n $是$ \mu_0 $的估计量, 使$ L_n(\mu) $达到最小, 那么$ \widehat{\mu}_n =\text{diag} (Q^\top, Q^\top) \widehat{\vartheta}_n $. 另外, 一阶偏导向量$ \mathfrak{S}_n(\mu) $和二阶海塞矩阵$ \mathfrak{J}_n(\mu) $和旋转前的一阶偏导向量与二阶海塞矩阵有如下对应关系, $ \mathfrak{S}_n (\mu)=\text{diag}(Q^\top, Q^\top) \mathfrak{S}_n(\vartheta) $, $ \mathfrak{J}_n (\mu)=\text{diag}(Q^\top, Q^\top) \mathfrak{J}_n(\vartheta) \text{diag}(Q, Q) $.

用$ \text{diag}(Q^\top, Q^\top) $左乘方程(21)可得:

(23) $ \begin{equation} 0=\mathfrak{S}_n(\widehat{\mu}_n)=\mathfrak{S}_n(\mu_0) +\mathfrak{J}_n(\mu_n)(\widehat{\mu}_n -\mu_0), \end{equation} $

由此我们有下述定理.

定理3.4  在假设A.1和B.1下, 当$ n\to \infty $时我们有$ \widehat{\mu}_n\to_P\mu_0 $. 进而, 当$ n\rightarrow \infty $,

(24) $ \begin{eqnarray} && n(\widehat{\lambda}_n-\lambda_0)\to_D Q^\top \left(\int_0^1V(r) V^\top(r){\rm d}r \right)^{-1} \int_0^1V(r){\rm d}U(r), \end{eqnarray} $

(25) $ \begin{eqnarray} && D_n(\widehat{\alpha}_n-\alpha_0)\to_D R^{-1/2}W(1), \end{eqnarray} $

其中$ (U(r), V(r)) $在假设A.1定义, 而$ D_n $, $ R $和$ W $均保持它们在定理3.1里的意义.

定理3.4表明在部分线性单指标模型中, 线性部分参数的估计量具有线性模型参数估计量的收敛速度($ n^{-1} $, 线性协整回归所具有的超速度(super rate)), 但是指标向量的估计量在$ Q $坐标系下仍然具有双重收敛速度. 由此, 我们可以说部分线性单指标模型拥有三重收敛速度. 从定理3.4我们可以得到$ \widehat{\beta}_n $和$ \widehat{\theta}_n $的渐近分布.

定理3.5  在假设A.1和B.1下, 对于由式(6)所定义的($ \widehat{\beta}_n $, $ \widehat{\theta}_n $), 当$ n\rightarrow \infty $,

(26) $ \begin{eqnarray} && n(\widehat{\beta}_n-\beta_0)\to_D\left(\int_0^1V(r)V^\top(r){\rm d}r\right)^{-1} \int_0^1V(r){\rm d}U(r), \end{eqnarray} $

(27) $ \begin{eqnarray} && n^{1/4}(\widehat{\theta}_n-\theta_0)\to_D{\bf MN}(0, \rho_{11}\theta_0 \theta_0^\top). \end{eqnarray} $

定理3.6  在假设A.1和B.1下, 定理3.2$ \sim $3.3和推论3.1$ \sim $3.2中的所有结论对于模型(2)的$ \widehat{\theta}_n $和$ \widehat{g}_n(u) $都成立.

蒙特卡罗模拟实验  令$ d=2 $, $ x_t $由下列程序生成:

(28) $ \begin{equation} x_t=x_{t-1}+v_t \ \ \mbox{其中} \ \ v_t=r_0v_{t-1}+\varepsilon_t, \end{equation} $

$ t=1, \cdots, n $, 这里$ r_0=0.1 $, $ \varepsilon_t\sim iiN(0, \sigma^2 I_2) $, $ x_0=0 $. 取样本容量$ n=400, 600 $和$ 1000 $, 蒙特卡罗实验重复次数为$ M=2000 $. 截断参数$ k=[a\cdot n^{\kappa}] $, $ \kappa=\frac{5}{44} $, $ a=3.65 $, 满足假设B.1.

例3.1  考虑单指标模型$ y_t= g(\theta_0^\top x_t)+ e_t $, $ e_t\sim N(0, 1) $, $ t=1, \cdots, n $. 这个实验包括两种情况, I: $ \theta_0^\top= (0.6, -0.8) $和II: $ \theta_0^\top=(1, 0) $, 均满足$ \|\theta_0\|=1 $.

我们将计算估计量$ \widehat{\theta}_n= (\widehat{\theta}_{1n}, \widehat{\theta}_{2n})^\top $估计偏误和标准差:

(29) $ \begin{align} \text{Bias}=&\bar{\widehat{\theta}}_n -\theta_0, & \text{s.d.}=&\left(\frac{1}{M} \sum\limits_{\ell=1}^M (\widehat{\theta}_{n\ell} -\bar{\widehat{\theta}}_n)^{\otimes 2}\right)^{\otimes 1/2}, \end{align} $

这里$ \otimes $代表元素层面的运算, $ \bar{\widehat{\theta}}_n= \frac{1}{M} \sum_{\ell=1}^M \widehat{\theta}_{n\ell} $, 而$ \widehat{\theta}_{n\ell} $代表第$ \ell $次蒙特卡罗估计结果. 为了检验定理3.2的极限理论, 我们也计算了$ \widehat{\theta}_{n, \text{emp}} =\widehat{\theta}_n/\| \widehat{\theta}_n \| $的偏误和标准差.

Part I. 取$ \theta_0^\top= (0.6, 0.8) $, $ \sigma=0.6 $, $ g(u)= (1+u^2) {\rm e}^{-u^2} $. 我们估计$ \theta_0 $, 得到下面结果, 表 1.

可以看到, $ \widehat{\theta}_n $的偏误和标准差都随着样本容量的增大而减小, 并且$ \widehat{\theta}_{1n} $和$ \widehat{\theta}_{2n} $有相似的表现. 此外, 从偏误和标准差看, $ \widehat{\theta}_{n, \text{emp}} $的收敛速度较$ \widehat{\theta}_n $为快, 支持了定理3.2.

Part II. 令$ \theta_0^\top= (1, 0) $, $ \sigma=0.6 $, $ g(u)=(1+u^2)\exp(-u^2) $. 我们曾指出, 坐标系的旋转仅仅是为了渐近理论的推导. 为了检验定理3.1, 我们直接取$ \theta_0^{\top}=\alpha_0^{\top} =(1, 0) $, 从而$ \widehat{\alpha}_n =\widehat{\theta}_n $. 模拟结果见表 2.

从报告的结果来看, $ \widehat{\alpha}_{1n} $和$ \widehat{\alpha}_{2n} $的偏误与标准差都随着样本容量的增加而减小, 尤其是, 这种减少对于$ \widehat{\alpha}_{2n} $要远远快于$ \widehat{\alpha}_{1n} $. 这和定理3.1的理论结果$ \widehat{\alpha}_{2n}- \alpha_{20}=O_P(n^{-3/4}) $, $ \widehat{\alpha}_{1n}- \alpha_{10}= O_P(n^{-1/4}) $相一致.

然而, 从标准差来看, $ \widehat{\alpha}_{n, \text{unit}}^1 $的收敛明显比$ \widehat{\alpha}_{n, \text{unit}}^2 $快, 这与推论3.1的结果$ \widehat{\alpha}_{n, \text{unit}}^1-\alpha_{10}=O_P(n^{-3/2}) $和$ \widehat{\alpha}_{n, \text{unit}}^2 -\alpha_{20}=O_P(n^{-3/4}) $相一致. 我们也注意到$ \widehat{\alpha}_{n, \text{unit}}^1 $的偏误总是负的(由定义, $ \widehat{\alpha}_{n, \text{unit}}^1\le \alpha_{10}=1 $). 因此, $ \widehat{\alpha}_{n, \text{unit}}^1 $的偏误趋于零相对于$ \widehat{\alpha}_{n, \text{unit}}^2 $的偏误慢. 另外, $ \widehat{\alpha}_{n, \text{unit}}^2 $和$ \widehat{\alpha}_{2n} $的表现类似, 因为理论上它们有相同的阶.

例3.2  考虑部分线性单指标模型$ y_t= \beta_0^\top x_t+g(\theta_0^\top x_t)+ e_t $, $ e_t\sim N(0, 1) $, $ t=1, \cdots, n $, $ g(u)=(1+u^2) \exp(-u^2) $, $ \beta_0^\top=(0.3, 0.5) $, $ \theta_0^\top=(0.6, -0.8) $, 而$ \varepsilon_t \sim iiN(0, \sigma^2 \ I_2) $, $ \sigma=0.8 $.

表 3报告了所有计算结果. 从报表中看到, 所有估计量的偏误和标准差都随着样本容量的增大而减小; $ \widehat{\theta}_{n, \text{emp}} $趋于真值的速度看起来比$ \widehat{\theta}_n $快. 这是由于定理3.5$ \sim $3.6的理论结果$ \widehat{\theta}_n- \theta_0=O_P(n^{-1/4}) $和$ \widehat{\theta}_{n, \text{emp}} -\theta_0=O_P(n^{-3/4}) $. 同时, 在定理3.5中$ \widehat{\beta}_n= (\widehat{\beta}_{1n}, \widehat{\beta}_{2n})^\top $具有超级收敛速度$ n^{-1} $, 这在实验中由$ \widehat{\beta}_n $的偏误和标准差得到验证. 因此, 前面所建立的极限定理在蒙特卡罗实验里得到印证.

关于本节研究的识别性检验, 相关的文献包括Hong et al. (1995), Gao et al. (2009a, 2009b), Hong and Phillips (2010), Wang and Phillips (2012). 其中, Hong and White (1995)在对立假设下考虑了非参数函数的傅里叶级数逼近和样条逼近; Gao et al. (2009b)提出了一种基于非参数核方法的检验, 所针对的模型的回归变量是单整的, 与误差项独立, 而误差项是一个鞅差过程; Gao et al. (2009a)考虑了非平稳非线性自回归模型的检验, 但是对于误差项的密度函数要求苛刻; Hong and Phillips (2010)在实证问题中检验了协整关系的线性性; 而Wang and Phillips (2012)所考察的非平稳非线性回归模型检验则要求回归函数具有一定的增长速度, 比如多项式和幂函数等.

因此, 文献里的研究存在一个空白, 那就是对于可积函数缺乏识别性检验的研究(Wang and Phillips (2012, p731)); 同时, 文献里的研究都不涉及内生性问题, 这对实证研究非常重要. 所以, 我们的研究旨在对可积非平稳内生性模型提出识别性检验统计量, 并允许两种形式的内生性存在. 通常, 解决内生性需要工具变量, 我们在不需要工具变量情形下证明, 原假设下的统计量具有已知的分布, 对立假设下统计量则发散.

注意到, Wang and Phillips (2016)将Dong et al. (2017)的工作论文(2014年)提出的基于核估计方法的统计量扩展到基于内生性的模型. 然而正如Dong et al. (2017)所指出, 这种统计量的表现取决于一个任意选择的权函数. 相反, 我们提出的统计量非常简单且容易使用; 我们的统计量可以识别任意"微小"的局部偏离, 这里"微小"偏离是指趋于零的可积函数, 具体要求见假设C.2.

考虑非参数协整模型:

(30) $ \begin{align} y_t=&m(x_t)+e_t, \\ x_t=&D^{-\alpha_0} \{u_tI(t> 0)\}, \\ E[u_t]& =E[e_t]=0, \end{align} $

$ t=1, \cdots, n $, 这里函数$ m(\cdot) $未知, $ x_t $是分数阶单整非平稳过程, $ D $为差分算子, $ \alpha_0\in(1/2, 3/2) $, $ u_t $和$ e_t $互为内生(见下面假设A.2).

我们要检验下列假设:

(31) $ \begin{equation} H_0: \ \ m(x)=g(x;\theta_0)\ \ \ \mbox{v.s.} \ \ \ H_1: \ \ m(x)=g(x;\theta_1) +\Delta_{n}(x), \end{equation} $

其中$ g(x; \cdot) $已知, 在$ \mathbb{R} $上可积, $ \theta_0, \theta_1\in \Theta $, $ \Theta\subset \mathbb{R}^d $是紧参数空间, 而$ \{\Delta_{n}(x)\} $是一列未知函数, 满足$ \lim\limits _{n\to\infty} \Delta_{n}(x)=0 $对任意$ x\in\mathbb{R} $成立. 这里我们研究的是一种局部对立假设$ H_1 $, 类似于Wang and Phillips $ (2012, {\rm p}732) $, 因为一个固定不变的对立假设并没有多大意义(参考Horowitz and Spokiony (2001)).

为了拓宽研究范围, 我们允许模型(30)具有两种类型的内生性: 类型(i), 线性过程$ u_t=\sum_{j=0}^\infty \psi_j \epsilon_{t-j} $和$ e_t=\sum_{j=0}^\infty \phi_j \epsilon_{t-j} $由同一个独立同分布序列$ \{\epsilon_i: -\infty<i<\infty\} $生成; 类型(ii), $ u_t=\sum_{j=0}^\infty \psi_j \epsilon_{t-j} $是线性过程, 而$ e_t=\wp(\epsilon_t, \cdots, \epsilon_{t-m_0+1}; \eta_t, \cdots \eta_{t-m_1+1}) $是一个函数, 且$ \epsilon_i $和$ \eta_j $独立. 取决于线性过程的系数和函数的形式, 这样的设定包含了许许多多$ e_t $和$ u_t $的可能性. 两个极端的例子是(a) $ e_t=u_t $和(b) $ e_t $和$ u_t $互相独立. 同时, 这里提出的对于非平稳性和内生性模型的识别性检验在文献里是有开创性的, 极大地方便了识别性检验方法和理论在实际问题的使用.

在原假设下$ m(x)\in L^2(\mathbb{R}) $. 我们所提出的检验统计量大致上度量了误差$ y_t- g(x_t; \widehat{\theta}) $在空间$ L^2(\mathbb{R}) $的加权距离, 而权函数由空间的正交基构成, 这里$ \widehat{\theta} $是在原假设$ H_0 $下$ \theta_0 $的相合估计. 随后, 这种方法拓展到函数空间$ L^2(\mathbb{R}, {\rm e}^{-x^2}) $. 这主要是利用了变换$ M(x) = m(x)\exp(-x^2/2) $, 虽然$ m(x) $可能不可积, 但是$ M(x) $在$ \mathbb{R} $可积. 因此, 函数$ m(x) $所属的类得到极大丰富, 它可以是任何有界函数, 多项式和幂函数, 从而包括了已有文献Gao et al. (2009b), Wang and Phillips (2012, 2016), 并且填补了文献里的空白.

模型假设  设$ L $是滞后算子, $ D=1-L $是通常的差分算子. 分数阶差分算子$ D^{-\zeta}=(1-L)^{-\zeta} $由无穷级数$ D^{-\zeta}=\sum_{j=0}^\infty a_j(\zeta) L^j $定义, 这里$ a_j(\zeta)=\frac{\Gamma(j+\zeta)}{ \Gamma(\zeta) \Gamma(j+1)} $, $ \Gamma(\cdot) $是通常的伽马函数.

令$ \{\epsilon_j, j\in \mathbb{Z}\} $是独立同分布序列, $ \epsilon_0 $是连续型随机变量, 满足$ E[\epsilon_0]=0 $, $ E[\epsilon_0^2]=1 $和$ E[\epsilon_0^4]<\infty $. 进一步假设$ \epsilon_0 $的特征函数满足$ \int |u\, E {\rm e}^{iu\epsilon_0}| {\rm d}u <\infty $.

假设A.2

(a) 设$ x_t=D^{-\alpha_0} \{u_tI(t> 0)\} $, $ t\ge 1 $, $ x_0=O_P(1) $, $ \alpha_0\in (1/2, 3/2) $.

(b) 假设$ \{u_t\} $是线性过程, $ u_t=\Psi(L; \rho_0) \epsilon_{t}= \sum_{j=0}^\infty \psi_j(\rho_0) \epsilon_{t-j} $, 这里$ \rho_0\in \Xi $是$ p $维未知向量, $ \Xi $是紧集, $ \Psi(s; \rho)= \sum_{j=0}^\infty \psi_j(\rho)s^j $, $ \psi_0(\rho)\equiv 1 $, $ \Psi(s; \rho) $关于$ s $连续, $ (s; \rho)\in\mathbb{C}\times \mathbb{R}^p $, $ \psi:=\Psi(1; \rho_0)= \sum_{j=0}^\infty \psi_j(\rho_0)\ne 0 $. 另外, $ \Psi(s; \rho) $满足:

(ⅰ) 对于所有$ \rho\ne \rho_0 $, $ \rho\in \Xi\subset \mathbb{R}^p $, 我们有$ |\Psi(s; \rho)|\ne |\Psi(s; \rho_0)| $在任何具有正勒贝格测度的集合$ S\subset \{s: |s|=1\} $上成立.

(ⅱ) 对于所有$ \rho $, $ \Psi({\rm e}^{i\nu}; \rho) $关于$ \nu\in \mathbb{R} $可微, 且其导数属于Lip($ \varsigma $), $ \varsigma>1/2 $, 即, $ |U(\nu_1; \rho)-U(\nu_2; \rho)|\le c(\rho) |\nu_1- \nu_2|^\varsigma $对任何$ \nu_1, \nu_2\in \mathbb{R} $成立, 这里$ U(\nu;\rho)=\partial \Psi({\rm e}^{i\nu}; \rho)/\partial \nu $.

(ⅲ) 对于所有$ \nu\in \mathbb{R} $, $ \Psi({\rm e}^{i\nu}; \rho) $关于$ \rho $连续.

(ⅳ) 对所有$ \rho\in \Xi $, $ |\Psi(s; \rho)|\ne 0 $, $ |s|\le 1 $.

(c) 误差项序列$ \{e_t\} $满足

(ⅰ) $ e_t=\sum_{j=0}^\infty \phi_j \epsilon_{t-j} $, 其中$ \phi_0=1 $, 对于某个$ \gamma_0>3/2 $, 极限$ \lim\limits_{j\to \infty} \phi_j j^{\gamma_0} $存在, 记$ \phi:= \sum_{j=0}^\infty \phi_j\neq 0 $; 或者

(ⅱ) $ e_t=\wp(\epsilon_t, \cdots, \epsilon_{t-m_0+1}; \eta_t, \cdots, \eta_{t-m_1+1}) $这里$ \min(m_0, m_1)\ge 1 $, $ \{\eta_t\} $是i.i.d.$ (0, 1) $连续变量序列, 独立于$ \{\epsilon_t\} $, 函数$ \wp(\cdots) $是$ \mathbb{R}^{m_0+m_1} \mapsto \mathbb{R} $可测映射, $ E[e_t]=0 $, $ E[e_t^4]<\infty $对$ t> \max(m_0, m_1) $成立; 当$ t\le\max(m_0, m_1) $, 令$ e_t=0 $.

这个假设给出了模型(30)的协变量和均衡误差的结构, 它们均以$ \epsilon_j $和$ \eta_j $为基石而生成. 其中, $ x_t $是由$ u_t $分数阶单整而成, 而$ u_t $和$ e_t $是由i.i.d.(0, $ \sigma^2 $)序列$ \{\epsilon_j\} $生成. 取决于线性过程的系数和函数$ \wp $的选择, 这种设定给模型以最大的可能性包含内生性和外生性. 例如, 若$ \phi_j=\psi_j $对每个$ j $成立, 那么$ e_t=u_t $, 模型蕴含最高的内生程度; 若函数$ \wp $不包括任何$ \epsilon_j $, 则$ e_t $与$ u_s $独立, 从而与$ x_t $独立, 这就导致了外生性.

注意, $ x_t $是由一个被截断的无穷级数所定义, $ x_t=\sum_{\ell=0}^{t-1} a_\ell(\alpha_0) u_{t-\ell} $这里$ a_\ell(\alpha_0)= \Gamma(\ell+\alpha_0)/[\Gamma(\alpha_0) \Gamma(\ell+1)] $. 如果不截断, $ x_t $的二阶矩就不存在. 注意, 当$ \alpha_0\in (1/2, 3/2) $时$ x_t $是非平稳的, 尤其是如果$ \alpha_0=1 $, $ x_t $就是一个单位根过程.

当$ n\to \infty $, 可以证明$ d_n^2:=E[x_n^2] \sim \psi^2\Gamma^{-2} (\alpha_0) n^{2\alpha_0-1} (1+o(1)) $. 定义$ D[0, 1] $为$ [0, 1] $上的思科罗霍德空间(Skorokhod space), 即所有定义于$ [0, 1] $上每一点都右连续且左极限存在的函数集合. 根据Marinocci and Robinson (2000), 对$ r\in [0, 1] $, 在空间$ D[0, 1] $,

(32) $ \begin{equation} x_{n[nr]}:=\frac{1}{d_n}x_{[nr]}\to_D W(r;\alpha_0):=\int_0^r (r-s)^{\alpha_0-1}{\rm d}B(s). \end{equation} $

这里$ [\cdot] $代表最大整数部分, $ W(r;\alpha_0) $是由标准布朗运动$ B(s) $所定义的第二类型的分数阶布朗运动(Type II fractional Brownian motion). 另外, 随机过程$ W(r;\alpha_0) $具有连续的局部时过程$ L_W(t, a) $, 它代表$ W(r;\alpha_0) $在时段$ [0, t] $上于空间$ a $点逗留的时间. 要了解更多关于$ W(r;\alpha_0) $的信息, 请参考Marinucci and Robinson (2000).

由第二节知, 厄尔米特函数$ \{\mathscr{H}_i(x)\} $是空间$ L^2(\mathbb{R}) $的标准正交基, 对于任意$ g(x)\in L^2(\mathbb{R}) $, 我们有正交级数展开$ g(x) = \sum_{i=0}^\infty \beta_{i} \mathscr{H}_i(x) $, $ \beta_{i}=\int g(x) \mathscr{H}_i(x){\rm d}x $. 设$ k $为正整数, 定义部分和$ g_k(x)=\sum_{i=0}^{k-1} \beta_{i} \mathscr{H}_i(x) $. 那么, 当$ k\to\infty $, $ g_k(x)\to g(x) $在$ L^2 $意义下成立.

假设B.2

(a) 令$ k=[c\cdot n^{\kappa}] $, 这里$ \kappa $满足$ \max(0, 2(1-\alpha_0))<\kappa <\frac{3}{2}-\alpha_0 $, $ c>0 $为常数.

(b) 在$ H_0 $下, 存在$ \theta_0 $的相合估计量$ \widehat{\theta} $, 使得$ P(\|\widehat{\theta}- \theta_0\|> M \zeta_n)<\varepsilon_0 $对任意$ \varepsilon_0>0 $和某个$ M=M(\varepsilon_0) $成立, 这里$ \zeta_n\sqrt{\frac{n}{kd_n}}=O(1) $. 如果把$ \theta_0 $换成$ \theta_1 $, 此结论在$ H_1 $下也成立.

(c) 假设$ g(x;\theta) $关于$ \theta $二次可微, 对每个固定的$ \theta \in \Theta $, $ g(x;\theta)\in L^2(\mathbb{R}) $. 记$ l_1(x, \theta):= \frac{\partial}{ \partial \theta} g(x;\theta) $和$ l_2(x, \theta):= \frac{\partial^2} { \partial \theta \partial \theta^\top} g(x;\theta) $. 进一步假设$ \|l_1(x, \cdot)\|, \|l_2(x, \cdot)\|\in L^1(\mathbb{R}) \cap L^2(\mathbb{R}) $, 且存在一个正函数$ l(x)\in L^1(\mathbb{R}) \cap L^2(\mathbb{R}) $使得$ \|l_2(x, \cdot)\|\le l(x) $.

注  条件(a)对于截断参数$ k $要求, 当$ n\to \infty $时$ k\to \infty $但是用$ \kappa $限制它的速度. 此外, $ \kappa $也受到分数阶差分$ \alpha_0 $限制, 需要满足$ n/(kd_n)\to \infty $当$ n\to\infty $时, 这里限制性条件$ \max(0, 2(1-\alpha_0))<\kappa <\frac{3}{2}-\alpha_0 $主要是由于要在$ d_n $的发散性和无穷级数的截断误差之间寻求平衡. 在特殊情况$ \alpha_0=1 $单位根过程时, 我们有$ 0<\kappa<1/2 $和$ d_n\sim \sqrt{n} $.

条件(b)对收敛$ \widehat{\theta}\to_P \theta_0 $有速度的要求, 即$ \zeta_n\to 0 $与$ O(\sqrt{kd_n/n}) $同速. 注意, 关于$ \widehat{\theta}-\theta_0 $的极限理论在一般设定下还没有建立; 在特殊情况下$ \widehat{\theta}-\theta_0 $的收敛速度可以达到$ O_P(\sqrt{d_n/n}) $, 这包括: (i) $ e_t $与$ u_t $独立; (ii) $ (e_t, \mathcal{F}_t) $是鞅差过程, 而$ x_t $对$ \mathcal{F}_{t-1} $适应, 见Park and Phillips(1999, 2001); (iii) 在Dong and Gao (2018)附录C里, 作者提供了一个例子, 在具有内生性的情况下$ \widehat{\theta}-\theta_0 $的收敛速度可以达到$ O_P(\sqrt{d_n/n}) $. 另外, Wang and Phillips (2016)在非平稳过程$ x_t $或者具有短记忆或者具有长记忆的情况下给出了$ \widehat{\theta}-\theta_0 $收敛速率(Theorem 4.2, p14); 在此基础上他们在核估计方法的检验问题中要求$ \widehat{\theta}- \theta_0= O_P(\sqrt{d_n/nh}) $, 这里$ h $是窗宽. 这和我们的要求类似. 鉴于以上讨论, 条件(b)要求在原假设下$ \widehat{\theta}-\theta_0 $的速率是合理的.

注意到Chen, Gao and Li (2011)研究了在对立假设$ H_1: y_t=g(V_t; \theta_1)+\Delta_n(V_t)+e_t $下, $ \theta_1 $的估计, 其中$ V_t=H(t/n)+u_t $, $ \{u_t\} $是i.i.d.序列. 他们提议的$ \theta_1 $的估计量是$ \sum_{t=1}^n (y_t-g(V_t; \theta))^2 $的最小值点, 且证明了估计量的渐近无偏和$ \sqrt{n} $收敛速率, 与模型里没有$ \Delta_n(V_t) $的情形速度相同. 见Chen, Gao and Li (2011)中推论2.4. 另外, Wang and Phillips (2016)假定$ \theta_1=\theta_0 $, 因此在原假设和对立假设下参数的收敛速度相同. 很明显, 我们的对立假设涵盖的范围比Wang and Phillips (2016)更广.

条件(c)是一组对原假设下回归函数的要求, 这在类似情形下的文献里经常遇到, 见Gao, Wang and Yin (2011)假设2.4和Wang and Phillips (2012)假设4. 容易看到下列函数类满足要求: 1) $ g(x;\theta)=\theta g_1(x) $, 这里$ g_1(x) $可积, $ \theta\in \mathbb{R} $ (所谓的参数线性(linear-in-parameter)回归函数, 见Park and Phillips (2001); 2) $ g(x;\theta)= \frac{1}{1+\theta x^2} $, 其中$ \theta>c>0 $; 3) $ g(x;\alpha, \beta) =\alpha\exp (-\beta x^2) $, 其中$ \theta=(\alpha, \beta) \in \Theta\subset \mathbb{R}\times \mathbb{R}^+ $, $ \Theta $是紧集.

假设C.2  令$ \Delta_{n}(x)=\delta_n \Delta(x) $, 且满足

(a) $ \Delta(x) $是非零函数且$ \int \Delta^2(x){\rm d}x<\infty $.

(b) 当$ n\to \infty $, $ \delta_n\to 0 $且$ \delta_n^2 n/(d_nk)\to \infty $, 其中$ k $满足假设B.2(a).

注  条件(a)排除掉零函数$ \Delta(x) $的原因是显然的, 这也意味着$ \int\Delta^2(x) {\rm d}x\ne 0 $. 因此, 我们的检验统计量是一致的, 并且把偏离原假设的程度压缩到尽可能的小. 确实, 零极限$ \delta_n\to 0 $和$ \Delta^2(x) $的可积性蕴含着偏离函数$ \Delta_{n}(x) $随着样本容量增大而越来越小, 而$ \delta_n^2 n/(d_nk) \to \infty $保证了检验统计量具有非凡功效. 为了验证这一点我们在下面的模拟实验里取$ \delta_n $趋于零足够快, 满足$ \delta_n^2 n/(d_nk)= \frac{1}{4}\ln(n) $, 发散的很慢; 在这样的设定下我们的统计量仍然具有识别能力.

识别性检验: 可积情况  回忆第二节内容, 若$ m(\cdot)\in L^2(\mathbb{R}) $, 那么$ m(x)= \sum_{i=0}^\infty \beta_{i}\mathscr{H}_i(x) $. 令$ k $为正整数, 定义$ m_{k}(x)=\sum_{i=0}^{k-1} \beta_{i} \mathscr{H}_i (x) $和$ \gamma_k(x)= \sum_{i=k}^\infty \beta_{i} \mathscr{H}_i (x) $, $ x\in \mathbb{R} $. 记$ Z(x)= (\mathscr{H}_0(x), \cdots, \mathscr{H}_{k-1}(x))^\top $, $ \beta= (\beta_{0}, \cdots, \beta_{k-1})^\top $, 从而$ m_{k}(x)=Z(x)^\top\beta $.

模型(30)在原假设$ H_0 $下写为$ y_t=Z(x_t)^\top\beta+\gamma_k(x_t)+e_t $, $ t=1, \cdots, n $. 记$ Y=(y_1, \cdots, y_n)^\top $, $ Z=(Z(x_1), \cdots, Z(x_n))^\top $为一个$ n\times k $矩阵, 向量$ e=(e_1, \cdots, e_n)^\top $, $ \gamma=(\gamma_k(x_1), \cdots, \gamma_k(x_n))^\top $. 那么模型的矩阵形式为:

(33) $ \begin{equation} Y=Z\beta+\gamma+e. \end{equation} $

因此, $ \beta $的最小二乘法估计量为$ \widehat{\beta} = (Z^\top Z)^{-1}Z^\top Y $. 从而定义$ \widehat{m}(x)=Z(x)^\top\widehat{\beta} $为$ m(x) $的估计量, $ \forall \, x\in \mathbb{R} $.

因为矩阵$ Z'Z $的维数发散, 且包含非线性非平稳时间序列, 这在理论分析和计算上都会带来困难. 为了避免$ \widehat{\beta} $中的这个逆矩阵, 我们取$ \widetilde{\beta}= Z^\top Z \widehat{\beta} $和相应的函数$ \widetilde{m}(x)= Z(x)^\top \widetilde{\beta} $构造检验统计量. 从$ \widehat{\beta} $的表达式可得,

(34) $ \begin{align} \widetilde{m}(x)=\sum\limits_{t=1}^n [Z(x_t)^\top Z(x)] y_t. \end{align} $

如下面式(40)所讨论, 这种剔除$ (Z^\top Z)^{-1} $处理方式首先由Dong et al. (2017)的工作论文在核估计构造统计量所采用, 然后被Wang and Phillips (2016)延用. 我们的经验显示, 在级数估计里去除$ Z^\top Z $的逆和在核估计里去除随机的分母项不仅会简化理论分析, 而且会提高有限样本下统计量的表现.

类似地, 我们构造$ g(x;\theta) $的相应表达式$ \widetilde{g}(x; \theta) $,

(35) $ \begin{equation} \widetilde{g}(x;\theta)=\sum\limits_{t=1}^n [Z(x_t)^\top Z(x)] g(x_t;\theta). \end{equation} $

注意到$ \widehat{\theta} $是原假设$ H_0: \ y_t = g(x_t; \theta_0) + e_t $下$ \theta_0 $的相合估计, 我们度量$ \widetilde{m}(x) $和$ \widetilde{g}(x; \widehat{\theta}) $之间的距离并提出检验统计量:

(36) $ \begin{equation} L_n=\int_{-\infty}^\infty \left(\widetilde{m}(x) -\widetilde{g}(x; \widehat{\theta}) \right)^2{\rm d}x =\int_{-\infty}^\infty \left(\sum\limits_{t=1}^n [Z(x_t)^\top Z(x)](y_t- g(x_t; \widehat{\theta})) \right)^2{\rm d}x, \end{equation} $

进一步由基函数的正交性可简化为:

(37) $ \begin{equation} L_n = \sum\limits_{t=1}^n \sum\limits_{s=1}^n Z(x_t)^\top Z(x_s) \widehat{e}_t \widehat{e}_s, \end{equation} $

这里$ \widehat{e}_t:=y_t-g(x_t; \widehat{\theta}) $.

显然, $ L_n $可解释为在空间$ L^2(\mathbb{R}) $里基于观测值$ (y_t, x_t) $, $ m(x) $和$ g(x, \widehat{\theta}) $各自的代表性函数之间的距离. 另外, 在原假设下$ \widehat{e}_t =e_t+[g(x_t;\theta_0)- g(x_t;\widehat{\theta})] $由两个误差项构成; 像下面定理3.7和3.8所证明, $ L_n $经过适当的标准化收敛于布朗运动局部时过程, 而在对立假设下则发散于无穷.

将$ L_n $分解:

(38) $ \begin{equation} L_n = \sum\limits_{t=1}^n \|Z(x_t)\|^2\widehat{e}_t^2 + 2 \sum\limits_{t=2}^n \sum\limits_{s=1}^{t-1} Z(x_t)^\top Z(x_s) \widehat{e}_t\widehat{e}_s \equiv L_{an} + L_{bn}. \end{equation} $

如果$ x_t $是平稳变量, Gao, Tong and Wolff (2002)证明, $ L_{an} $适当的标准化将依概率收敛于一个非随机的量. 于是, 人们不得不构造

(39) $ \begin{equation} \widehat{L}_{bn} = \frac{\sum\nolimits_{t=2}^n \sum\nolimits_{s=1}^{t-1} \widehat{e}_s Z(x_t)^\top Z(x_s) \widehat{e}_t}{ \sqrt{ \sum\nolimits_{t=2}^n \sum\nolimits_{s=1}^{t-1} \widehat{e}_s^2 \left(Z(x_t)^\top Z(x_s)\right)^2 \widehat{e}_t^2}} \end{equation} $

得到相合检验统计量. 在非平稳情形下, 我们将证明$ L_{an} $是主项, 它收敛于局部时变量, 而相比较$ L_{an} $而言, $ L_{bn} $可渐近忽略. 我们提到的另一个检验, 首先由Dong et al. (2017)工作论文提出, 再由Wang and Phillips (2016)延续使用的核估计检验:

(40) $ \begin{equation} \widetilde{L}_{n} = \int_{-\infty}^{\infty} \left(\widehat{q}(x) - \widetilde{q}\left(x; \widehat{\theta}\right)\right)^2 \pi(x){\rm d}x, \end{equation} $

其中$ \widehat{q}(x) = \frac{1}{\sqrt{n} h} \sum_{t=1}^n K\left(\frac{x_t - x}{h}\right) y_t $, $ \widetilde{q}(x; \theta) = \frac{1}{\sqrt{n} h} \sum_{t=1}^n K_1\left(\frac{x_t - x}{h}\right) g(x_t; \theta) $, $ \pi(\cdot) $是概率密度. 统计量$ \widetilde{L}_n $的一个缺点是它包含了任意选取的权函数$ \pi(\cdot) $. 相反, $ L_n $标准化$ \frac{\widehat{d}_n}{nk \ \widehat{\sigma}^2_e}L_n $ (见定理3.7) 既不包含权函数又不包含随机性分母. 因此, 式(36)中$ L_n $才使得下面的定理在两种内生性存在情况下成为可能.

定理3.7  假设A.2和B.2成立. 在原假设$ H_0 $下, 当$ n\to \infty $我们有:

(41) $ \begin{equation} \frac{d_n}{nk \, \sigma_e^2}L_{n}\rightarrow_D L_W(1, 0), \end{equation} $

其中$ \sigma_e^2=E[e_1^2] $, $ d_n=\sqrt{E(x_n^2)} $, $ L_W(1, 0) $是$ W(r; \alpha_0) $的局部时随机变量.

定理3.8  假设A.2$ \sim $C.2成立. 在对立假设$ H_1 $下, 当$ n\to \infty $时,

(42) $ \begin{equation} \frac{d_n}{nk \, \sigma_e^2}L_{n}\to_P \infty. \end{equation} $

本节的所有证明请参考Dong and Gao (2018). 定理3.7给出了检验统计量的极限分布. 定理3.8表明检验统计量针对局部对立假设序列具有非凡功效, 因为在$ H_1 $下, $ \widehat{e}_t= e_t+ [g(x_t;\theta_1)- g(x_t;\widehat{\theta})] +\Delta_{n}(x_t) $, 其中$ \widehat{\theta} $是$ \theta_1 $的相合估计量. 即使对立假设偏离原假设的偏离函数$ \Delta_{n}(x_t) $趋于零, 但是速度不快于$ (kd_n/n)^{1/2} $, 保证了检验功效. 这种情形类似于Gao (2017)第三章在平稳情形下的讨论. 可以从定理的证明里看到, 在对立假设下$ \frac{d_n}{nk \, \sigma_e^2}L_n $以$ O_P(\delta_n^2n/d_nk) $发散于无穷. 有了定理3.7和3.8, 我们可以辨别在模型里到底是假设$ H_0 $还是$ H_1 $成立; 如果$ \frac{d_n}{nk \, \sigma_e^2}L_n $足够大, 我们拒绝$ H_0 $而倾向于$ H_1 $成立.

假设A.2可以用来估计线性过程$ u_t $中的未知参数. 见Hualde and Robinson $ (2011, {\rm p}3155) $. 更为重要的是, 由A.2(b), $ \Psi({\rm e}^{i\nu}; \rho) $的导数的傅里叶系数满足$ j\psi_j(\rho)= O(j^{-\varsigma}) $当$ j\to \infty $时, $ \forall\, \rho $, 那么, 由$ \Xi $的紧性和$ \psi_j(\rho) $的连续性,

(43) $ \begin{equation} \sup\limits_{\rho\in \Xi}|\psi_j(\rho)|=O(j^{-(1+\varsigma)}), \qquad j\to \infty. \end{equation} $

注意, $ w_t=\Psi^{-1}(L;\rho_0)u_t=\Psi^{-1}(L;\rho_0) \Delta^{\alpha_0} x_t $, $ t\ge 1 $. 对于$ \tau=(\rho^\top, \alpha)^\top $, 定义,

(44) $ \begin{equation} w_t(\tau)=\Psi^{-1}(L;\rho)\Delta^{\alpha} x_t, \end{equation} $

和

(45) $ \begin{equation} \widehat{\tau}=\underset{ \tau\in \Xi} {\text{argmin}}\frac{1}{n}\sum\limits_{t=1}^n w_t^2(\tau) \end{equation} $

作为$ \tau_0=(\rho^\top_0, \alpha_0)^\top $的估计量.

引理3.1  定义$ \widehat{\psi}=\psi(\widehat{\rho})= \sum_{j=0}^\infty \psi_j(\widehat{\rho}) $, $ \widehat{d}_n= |\widehat{\psi}| \Gamma^{-1}(\widehat{\alpha}) n^{\widehat{\alpha}-1/2} $, $ \widehat{\sigma}_e^2= \frac{1}{n} \sum_{t=1}^n \widehat{e}_t^2 $, $ \widehat{e}_t=y_t-g(x_t, \widehat{\theta}) $, $ \widehat{L}_W(1, 0)= \frac{\widehat{d}_n}{n} \sum_{t=1}^n\mathscr{H}_0^2(x_t) $. 那么, 在假设A.2和$ H_0 $下, 当$ n\to \infty $,

(46) $ \begin{equation} \widehat{\psi}\to_P \psi, \quad \frac{\widehat{d}_n}{d_n}\to_P 1, \quad \widehat{\sigma}_e^2\to_P\sigma_e^2, \quad \text{和}\quad \widehat{L}_W(1, 0)-L_W(1, 0)\to_P 0. \end{equation} $

定理3.9  当$ \psi $和$ \sigma_e^2 $均未知, 在原假设$ H_0 $和A.2$ \sim $B.2下, 我们有:

(47) $ \begin{equation} \frac{\widehat{d}_n}{nk \, \widehat{\sigma}^2_e}L_n\to_D L_W(1, 0), \end{equation} $

这里$ \widehat{d}_n $, $ \widehat{\sigma}^2_e $在引理3.1中定义. 在对立假设$ H_1 $和A.2$ \sim $C.2下, 当$ n\to \infty $,

(48) $ \begin{equation} \frac{\widehat{d}_n}{nk \, \widehat{\sigma}^2_e}L_n\to_P \infty. \end{equation} $

统计量$ \widehat{M}_n \equiv \frac{\widehat{d}_n}{nk\, \widehat{\sigma}^2_e} L_n $不仅具有大样本性质而且它现在完全可以由观测值计算. 由此定理, 给定显著性水平$ \nu $, 定义$ l_{1-\nu} $满足$ P(L_W(1, 0)>l_{1-\nu})=\nu $; 如果$ \widehat{M}_n> l_{1-\nu} $, 我们可以拒绝$ H_0 $.

识别性检验: 不可积情况  我们把限制条件$ m(x) $属于$ L^2(\mathbb{R}) $放宽到$ m(x) $属于$ L^2(\mathbb{R}, \exp(-x^2)) $. 我们的动机是, 如果$ m(x) $满足$ \int m^2(x){\rm e}^{-x^2}{\rm d}x<\infty $, 那么$ m(x)\exp(-x^2/2)\in L^2 (\mathbb{R}) $. 因此, 经过简单变换我们可以借用$ L_n $来识别不可积回归函数模型.

给定观测值$ \{(x_t, y_t), t=1, 2, \cdots, n\} $满足模型(30), 我们要检验,

(49) $ \begin{equation} H_{10}: \ \ m(x)=g(x;\theta_0) \ \ \ \mbox{v.s.}\ \ \ H_{11}: \ \ m(x)=g(x;\theta_1) +\Delta_{n}(x), \end{equation} $

其中, 对于任意$ \theta\in \Theta\subset \mathbb{R}^d $, $ g(x; \theta)\in L^2 (\mathbb{R}, \exp(-x^2)) $是已知函数, 而$ \Delta_{n}(x) $与假设C.2同.

为了利用统计量$ L_n $, 模型两边同乘$ \varphi(x_t):= \exp(-\frac{1}{2}x^2_t) $得到可积模型. 具体而言, 记$ Y_t=y_t \varphi(x_t) $, $ M(x_t)=\varphi(x_t)m(x_t) $, $ \varepsilon_t= \varphi(x_t) e_t $, 我们有:

(50) $ \begin{equation} Y_t=M(x_t)+\varepsilon_t, \qquad t=1, \cdots, n. \end{equation} $

注意, $ H_{10} $完全等价于$ H_{10}':\ M(x)= G(x;\theta_0) $, 其中$ G(x; \theta) = g(x;\theta)\varphi(x) $, 而$ H_{11} $则完全等价于$ H_{11}': \ M(x)=G(x;\theta_1)+ \Delta_{n}(x) \varphi(x) $. 这其中的$ M(x) $是未知可积函数, $ G(x;\theta) $是已知可积函数. 粗略地说, 我们把"不可积"数据$ (y_t, x_t) $转换成"可积"数据$ (Y_t, x_t) $. 注意, $ H_{11}' $中偏离函数$ \Delta_{n}(x) \varphi(x) $与$ H_{11} $中$ \Delta_{n}(x) $具有相同性质, 非零且可积. 所以, 经过转换我们面临以前的老问题了. 我们因此为假设(49)提出下述检验统计量:

(51) $ \begin{align} \Pi_n=\sum\limits_{t=1}^n \sum\limits_{s=1}^n Z(x_t)^\top Z(x_s)\widehat{\varepsilon}_t \widehat{\varepsilon}_s, \end{align} $

这里$ \widehat{\varepsilon}_t:=\widehat{e}_t\varphi(x_t)=(y_t- g(x_t; \widehat{\theta})) \varphi(x_t)=Y_t-G(x_t; \widehat{\theta}) $, $ \widehat{\theta} $是$ \theta_0 $的相合估计量.

虽然$ \Pi_n=\sum_{t=1}^n \sum_{s=1}^n Z(x_t)^\top Z(x_s)\varphi(x_t) \varphi(x_s) \widehat{e}_t \widehat{e}_s $, 但是在$ H_{10} $下, $ \widehat{e}_t=y_t- g(x_t;\widehat{\theta})=e_t+g(x_t;\theta_0) -g(x_t;\widehat{\theta}) $, 而在$ H_{11} $下, $ \widehat{e}_t=y_t- g(x_t;\widehat{\theta})=e_t+g(x_t;\theta_0) -g(x_t;\widehat{\theta}) +\Delta_{n}(x_t) $. 与$ L_n $相比, $ \Pi_n $的每一项多了因子$ \varphi(x_t)\varphi(x_s) $, 这正是由$ m(x_t) $到$ M(x_t) $的变换带来的后果.

在陈述$ \Pi_n $的极限理论之前, 我们先给出下列假设, 它和假设B.2类似, 只不过是针对$ m $属于$ L^2(\mathbb{R}, \exp(-x^2)) $的情形.

假设B*.2

(a) 设$ k $满足假设B.2(a).

(b) 在原假设(49)下, 存在$ \theta_0 $相合估计量, $ \widehat{\theta} $, 使得对于任何$ \varepsilon_0>0 $和某个$ 0<M=M(\varepsilon_0)<\infty $, 有$ P(\|\widehat {\theta} -\theta_0\| > M \, \zeta_n) < \varepsilon_0 $, 这里$ \zeta_n \sqrt{\frac{n}{kd_n}}=O(1) $. 当把$ \theta_0 $替换成$ \theta_1 $, 这个假设在$ H_{11} $下也成立.

(c) 假定$ g(x;\theta) $关于$ \theta $二次可微. 令$ l_1(x, \theta):= \frac{\partial}{\partial \theta} g(x;\theta) $, $ l_2(x, \theta):= \frac{\partial^2}{\partial\theta \partial \theta^\top} g(x;\theta) $. 进一步假设$ \|l_1(x, \cdot)\|, \|l_2(x, \cdot)\|\in L^2(\mathbb{R}, {\rm e}^{-x^2}) $, 且存在正函数$ l(x)\in L^2(\mathbb{R}, {\rm e}^{-x^2}) $使得$ \|l_2(x, \theta)\|\le l(x) $对$ \theta $一致成立.

假设B*.2和B.2存在两点区别. 首先, $ \theta_0 $的估计是在$ H_{10} $下得到, 而我们并没有在B*.2(b)里对估计量提出更快的收敛速度要求, 虽然在文献里不可积的回归函数的估计量的收敛远远快于$ \sqrt{d_n/n} $. 这是我们估计量的优点, 因为不可积的函数$ m(x) $被转换为可积函数$ M(x) $, 所以$ \Pi_n $的工作环境与$ L_n $相同. 因此, 文献里研究的所有回归函数都满足这里的条件. 比如, 多项式, 幂函数, $ \theta \log |x| $, $ \theta {\rm e}^x/(1+{\rm e}^x) $和$ x(1+\theta x)^{-1}1 (x\ge 0) $, 其收敛速率都快于可积类函数. 详细的讨论可见Park and Phillips (2001)中定理5.2和5.3.

另一点区别是函数空间. 现在$ m(x) $属于$ L^2(\mathbb{R}, {\rm e}^{-x^2}) $, 所以我们要求其对参数的偏导数的模属于$ L^2(\mathbb{R}, {\rm e}^{-x^2}) $. 显然, 上面的例子都满足这些条件.

定理3.10  设A.2和B*.2成立. 在$ H_{10} $下, 当$ n\to \infty $我们有:

(52) $ \begin{equation} \frac{d_n}{nk \, \sigma_e^2}\Pi_{n}\to_D \int \mathscr{T}(x)\varphi^2(x){\rm d}x \cdot L_W(1, 0), \end{equation} $

这里$ \sigma_e^2=E[e_1^2] $, 当$ x\in [-2, 2] $, $ \mathscr{T}(x)=\frac{1}{2 \pi}\sqrt{4-x^2} $, 否则$ \mathscr{T}(x)=0 $, $ \varphi(x)= \exp(-\frac{1}{2}x^2) $, 而$ d_n $和$ L_W(1, 0) $与前面定理同义. 如果用引理3.1所定义的$ \widehat{d}_n $和$ \widehat{\sigma}_e^2 $分别替换$ d_n $和$ \sigma_e^2 $, 我们得到可行的检验统计量.

设A.2, B*.2和C.2成立. 在$ H_{11} $下, 当$ n\to \infty $我们有:

(53) $ \begin{equation} \frac{d_n}{nk \, \sigma_e^2}\Pi_{n}\to_P \infty. \end{equation} $

同样的, 如果用引理3.1所定义的$ \widehat{d}_n $和$ \widehat{\sigma}_e^2 $分别替换$ d_n $和$ \sigma_e^2 $, 我们得到可行的检验统计量.

注  式(52)结果与式(41)的结果相类似, 只是要注意$ \int \mathscr{T}(x){\rm d}x=1 $. 由于$ \Pi_{n} $包含函数$ \varphi(\cdot) $, 定理3.10的证明非常类似于定理3.7和3.8. 假设C.2在可积与不可积的情形都用到了, 因为可积函数通常小于不可积函数, 尤其是在远离原点的区域, 因此如果我们的统计量对于可积的偏离函数适用, 那它也适用于不可积的偏离函数. 其实非常清楚, 只要$ \Delta^2(x){\rm e}^{-x^2} $可积, 统计量$ \Pi_n $就是一致的, 意味着$ \Delta(x) $可以取多项式, 幂函数和有界函数, 更不用说可积函数了. 所以我们在两种情形下都使用了假设C.2. 因为在对立假设下$ \frac{d_n}{nk \, \sigma_e^2} \Pi_n =O_P(\delta_n^2n/d_nk) $仍然成立, 这一点也不影响$ \Pi_n $的检验功效.

蒙特卡罗实验  我们将通过蒙特卡罗模拟实验考察检验统计量$ L_n $和$ \Pi_n $在有限样本情形下的表现. 为了与假设A.2相一致, 考虑两种数据生成机制:

(Ⅰ) 假定$ \{\epsilon_j, j\in \mathbb{Z}\} $是i.i.d. $ N(0, \sigma^2) $序列. 令$ e_t=\beta_0e_{t-1}+ \epsilon_t $, $ |\beta_0|<1 $, $ u_t=\alpha_0 u_{t-1}+ \epsilon_t $, $ |\alpha_0|<1 $, $ x_t=x_{t-1}+u_t $, $ x_0=O_P(1) $.

(Ⅱ) 假定$ \{(\epsilon_j, \eta_j), j\in \mathbb{Z}\} $是i.i.d. $ N(0, \sigma^2I_2) $序列. 令$ e_t=a \epsilon_{t}+ b\eta_t $, $ u_t=\alpha_0 u_{t-1}+ \epsilon_t $, $ |\alpha_0|<1 $, $ x_t=x_{t-1}+u_t $, $ x_0=O_P(1) $.

假设里所有的常数随后将会给出. 在第一种生成机制里, 如果$ \alpha_0=\beta_0 $, 则$ e_t=u_t $, 反映了最高的相依性; 在第二种生成机制里, 如果$ a=0 $, $ e_t=b\eta_t $与所有$ \epsilon_{j} $独立, 从而与$ u_t $独立, 所以$ e_t $和$ x_t $独立, 意味着外生性.

Bootstrap模拟程序: 我们采用bootstrap程序来生成临界值$ l_\alpha^* $, 其中$ \alpha =1\% $和10%. 蒙特卡罗模拟重复次数$ M=5000 $, bootstrap重复次数$ M_b=250 $. 因机制(I)包括一个AR(1)模型, 我们使用块bootstrap方法(block bootstrap), 而回归bootstrap方法在机制(II)情形使用.

Step 1  令$ \widehat{e}_t = y_t - g(x_t, \widehat{\theta}) $, 这里$ \widehat{\theta} $是在原假设下基于观测值$ (x_t, y_t) $的$ \theta_0 $的相合估计. 生成$ e_t^{\ast} $如下.

(a) 对于机制(I), 采用通常的块bootstrap方法生成$ e_t^{\ast} $ (参见Hall, Horowitz and Jing (1995)): 用模型$ \widehat{e}_t = \beta_0 \widehat{e}_{t-1} + \epsilon_t $估计$ \beta_0 $得$ \widehat{\beta}_0 $, 然后由$ \widehat{\sigma}^2 = \frac{1}{n} \sum_{t=1}^n (\widehat{e}_t - \widehat{\beta}_0 \widehat{e}_{t-1})^2 $估计$ \sigma^2 $.

令$ l=[n^{\frac{1}{3}}] $, 取整数$ \lambda $满足$ \lambda l=n $. 在第$ j $步生成$ e_{1, l}^{\ast }(j)= \left[ \widehat{e}_{1}(j), \cdots, \widehat{e}_{l}(j)\right] $, $ \cdots $, $ e_{\lambda, l}^{\ast } (j)=\left[ \widehat{e}_{(\lambda-1)l+1}(j), \cdots, \widehat{e}_{\lambda l}(j)\right] $. 经过重复抽样$ J=250 $次, 得到$ J $个bootstrap样本$ \{e_{sl}^{\ast }(j):1\leq s\leq \lambda;1\leq j\leq J\} $, 取平均$ e_{sl}^{\ast }=\frac{1}{J}\sum_{j=1}^{J} e_{sl}^{\ast }(j) $得到块bootstrap $ e_{t} $: $ \left(e_{1}^{\ast}, \cdots, e_{n}^{\ast }\right) =\left(e_{1l}^{\ast }, \cdots, e_{\lambda l}^{\ast}\right) $.

(b) 对于机制(II), 用回归bootstrap方法生成$ e_t^{\ast} $ (参见Li and Wang (1998)) $ e_t^{\ast}=\widehat{e}_t\tau_t $, 这里$ \tau_t $是i.i.d. 序列, 服从两点分布$ P(\tau_1=\mp (\sqrt{5}\mp 1)/2)=(\sqrt{5}\pm 1)/2\sqrt{5} $.

Step 2  用$ y_t^{\ast} = g(x_t, \widehat{\theta}) + e_t^{\ast} $生成$ y_t^{\ast} $. 由$ (x_t, y_t^{\ast}) $重新估计$ \theta_0 $, 得$ \widehat{\theta}^* $. 利用$ L_n $的表达式, 但是把$ \widehat{\theta} $和$ \{(x_t, y_t), 1\le t\le n\} $分别用$ \widehat{\theta}^* $和$ \{(x_t, y_t^*), 1\le t\le n\} $替换, 来计算得到$ L_n^* $.

Step 3  重复以上步骤$ M_b $次, 得到$ M_b $个$ L_n^* $, 记为$ L^*_{n\ell} $, $ \ell=1, \cdots, M_b $. 利用这$ M_b $个$ L^*_{n\ell} $值构造经验bootstrap分布函数. 给定$ \mathcal{W}_n =\{(x_t, y_t), 1\le t\le n\} $, $ \frac{d_n}{nk}L^*_{n} $的bootstrap分布定义为$ P^*(\frac{d_n}{nk} L^*_{n}<x) =P (\frac{d_n}{nk}L^*_{n}<x |\mathcal{W}_n) $. 令$ l_\alpha^* $为分位数, 使得$ P^*(\frac{d_n}{nk} L^*_{n}\ge l_\alpha^*)=\alpha $, 那么$ l_\alpha^* $就是$ l_\alpha $的近似.

Step 4  定义检验水平和功效函数(the size and power functions) 为:

$ \begin{equation*} \alpha=P\left(\frac{d_n}{nk}L_n\ge l_\alpha^*|H_0\right)\ \ \text{和}\ \ \beta=P\left(\frac{d_n}{nk}L_n\ge l_\alpha^*|H_1 \right). \end{equation*} $

在实验中样本容量分别取$ n=200, 500 $和$ 1200 $, 截断参数$ k=[c\cdot n^{\kappa}] $, $ \kappa=1/5, 1/4.5, 1/4 $, 并且$ c=2.2 $. 令$ \Delta_n(x)=\delta_n \frac{1}{1+x^2} $, 其中$ \delta_n= \frac{1}{2} \sqrt{k\log(n) /\sqrt{n}} $. 很清楚, 我们取的$ \delta_n $和$ \Delta(x) $都"很小", 因为$ \Delta(x)=\frac{1}{1+x^2} $可积而$ \delta_n $趋于零很快, 使得$ \delta_n^2\sqrt{n}/k = \frac{1}{4} \log(n) $. 虽然$ \delta_n^2\sqrt{n}/k $的发散性是检验统计量一致性的必要条件, 但是我们让它发散的很慢. 我们在$ \psi $和$ \sigma_e^2 $未知的情况下考察$ L_n $和$ \Pi_n $, 所以我们用估计量$ \widehat{\sigma}_e^2 $替代$ \sigma_e^2 $, 但是因为$ \psi $包含在$ x_t $里, 而我们用bootstrap方法生成临界值, 实验里并没有使用$ \widehat{\psi} $.

例3.3  本例考察统计量$ L_n $, 为此考虑模型$ y_t=m(x_t)+e_t $.

在机制(I)下, 原假设$ H_0 $: $ P(m(x_t)=10 \exp (-\theta_0 x^2_t))=1 $, $ \theta_0=1 $; 对立假设$ H_1 $: $ P(m(x_t)=10 \exp (-\theta_1 x^2_t) +\Delta_n(x_t))=1 $, $ \theta_1=1 $.

在机制(II)下, 原假设$ H_0 $: $ P(m(x_t)=(1+x^2_t)\exp (-\theta_0 x^2_t))=1 $, $ \theta_0=1 $; 对立假设$ H_1 $: $ P(m(x_t)=(1+x^2_t)\exp (-\theta_1 x^2_t)+\Delta_n(x_t))=1 $, $ \theta_1 =1 $.

在表 4~7我们报告检验水平和功效. 表 4和6是所有的检验水平的实验结果, 可以看到几乎所有的检验水平都围绕着给定的显著性水平波动. 在表 6中, 略低于一半的实验结果低于给定的显著水平, 而在表 4里绝大多数的结果都超过这个显著水平. 另外, 在表 6里, 尽管由于$ a=0 $, $ e_t $和$ x_t $相互独立, 检验水平的表现与$ a=0.2 $的情形类似. 总的来说, 当样本容量增大时检验水平表现稳定.

表 5和7涵盖了一些重要情形. 虽然局部偏离函数$ \Delta_n(x)= \delta_n \Delta(x) $随着$ \delta_n $趋于零而可渐近忽略, 检验功效还是很强. 容易看到, 或者样本容量增加或者截断参数$ \kappa $增加在大多数实验中都能导致检验功效增加. 这是因为二者的增加都会使得$ L_n $包含更多的基函数, 从而由定理3.8的证明看到, 每增加一个基函数都会提高检验功效. 同时, 比较表 7里内生性和外生性的结果看到, 内生性并不会降低检验功效, 相反功效在所有的实验里都表现的很强很稳健.

例3.4  为了考察统计量$ \Pi_n $, 考虑模型$ y_t=m(x_t)+e_t $.

在机制(I)下, 原假设$ H_{10} $: $ P(m(x_t)=\theta_0 x^2_t(x_t+ \sin(x_t)))=1 $, $ \theta_0=1 $; 独立假设$ H_{11} $: $ P(m(x_t)=\theta_1 x^2_t(x_t+\sin(x_t))+ \Delta_n(x_t))=1 $, $ \theta_1=1 $.

在机制(II)下, 原假设$ H_{10} $: $ P(m(x_t)=\theta_0 x^2_t(2+x_t +\sin(x_t)))=1 $, $ \theta_0=1 $; 对立假设$ H_{11} $: $ P(m(x_t)=\theta_1 x^2_t(2+x_t+\sin(x_t))+ \Delta_n(x_t))=1 $, $ \theta_1=1 $.

表 8和10报告了两种数据生成机制下的检验水平的实验结果. 可以看到, 低于显著水平的实验结果占了较大比例, 尤其是表 10. 另外表 10里, 在1% 水平上, 当$ \kappa=1/4.5 $时检验水平即使在$ n=1200 $也与显著水平有一定距离. 然而, 几乎所有的检验水平都会随着样本容量的增加而趋于显著水平, 大体上表现满意.

表 9和11给出了所有检验功效的实验结果. 检验功效随着样本容量的增加或者$ \kappa $的增加而增加, 表现很强很稳健. 这和例3.3的原因是一样的. 值得注意的是, 表 11中两个实验的功效有明显区别, 这可能是由于参数$ \alpha_0, \ a $和$ b $的选择或者一些不明原因所导致的.

就时间序列而言, 有三种变量在经济、金融和相关领域随处可见, 它们是非随机时间趋势、平稳变量和非平稳变量. 比如, 总消费、可支配性收入和股票价格均为非平稳变量, 而利率和股票交易量常常认为是平稳变量或者具有微弱趋势的局部平稳变量. 因此, 从实用的角度来看, 我们有必要研究这种回归模型, 它们的回归变量涵盖这三种类型的变量.

Grenander and Rosenblatt (1957)是经典的时间趋势参数模型, 而Phillips(2007, 2010)进行了后续研究. 文献里有相当多的文章研究非平稳非参数回归模型. Karlsen, Mykelbust and Tjøstheim (2007)研究非参数回归, 其标量协变量是一个马尔可夫链. Schienle (2008)研究非参数可加模型, 其协变量为哈里斯常返(Harris recurrent) 时间序列并得到核光滑回溯估计量(kernel smooth backfitting estimators)的极限理论. Wang and Phillips (2009a)考虑了非参数单位根回归的核估计. Phillips, Li and Gao (2017)考虑了函数型系数模型, 其协变量为单位根过程而函数型系数则以时间趋势为变量. Wang (2015)是一部优秀的著作, 回顾了关于非平稳时间序列的极限理论.

就我们所知, 很少有文章研究涵盖三种变量的非参数模型. 在Chang, Park and Phillips (2001)中, 虽然三种变量都包含在回归方程里, 但它研究的是非线性参数模型, 即所有的函数都是已知的. 除此之外, 有些文章研究的模型包含了以上提到的三种变量里的两种, 比如Park and Hahn (1999), Xiao (2009), Cai, Li and Park (2009), Li, Phillips and Gao (2016).

我们在这里考虑模型:

(54) $ \begin{equation} y_{t}=\beta(t/n)+g(z_{t})+m(x_{t})+e_{t}, \text{ }t=1, \cdots, n, \end{equation} $

其中$ \beta, g $和$ m $是未知光滑函数, $ z_{t} $和$ x_{t} $分别是平稳和单整过程, 二者有可能相关, $ e_{t} $是误差项. 这里, $ \beta(\cdot) $定义于$ [0, 1] $, $ g(\cdot) $定义于$ z_{1} $的支撑集$ V_{z} $, $ m(\cdot) $定义于$ \mathbb{R} $且可积. 注意, $ V_{z} $可能是有限区间$ [a, b] $, 也可能是像$ (-\infty, \infty) $或者$ (0, \infty) $无限区间.

我们将对所有未知函数采用级数估计法估计; 可以说, 相比于核方法所需要的回溯技术("backfitting technique", 见Mammen, Linton and Nielsen (1999)), 级数估计对于可加模型是非常方便的(Andrews and Whang (1990)). 确实, 级数估计方法通过最小二乘估计可以得到显式解, 有利于渐近分析. 相反, 回溯方法则需要两步才能得到估计量. 参见Vogt (2012).

模型(54)最重要的特点是解释变量种类的多样性, 从而其应用范围非常广泛. 但是, 它在极限理论上也带来巨大的挑战. 我们的发现包括: 1) 经过适当的标准化, $ m(x_{t}) $与另外两个可加函数的交互作用最终都会消失; 2) 虽然在估计量里相互纠缠在一起, 每一个未知函数的估计量有各自的收敛速度; 3) 传统的非参数最优收敛速度是可以达到的.

模型假设和估计  我们先给出单整回归变量$ x_{t} $的生成过程.

假设A.3

(a) 设$ \{\epsilon_{j}, -\infty<j<\infty\} $是独立同分布的连续型标量序列, 满足$ E[\epsilon_{1}]=0, E[\epsilon_{1}^{2}] =1, E|\epsilon_{1}|^{q_{1}} <\infty $, $ q_{1}\ge4 $. $ \epsilon_{1} $的特征函数满足条件$ \int|\lambda| |E\exp(i\lambda\epsilon_{1})| {\rm d}\lambda<\infty $.

(b) 令$ w_{t}=\sum_{j=0}^{\infty}\psi_{j} \epsilon_{t-j} $, 其中$ \sum _{j=0}^{\infty}j |\psi_{j}|<\infty $, $ \psi:=\sum_{j=0}^{\infty} \psi_{j}\ne0 $.

(c) 对于$ t\ge1 $, $ x_{t}=x_{t-1}+w_{t} $, $ x_{0}=O_{P}(1) $.

假设A.3里关于单位根序列的假设是文献里常见的条件, 参见Park and Phillips (1999, 2001), Dong, Gao and Tjøstheim (2016). 独立同分布序列$ \{\epsilon_{j}\} $是线性过程$ w_{t} $的基石, 而$ w_{t} $又生成了单整协变量$ x_{t} $, $ x_{t} $所有性质都是由这里的$ I(1) $结构推导而来.

注意, 由$ w_{t} $的BN分解Phillips and Solo $ (1992, {\rm p}972) $可得, $ d_{n}^{2} :=E(x_{n}^{2})=\psi^{2}n(1+o(1)) $. 因此, 对于$ r\in\lbrack0, 1] $, 在空间$ D[0, 1] $里当$ n\rightarrow \infty $时, $ d_{n}^{-1}x_{[nr]}\rightarrow_{D}W(r) $, $ [\cdot] $代表最大整数部分. 这里, $ D[0, 1] $是$ [0, 1] $上的思科罗霍德空间(Skorokhod space), 即所有定义于$ [0, 1] $上每一点都右连续且左极限存在的函数集合; $ W(r) $是标准布朗运动, 我们的理论将涉及到它的局部时过程$ L_{W}(r, a)= \lim\limits_{\epsilon\rightarrow0} \epsilon^{-1}\int_{0}^{r}I(|W(u)-a|<\epsilon){\rm d}u, $其中$ I(\cdot) $是示性函数.

假设B.3

(a) 假定$ z_{t} $或者(i)是严格平稳且$ \alpha $-混合过程($ \alpha $-mixing process), 其混合系数$ \alpha(i) $满足, 对于某个$ \delta>0 $, $ \sum_{i=1}^{\infty}\alpha^{\delta/(2+\delta)} (i)<\infty $, 而且$ z_{t} $独立于$ \{\epsilon_{j}, -\infty<j<\infty\} $ (A.3里定义); 或者(ii) $ z_{t}=\rho(\epsilon_{t}, \cdots, \epsilon_{t-d+1}; \eta_t, \cdots, \eta_{t-d+1}) $, $ d \ge 1 $固定, 函数$ \rho: \mathbb{R}^{2d}\mapsto \mathbb{R} $, 使得$ z_t $具有有限二阶矩, 这里i.i.d.$ (0, 1) $序列$ \{\eta_j\} $独立于序列$ \{\epsilon_j\} $.

(b) 存在定义于支撑集$ V_{z} $上关于$ {\rm d}F(z) $正交的函数序列$ \{p_{i}(z), i\ge0\} $, 这里$ {\rm d}F(z) $是$ V_{z} $上的密度函数. 此外, 对于B.3(a)里的$ \delta>0 $, 或者(i)当$ j\to\infty $时$ E|p_{j}(z_{1}) |^{2(2+\delta)} =O(j) $成立或者(ii) $ \sup_{j\ge 0}E |p_{j}(z_{1})|^{2(2+\delta)} <\infty $.

(c) 存在信息流序列$ \mathcal{F}_{n, t} $使得$ (e_{t}, \mathcal{F}_{n, t}) $成为一个鞅差序列, 且$ (z_{t}, x_{t}) $适应于$ \mathcal{F}_{n, t-1} $. 另外, 假定$ E(e_{t}^{2}|\mathcal{F}_{n, t-1}) =\sigma^{2}(t/n) $依概率1成立(a.s.), 其中$ \sigma^{2}(\cdot) $是正的在$ [0, 1] $上连续的函数, 并且有$ \max_{1\leq t\leq n}E(|e_{t}|^{q_{2}}| \mathcal{F}_{n, t-1}) <\infty $, $ q_{2}\geq4 $.

条件(a)考虑了两种情况$ z_t $. 在(i)里, $ z_t $是一个严格平稳$ \alpha $-混合过程(参见Gao (2007)), 与$ x_t $独立, 而在(ii)里, $ z_t $与$ x_t $相关, 因为都含有$ \epsilon_{t}, \cdots, \epsilon_{t-d+1} $. 这两种情况有区别但也有交集, 因为$ z_t $在(ii)是$ d $-相依序列, 属于$ \alpha $-混合过程的一个子类, 但是就与$ x_t $的关系而言, (i)和(ii)相互排斥. 当然, $ x_t $和$ z_t $相关性的存在对理论结果的建立具有挑战性, 克服这些困难的技术路线请参考Dong and Linton (2018)中引理A.1$ \sim $A.3.

条件(b)是关于支撑集$ V $($ \equiv V_{z} $, 以下均做此简化)上的正交函数序列, 其线性组合可以逼近未知回归函数$ g(\cdot) $. 如果$ V=\mathbb{R} $, 我们可以选择密度函数$ {\rm d}F(z)=(2\pi)^{-1/2}{\rm e}^{-z^{2}/2} {\rm d}z $和厄尔米特正交系; 如果$ V=[0, \infty) $, 我们可以选择$ {\rm d}F(z)={\rm e}^{-z}{\rm d}z $和拉盖尔正交系; 如果$ V $为有限紧区间, 我们可以选择切比雪夫, 勒让德多项式系, 或者三角函数正交系.

条件(c)是在文献里广为采用的鞅差序列, 参见Park and Phillips (1999, 2001), Gao and Phillips (2013). 但是, 条件(c) 允许异方差存在, 而异方差函数依赖于时间变量$ t/n $, 使得理论结果具有广泛的应用范围. 更一般地, 条件方差$ \sigma^{2}(\cdot) $可以是多元的, 除随机变量外, 还可以以$ z_{t} $或者$ x_{t} $甚至二者为变量. 这种可能性只影响条件方差矩阵, 而主要的理论结果仍然成立. 为简单起见, 我们不在这里讨论这种可能性.

估计程序  我们采用正交级数逼近和最小二乘法来估计所有未知函数, 根据这些函数的特点和在回归方程里所起的作用, 它们属于不同的函数空间.

首先, 假设$ \beta(\cdot)\in L^{2}[0, 1] $. 令$ \varphi_{0}(r)\equiv1 $, 而对于$ j\geq1 $, $ \varphi_{j}(r)=\sqrt{2}\cos(\pi jr) $. 那么, $ \{\varphi_{j}(r)\} $是$ L^{2}[0, 1] $的标准正交基, 满足$ \langle \varphi_{i}(r), \varphi_{j}(r) \rangle =\int_0^1\varphi_{i}(r)\varphi_{j}(r){\rm d}r=\delta_{ij} $. 于是,

(55) $ \begin{equation} \beta(r)=\sum\limits_{j=0}^{\infty}c_{1, j}\varphi_{j}(r), \quad\text{其中} \ c_{1, j}=\langle\beta(r), \varphi_{j}(r)\rangle. \end{equation} $

其次, 假设$ g(\cdot)\in L^{2}(V, {\rm d}F(x)) $. 根据假设B.3, $ \{p_{j}(x), j\ge0\} $是$ L^{2}(V, {\rm d}F(x)) $的标准正交基, 其内积为$ \langle q_{1}, q_{2}\rangle= \int_{V} q_{1}(x)q_{2}(x){\rm d}F(x) $. 因此, 未知函数$ g(x) $有正交级数展开,

(56) $ \begin{equation} g(x)= \sum\limits_{j=0}^{\infty}c_{2, j} p_{j}(x), \quad\text{其中}\ c_{2, j}= \langle g(x), p_{j}(x)\rangle. \end{equation} $

最后, 因为$ x_{t}=O_{P}(\sqrt{t}) $, 未知函数$ m(\cdot) $的支撑集为$ \mathbb{R} $. 假设$ m(\cdot)\in L^{2}(\mathbb{R}) $, 空间里的内积为$ \langle f_{1}, f_{2}\rangle=\int f_{1}(x)f_{2}(x){\rm d}x $, 标准正交基为厄尔米特函数系$ \{\mathscr{H}_{j}(x)\} $. 我们有$ m(x) $的正交级数展开,

(57) $ \begin{equation} m(x)= \sum\limits_{j=0}^{\infty}c_{3, j} \mathscr{H}_{j}(x), \ \text{其中}\ c_{3, j}= \langle m(x), \mathscr{H}_{j}(x) \rangle. \end{equation} $

取正整数$ k_{i} $, $ i=1, 2, 3 $. 定义$ \beta(r) $级数展开的部分和$ \beta_{k_{1}}(r)= \sum_{j=1}^{k_{1}} c_{1, j}\varphi_{j}(r) $和余项$ \gamma_{1k_{1}}(r) = \sum_{j=k_{1}+1}^{\infty}c_{1, j} \varphi_{j}(r) $. 熟知, 如果$ \beta(r) $光滑, 当$ k_{1}\rightarrow \infty $时, 逐点收敛$ \beta_{k_{1}}(r) \rightarrow \beta(r) $成立. 类似地, 定义部分和$ g_{k_{2}}(x) =\sum_{j=0}^{k_{2}-1} c_{2, j}p_{j}(x) $和余项$ \gamma_{2k_{2}}(x)= \sum_{j=k_{2}}^{\infty} c_{2, j}p_{j}(x) $; 部分和$ m_{k_{3}}(x)= \sum_{j=0}^{k_{3}-1}c_{3, j} \mathscr{H}_{j}(x) $和余项$ \gamma_{3k_{3}}(x)= \sum_{j=k_{3}}^{\infty}c_{3, j}\mathscr{H}_{j}(x) $. 它们都具有相应的收敛性$ g_{k_{2}}(x) \rightarrow g(x) $和$ m_{k_{3}}(x)\rightarrow m(x) $当$ k_{2}, k_{3}\rightarrow \infty $. 具体的收敛结果见Dong, Gao and Tjøstheim (2016), Dong and Linton (2018), Dong, Linton and Peng (2021).

记$ c_{i}= (c_{i, 0}, \cdots, c_{i, k_{i}-1})^\top $, $ i=1, 2, 3 $, $ \phi_{k_{1}}(r)=(\varphi_{1}(r), \cdots, \varphi_{k_{1}}(r))^\top $, $ a_{k_{2}}(x)=(p_{0}(x), \cdots, p_{k_{2}-1}(x))^\top $, $ b_{k_{3}}(x)= (\mathscr{H}_{0}(x), \cdots, \mathscr{H}_{k_{3}-1} (x))^\top $. 因此, $ \beta_{k_{1}}(r)= \phi_{k_{1}} (r)^\top c_{1} $, $ g_{k_{2}}(x)=a_{k_{2}}(x)^\top c_{2} $, $ m_{k_{3}}(x)=b_{k_{3}}(x)^\top c_{3} $. 模型(54)可以写为:

(58) $ \begin{equation} \begin{split} y_{t}= & \phi_{k_{1}}(t/n)^\top c_{1}+a_{k_{2}}(z_{t})^\top c_{2}+ b_{k_{3}}(x_{t})^\top c_{3}+\\ & \gamma_{1k_{1}}(t/n)+\gamma_{2k_{2}}(z_{t})+\gamma_{3k_{3}}(x_{t})+e_{t}, \end{split} \end{equation} $

$ t=1, \cdots, n $.

要把方程组(58)写成矩阵形式, 令$ y=(y_{1}, \cdots, y_{n})^\top $, $ c=(c_{1}^\top, c_{2}^\top, c_{3}^\top)^\top $, $ e=(e_{1}, \cdots, e_{n})^\top $, $ \gamma=(\gamma(1), \cdots, \gamma(n))^\top $这里$ \gamma(t)= \gamma_{1k_{1}}(t/n) +\gamma_{2k_{2}}(z_{t})+ \gamma_{3k_{3}}(x_{t}) $, $ t=1, \cdots, n $,

$ B_{nk}= \begin{pmatrix} \phi_{k_{1}}(1/n)^\top & a_{k_{2}}(z_{1})^\top & b_{k_{3}} (x_{1})^\top\\ \vdots & \vdots & \vdots\\ \phi_{k_{1}}(1)^\top & a_{k_{2}}(z_{n})^\top & b_{k_{3}}(x_{n})^\top \end{pmatrix}. $

它是$ n\times k $矩阵, $ k=k_{1}+k_{2}+k_{3} $. 从而,

(59) $ \begin{equation} y=B_{nk}c+\gamma+e. \end{equation} $

那么由最小二乘法可得$ \widehat{c}=(\widehat{c}_{1}^\top, \widehat{c}_{2}^\top, \widehat{c}_ {3}^\top)^\top=(B_{nk}^\top B_{nk})^{-1}B_{nk}^\top y $, 如果$ B_{nk}^\top B_{nk} $非奇异(大概率是这样的).

对于任意$ r\in [0, 1] $, $ z\in V $和$ x\in\mathbb{R} $, 定义$ \widehat{\beta}_{n}(r)=\phi_{k_{1}}(r)^\top \widehat{c}_{1} $, $ \widehat{g}_{n}(z)=a_{k_{2}}(z)^\top \widehat{c}_{2} $和$ \widehat{m}_{n}(x)=b_{k_{3}}(x)^\top \widehat{c}_{3} $分别为未知函数$ \beta(r), g(z) $和$ m(x) $的估计量,

(60) $ \begin{equation} (\widehat{\beta}_{n}(r), \widehat{g}_{n}(z), \widehat{m}_{n}(x))^\top =\Psi(r, z, x)^\top\widehat{c}, \end{equation} $

其中$ \Psi(r, z, x) $是分块矩阵,

(61) $ \begin{equation} \Psi(r, z, x)= \begin{pmatrix} \phi_{k_{1}}(r) & \bf{0} & \bf{0}\\ \bf{0} & a_{k_{2}}(z) & \bf{0}\\ \bf{0} & \bf{0} & b_{k_{3}}(x) \end{pmatrix}, \end{equation} $

这里0是零列向量, 在不同的行维数不同.

渐近理论  在介绍极限理论之前我们需要下面的假设.

假设C.3

(a) 设函数$ \beta(\cdot) $, $ g(\cdot) $和$ m(\cdot) $分别为$ s_{1} $, $ s_{2} $和$ s_{3} $阶连续可微, 且$ \beta^{(s_{1})}(\cdot) $, $ g^{(s_{2})}(\cdot) $和$ m^{(s_{3})}(\cdot) $仍然属于原希尔伯特函数空间.

(b) 对于$ \beta(\cdot) $函数, 设$ \int_{0}^{1}\beta(r){\rm d}r=0 $.

因为我们不仅需要正交级数的收敛性还需要一定的收敛速度, 所以这个假设要求未知函数具有一定的光滑性. 至于$ s_{i} $的具体要求, 我们将结合样本容量和截断参数在下面给出. 条件(b)是识别性条件, 因为$ \beta(\cdot) $和$ g(\cdot) $的级数展开都可能含有常数项, 所以这个条件能保证识别此常数.

假设D.3  所有$ k_{i} $, $ i=1, 2, 3 $, 均随$ n $发散, 且满足

(a) 如果B.3.(b) (i)成立, 1) $ k_{2}^{2+2/(2+\delta)}=o(n) $, $ k_{3}^{5}=o(n) $, 2) $ k_{1}k_{2}^{1+1/(2+\delta)}=o(n) $, $ k_{1}^{2}k_{3}^{3}=o(n) $, $ k_{2} ^{2}k_{3}^{3/2}=o(n) $; 如果B.3.(b) (ii)成立, 3) $ k_{2}^{2}=o(n) $, $ k_{3}^{5} =o(n) $, 4) $ k_{1}k_{2}=o(n) $, $ k_{1}^{2}k_{3}^{3}=o(n) $, $ k_{2}^{3}k_{3} ^{3}=o(n) $.

(b) 假设当$ n\to\infty $时, 5) $ nk_{1}^{-(2s_{1}-1)}=o(1) $, $ nk_{2}^{-(s_{2}-1)}=o(1) $, $ n^{1/2}k_{3}^{-(s_{3}-1)} =o(1) $; 6) $ nk_{2}k_{1}^{-2s_{1}}=o(1) $, $ nk_{3}k_{1}^{-2s_{1}}=o(1) $, $ nk_{1} k_{2}^{-s_{2}}=o(1) $, $ nk_{3}k_{2}^{-s_{2}}=o(1) $, $ n^{1/2}k_{1}k_{3}^{-s_{3}}=o(1) $, $ n^{1/2}k_{2}k_{3}^{-s_{3}} =o(1) $.

这里D.3的条件对截断参数$ k_{i} $, $ i=1, 2, 3 $, 提出了要求, 保证了估计量的收敛性. 由于在B.3.(b) (i)里$ p_{j}(z_{1}) $的矩随着$ j $发散, 在1)和2)里$ k_{2} $条件比3)和4) 里苛刻一些; 因为$ x_{t} $的非平稳性, $ k_{3} $发散的很慢, 其发散的阶与文献Dong, Gao and Tjøstheim (2016)类似, 而那里回归变量仅仅是单整向量. 如果简单地取$ k_{i}=\tilde{k} $, $ i=1, 2, 3 $, 那么$ \tilde{k}^{6}=o(n) $满足假设.

此外, 条件2)和4)是针对三个$ k_{i} $的任意两个, 而条件1)和3)是针对每个$ k_{2} $和$ k_{3} $, 这是由对称分块矩阵$ B_{nk}^{\top}B_{nk}: =(\Pi_{ij})_{3\times3} $的结构引起的. 条件2)和4)是分别在B.3.(b) (i)和B.3.(b) (ii) 下针对子块$ \Pi_{12}=\sum_{t=1}^{n}\phi_{k_{1}}(t/n) a_{k_{2}} (z_{t})^{\top} $提出的. 更重要的是, $ k_{1} $没有出现在条件1)和3). 这是因为$ \Pi_{11}:=\sum_{t=1}^{n}\phi_{k_{1}}(t/n) \phi_{k_{1}} (t/n)^{\top} $收敛的很快, 所以关于$ k_{1} $的条件被收敛较慢的$ \Pi_{12} $和$ \Pi_{13} $的条件所取代.

给定假设C.3里的光滑性, 条件D.3.(b)要求导数的阶足够高, 使得余项($ \gamma_{ik_{i}} $, $ i=1, 2, 3 $)收敛到零的速度非常快, 从而我们的估计量是渐近无偏的. 这个条件在文献里(见Belloni et al. (2015)里Comment 4.3)称为过度光滑(under-smoothing)条件. 综合假设D.3里所有关于$ k_{i} $的条件可知, 我们对光滑度有一个最低要求, 并且它们之间是相容的, 比如在极端情况下$ k_{i}=[n^{\tau}] $, $ i=1, 2, 3 $, $ 0<\tau<1/5 $, $ s_{1}\geq3 $, $ s_{2}\geq6 $和$ s_{3}\geq4 $, 该假设得到满足.

记对角$ k\times k $矩阵$ D_{n}=\mathrm{diag}(\sqrt{n}I_{k_{1}}, \sqrt{n}I_{k_{2}}, \sqrt{n/d_{n}}I_{k_{3}}) $ ($ k=k_{1}+k_{2}+k_{3} $), 对角分块矩阵$ U_{k}=\mathrm{diag}(I_{k_{1}}, U_{k_{2}}, L_{W}(1, 0)I_{k_{3}}) $, 其中$ U_{k_{2}}=E[a_{k_{2}}(z_{1}) a_{k_{2}}(z_{1})^{\top}] $, $ L_{W}(1, 0) $是布朗运动$ W(r) $的局部时, 对角分块矩阵$ V_{k}=\text{diag}(V_{\ast}, \int_{0}^{1} \sigma^{2}(r) {\rm d}L_{W}(r, 0)I_{k_{3}}) $, 这里$ V_{\ast}=(V_{\ast ij}) $是$ 2\times2 $对称分块矩阵,

$ \begin{align*} V_{\ast11}= & \int_{0}^{1} \phi_{k_{1}}(r)\phi_{k_{1}}(r)^{\top} \sigma^{2}(r){\rm d}r, \\ V_{\ast12}= & \int_{0}^{1}\phi_{k_{1}}(r)\sigma^{2}(r){\rm d}r\, E (a_{k_{2}}(z_{1})^{\top}), \\ V_{\ast22}= & \int_{0}^{1} \sigma^{2}(r){\rm d}r\, E(a_{k_{2}}(z_{1}) a_{k_{2}}(z_{1})^{\top}). \end{align*} $

在同方差情形下, $ V_{k}=\sigma^{2}U_{k}, $这里$ \sigma^{2}(\cdot)\equiv \sigma^{2} $. 另外, 记$ \overline{\Psi} (r, z, x) $为$ \Psi(r, z, x) $的标准化矩阵, 也就是对$ \Psi(r, z, x) $右乘$ \text{diag} (\|\phi_{k_{1}}(r)\|, \|a_{k_{2}}(z)\|, \|b_{k_{3}}(x)\|)^{-1} $使其中的向量成为单位向量, $ \bar{U}_{k}=\mathrm{diag}(I_{k_{1}}, U_{k_{2}}, I_{k_{3}}) $, $ \bar{V}_{k}=\text{diag}(V_{\ast}, I_{k_{3}}) $.

定理3.11  设$ U_{k_{2}} $和$ V_{\ast} $的所有特征值下界大于零而上界小于无穷对于所有$ n $一致成立, 并且假设A.3$ \sim $D.3成立. 那么, 对任意$ r\in[0, 1] $, $ z\in V $和$ x\in\mathbb{R} $, 当$ n\to\infty $,

(62) $ \begin{align} \Omega_{n}^{-1/2} \begin{pmatrix} \frac{\sqrt{n}}{\|\phi_{k_{1}}(r)\|}[\widehat{\beta}_{n}(r)-\beta(r)]\\ \frac{\sqrt{n}}{\|a_{k_{2}}(z)\|}[\widehat{g}_{n}(z)-g(z)]\\ \sqrt{\frac{n}{d_{n}}}\frac{1}{\|b_{k_{3}}(x)\|}[\widehat{m}_{n}(x)-m(x)] \end{pmatrix} \to_{D}N\left(\bf{0}, \begin{pmatrix} 1 & 0 & 0\\ 0& 1 &0 \\ 0& 0 & a^{2} \end{pmatrix} \right), \end{align} $

其中$ \Omega_{n}:=\overline{\Psi}(r, z, x)^{\top} \bar{U}_{k}^{-1} \bar{V}_{k} \bar{U}_{k}^{-1} \overline{\Psi}(r, z, x) $是$ 3\times3 $矩阵, $ a^{2}:=L_{W}^{-2}(1, 0)\int_{0}^{1}\sigma^{2}(r){\rm d}L_{W}(r, 0) $, $ \bf{0} $是3维零列向量.

矩阵$ U_{k_{2}} $和$ V_{\ast} $的特征根的有界性在文献里广为采用. 参见Belloni et al. (2015)里条件A.2和Hansen (2015)里假设1.3和1.4. 鉴于$ U_k $和$ V_k $结构, 这个条件是推断正态性的充分条件, 因为$ L_{W}(1, 0)=O_{P}(1) $意味着, 对于任意$ \epsilon>0 $, 存在常数$ M>0 $使得$ P(M^{-1}\le L_{W}(1, 0)\le M)\ge1-\epsilon $ (从而$ L_{W}^{-1}(1, 0)=O_{P}(1) $亦成立). 这一点很容易验证, 因为$ L_{W}(1, 0) $具有分布函数$ 2\Phi(x)-1 $, 其中$ \Phi(x) $为标准正态分布函数.

在同方差情形$ V_{k}=\sigma^{2}U_{k} $, 对于$ U_{k_{2}} $和$ V_{\ast} $的要求条件退化为对$ U_{k_{2}} $的要求条件, 研究者往往通过标准化将$ U_{k_{2}} $转换为单位矩阵. 见Chen and Christensen $ (2015, {\rm p}450) $里方程(11)和Belloni et al. $ (2015, {\rm p}347) $. 由于单位根$ x_{t} $过程的发散性和$ m(x) $的可积性, $ m(x_{t}) $和所有$ \beta(t/n) $和$ g(z_{t}) $的交互作用都渐近为零, 从而$ \Omega_{n} $具有对角分块矩阵的形式.

因此, 我们可以将$ \widehat{m}_{n}(x) $的极限与其他估计量的极限区分开来, 即当$ n\rightarrow \infty $时,

(63) $ \begin{eqnarray} &&[\overline{\Psi}_{12}(r, z)^{^{\intercal}}U_{\ast}^{-1}V_{\ast}U_{\ast}^{-1} \overline{\Psi}_{1}(r, z)]^{-1/2} \begin{pmatrix} \frac{\sqrt{n}}{\|\phi_{k_{1}}(r)\|}[\widehat{\beta}_{n}(r)-\beta(r)]\\ \frac{\sqrt{n}}{\|a_{k_{2}}(z)\|}[\widehat{g}_{n}(z)-g(z)] \end{pmatrix} \rightarrow_{D} N(0, I_{2}), \end{eqnarray} $

(64) $ \begin{eqnarray} &&\sqrt{\frac{n}{d_{n}}}\frac{1}{\Vert b_{k_{3}}(x)\Vert}(\widehat{m}_{n} (x)-m(x))\rightarrow_{D} N(0, a^{2}). \end{eqnarray} $

这些结果与现有文献均有可比性. 注意到关于$ U_{k_{2}} $和$ V_{\ast} $特征根的条件, 极限(63)里$ \widehat{\beta}_{n}(r)-\beta(r) $和$ \widehat{g}_{n}(z)-g(z) $的收敛速度分别为$ [\sqrt{n}/\Vert\phi_{k_{1}}(r)\Vert]^{-1} $和$ [\sqrt{n}/\Vert a_{k_{2}}(z)\Vert]^{-1} $, 与Newey (1997)里定理2及Chen and Christensen (2015)里定理3.1均一致. 另一方面, 极限(64)的收敛速度与Dong, Gao and Tjøstheim (2016)里定理3.3一致. 总的来说, 虽然可加非参数模型具有不同性质的协变量, 但是所有估计量具有各自独有的收敛速度.

更重要的是, 我们可以为$ \|\widehat{\beta}_{n}(r)-\beta(r)\| $和$ \|\widehat{g}_{n}(z)-g(z)\| $建立传统的非参数最优收敛速度, 这里$ \|\cdot\| $是函数空间的模, 而经典的最优速度是指文章Stone (1982, 1985)里所建立的速度.

推论3.3  假设A.3$ \sim $D.3成立. 当$ n\to\infty $时对模型(54)的估计量我们有$ \|\widehat{\beta}_{n}(r)-\beta(r)\|=O_{P}(\sqrt{k_{1}/n} +k_{1}^{-s_{1}}) $, $ \|\widehat{g}_{n}(z)-g(z)\| =O_{P}(\sqrt{k_{2}/n} +k_{2}^{-s_{2}}) $和$ \|\widehat{m}_{n}(x)-m(x)\| =O_{P}(\sqrt{k_{3} }/\sqrt[4]{n}+k_{3}^{-s_{3}/2}) $同时成立.

确实, 如果$ k_{i}=O(n^{1/(2s_{i}+1)}) $, 那么前两个估计量的收敛速度为$ O_{P}(n^{-s_{i}/(2s_{i}+1)}) $, $ i=1, 2 $, 这正是Stone (1982, 1985)所建立的最优速率. 就我们所知, 文献里迄今为止没有关于单位根过程非参数估计量的所谓最优速率. 虽然Newey (1997), Chen and Christensen (2015, p451)在相同的情形下得到筛分法的最优速率, 我们的推论在可加模型里为两个非参数函数的估计量建立了联合最优速率.

如果要做统计推断, 那么未知函数$ \sigma^{2}(\cdot) $需要估计. 这个函数的估计有可能从误差项的估计里得到, 但是我们在这里并不打算做任何进一步的讨论, 因为这可能偏离了文章的初衷. 请参考Dong and Linton (2018, p219)里关于同方差情形下$ \sigma^{2} $的估计.

实证研究  令$ Y_{t} $表示可口可乐对数调整收盘价格, $ X_{t} $表示百事可乐对数调整收盘价格, 令$ z_{t} $表示可口可乐交易量与二者成交量之和的比率, 所以$ 0\leq z_{t}\leq1 $. 时间跨度为1972年6月1日到2016年8月31日. 除去所有周末和节假日, 我们有$ n=11163 $观测值. 图 1和2分别绘出了$ Y_{t} $, $ X_{t} $和$ z_{t} $.

为了验证$ X_{t} $是否为单位根过程, 我们采用ADF检验. 检验的$ p $-值为0.9901, 不能拒绝$ X_{t} $具有单位根. 对于$ Y_{t} $检验的$ p $-值为0.9627, 同样不能拒绝它为单位根过程. 为了从视觉上感受两个单位根过程, 图 3绘出了它们的日回报过程.边际价格过程看起来包含漂移项和非常返性, 我们假设$ X_{t}=\mu_{1}+X_{t-1}+\xi_{t} $和$ Y_{t}=\mu_{2}+Y_{t-1}+\zeta_{t} $, $ \mu_{1}, \mu_{2}\neq0 $. 因此, $ X_{t}-\mu_{1}t=X_{0}+ \sum_{j=1}^{t} \xi_{j} $和$ Y_{t}-\mu_{2}t=Y_{0}+\sum_{j=1}^{t}\zeta_{j} $满足理论条件. 令$ x_{t}=X_{t}-\hat{\mu}_{1}t $和$ y_{t}=Y_{t}-\hat{\mu}_{2}t $, 其中$ \hat{\mu}_{1}=(X_{n}-X_{0})/n $和$ \hat{\mu}_{2}=(Y_{n}-Y_{0})/n $分别是$ \mu_{1} $和$ \mu_{2} $的相合估计. 更重要的是, $ z_t $和$ x_t $有可能是相关的, 我们的理论恰好可以处理这种情形.

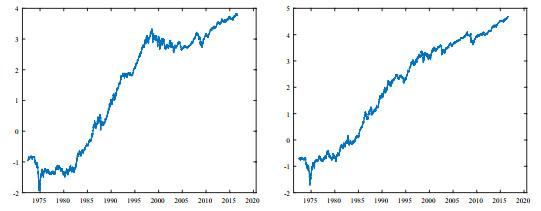
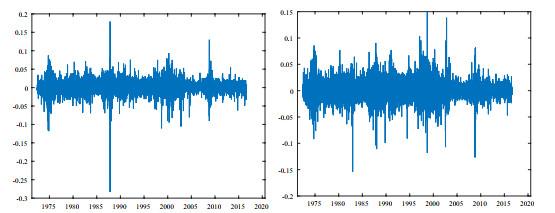
我们将通过下列模型来考察$ y_{t} $, $ t/n $, $ z_{t} $和$ x_{t} $的关系,

(65) $ \begin{align} y_{t}=\beta(t/n)+g(z_{t})+m(x_{t})+e_{t}, \end{align} $

$ t=1, \cdots, n $, 其中所有函数$ \beta(\cdot) $, $ g(\cdot) $和$ m(\cdot) $均未知, 待估.

因为函数$ \beta(\cdot) $和$ g(\cdot) $定义于$ [0, 1] $, 我们使用余弦函数系对它们正交展开, 而对于$ m(\cdot) $我们采用厄尔米特函数系正交展开.

在实证中级数估计的一个关键问题是确定截断参数, 只有当它们确定后, 估计程序才能够进行. 然而, 截断参数的选择并没有理论可循, 尤其是在模型里既包括平稳过程又包括单整过程的情形. 因为预测能力是金融模型的重要特征, 我们将以预测能力为标准来决定截断参数.

模型的预测能力就是所谓样本外均方误差(out-of-sample mse). 对于给定的$ k_{i} $$ (i=1, 2, 3) $, 我们用一部分数据, 比方说$ 1\leq t\leq n_{1} $ ($ n_{1}<n $), 来预测模型, 然后用估计的模型来预测被解释变量在$ t=n_{1}+1 $处的值, 得到$ \widehat{y}_{n_{1}+1} $. 在给定$ k_{i} $, 样本外均方误差定义为$ J^{-1}\sum_{j=1}^{J}(\widehat{y}_{n_{j}+1}-y_{n_{j}+1})^{2} $, 其中$ n_{j}<n_{j+1}<n $, $ j=1, \cdots, J-1 $. 具有较小的样本外均方误差的模型(截断参数)就被认为有较好的预测能力.

在此实证分析中, 取$ J=20 $, $ n_{j}=9162+100j $, $ 1\leq j\leq J $. 考虑到函数$ \beta(\cdot) $和$ g(\cdot) $里数据的相似性, 我们令$ k_{1}=k_{2} $为二者的截断, 而$ m(\cdot) $的截断记为$ k_{3} $. 对所有可行的$ k_{i} $ (可行是从模型复杂性而言)计算样本外均方误差, 结果见表 12.

从表中可以看到$ \widehat{k}_{1}=\widehat{k}_{2}=2 $和$ \widehat{k}_{3}=1 $对应的模型具有最小样本外均方误差, 即最佳预测能力. 因此, 就这组数据而言, 我们推荐模型(65)里的函数分别为$ \widehat{\beta}(r)=\beta_{2}(r) $, $ \widehat{g}(z)=g_{2}(z) $和$ \widehat{m}(x)=m_{1}(r) $. 估计后, 我们得,