为了评估或评价培训计划和实施政治或社会或者经济政策或事件对结果的影响, 人们需要估计其处置效应treatment effect (或者处理效应), 这在经济、金融等许多应用领域都引起了极大的兴趣和关注, 在估计处置效应的过程中, 往往需要高级计量经济学知识或统计分析工具.估计处置效应的难度在于没有处置的单元的结果未被直接观测到, 通常称为反事实(counterfactual).为了克服这一困难, 已有文献中提出了许多方法, 如回归调整、匹配、逆概率(倾向得分函数, propensity score function)加权、双重差分(difference-in-differences, DiD)、断点回归方法等等, 来估计平均处置效应(ATE)和分位数处置效应(QTE).然而, 上述方法大多依赖于估计倾向得分函数, 比如, 关于横截面数据可参考Imbens and Wooldridge (2009)的文章, 时间序列数据可参考Liu, Cai and Fang et al. (2020)的综述文章, QTE方面可参考Tang (2020)的综述文献, 更多细节的内容可见参考书Cerulli (2015).

在上述的解决处置效应的计量经济学方法中, 在应用中, 比较流行的方法是经典DiD方法, 被要求有两个时间段(处置前后)和两组(处置组和对照组)的情况下.并且如果平行趋势假设成立, 那么处置组的ATE可以简单地通过处置组的平均结果随时间的变化和对照组的平均结果随时间的变化的差异来估计.众所周知, DiD类型方法避免估计倾向得分函数, 以避免倾向得分函数可能的错误假设.因此, 对于大面板数据, Hsiao, Ching and Wan (2012) (以下简称为HCW)把经典的DiD方法做了创造性拓展, 可以用来处理大面板数据, 称为HCW方法.

事实上, HCW提出了一个基于因子模型来估计面板数据的平均处置效应.与面板数据的经典DiD方法不同, HCW考虑了具有多个单元和多个时间段的面板数据, 其中处置发生在特定时间和之后.他们的重点是通过将其他单位作为对照组来观测特定单位的处置效应.如果HCW的面板数据的横截面截面和时间序列的维度较大, 可以采用Bai and Ng (2002), Pesaran (2006), Bai (2009)等方法来估计影响因子.然而, 在许多应用中, 研究者经常遇到维度不大的情况.针对这一问题, HCW提出了一种不考虑因子的反事实结果估计方法.在某些简单假设条件下, HCW证明了利用普通最小二乘回归仍然可以得到其估计量, 从而使计算变得简单.此外, 正如Li and Bell (2017)所指出的, HCW中的方法优点之一是不需要假设没有样本选择效应.换句话说, 它绕过了虚拟处置和结果之间的相关性问题.此外, 它不要求处置单位和控制单位在没有处置的时间遵循平行路径.

近年来, 研究人员从理论和实证的角度对HCW的研究方法进行了广泛的拓展和应用.例如, 首先, 通过应用HCW的方法, Chen, Han and Li et al. (2013)构建现货市场波动率的反事实以及主要基于中国与国际股票市场的横截面相关性, 研究了引入沪深300 (CSI300)¹指数期货交易对中国股市现货价格波动率(VIX)的影响.其次, Bai, Li and Ouyang (2014)将HCW的方法扩展到相关的时间系列是非平稳单位根过程的情况, 然后, 探讨房产税对房价的影响, 利用2011年1月开始在上海和重庆进行的房产税政策试验, 并利用其他省市的房价, 采用HCW的方法估计上海和重庆在不征收房产税的情况下的假设房价.第三, Ouyang and Peng (2015)放宽了HCW中的线性回归函数假设, 允许存在非参数回归函数, 并将HCW模型推广到半参数设置, 并以此方法研究2008年中国的经济刺激方案.第四, Du and Zhang (2015)建议使用"多个剔除交叉验证"(leave-many-out cross validation)准则代替HCW中的Akaike信息准则(AIC)来选择最优控制单元, 并将其应用于对中国的购房限制、房产税和房价的反事实分析.此外, Ke, Chen and Hong et al. (2017)利用1990年到2013年中国地级市数据, 通过在没有高铁项目的情况下利用选定的非高铁城市的结果, 构建高铁城市人均实际GDP的假设反事实, 评估了高铁项目对目标城市节点(高铁城市)经济增长的影响.此外, Li and Bell (2017)认为HCW的方法可以在限制性较小的假设下仍然是有效, 实际上, Li and Bell (2017)去掉了HCW中施加的一些假设, 然后导出了HCW平均处置效应估计量的渐近性质.另外, Li and Bell (2017)将最小绝对收缩和选择算子(least absolute shjrinkage and selection operator, LASSO)方法引入HCW的方法中使得控制元选择在横截面尺寸很大的情况下更加有效, 而Carvalho, Masini and Medeiros (2018)证明了LASSO估计量是相合的并且渐近正态分布的.更重要的是, Carvalho et al. (2018)将HCW的方法推广为一种灵活且易于实施的方法, 称为ArCo, 用于在没有对照组的情况下, 估计干预对单个处置单元的因果效应, 这与文献中之前的建议一致, 此外, 他们还考虑了多种干预措施和受污染效应的测试.最后, Carvalho et al. (2018)应用他们的模型评估了2007年巴西实施的反逃税计划对通货膨胀和其他宏观经济变量(比如:经济增长、零售和信贷)的影响.

¹沪深300指数是一个市值加权的股市指数, 旨在复制在上海和深圳交易所交易的前300只股票的表现.

最近, 为了利用面板数据或纵向数据(longitudinal data)进行因果推断, 以捕捉异质处置效应, 双因素线性固定效应回归(two-way linear fixed effect, 记为2FE)已成为面板数据估计因果效应的默认方法.使用2FE估计量的主要目的是同时调整未观测到的特定单位和/或特定群体和/或特定时间的混杂因素.事实上, 根据De Chaisemartin and D'Haultfoeuille (2020)的一项调查, 在2010年至2012年期间, 顶尖经济学杂志《美国经济评论》发表的所有实证文章中, 有19%使用了双因素固定效应回归来估计处置对结果的影响.例如, 为了估计ATE, Imai and Kim (2019, 2020)提出了与2FE模型匹配的方法, 以捕获未观测到的特定单位和特定时间的混杂因素, 而De Chaisemartin and D'Haultfoeuille (2020)提出了另外一种新的估计方法, 以适应未观测到的特定群体和特定时间的混杂因素.最后, Sun and Abraham (2020)提出了一种替代方法来估计一个有趣处置的动态效应, 而不是包括处置的领先和滞后的双向固定效应回归, 当平行趋势假设只有在观测到的协变量的条件作用下才可能成立时, Callaway and Sant'Anna (2020)表明, 即使观测到的特征的差异导致组间的非平行结果动态变化, 在交错DiD设置中也确定了一系列因果效应参数.根据他们的鉴定结果, 他们提出了不同的聚类方案, 可以用来突出不同维度的处置效应异质性, 并总结参与处置的整体效应.

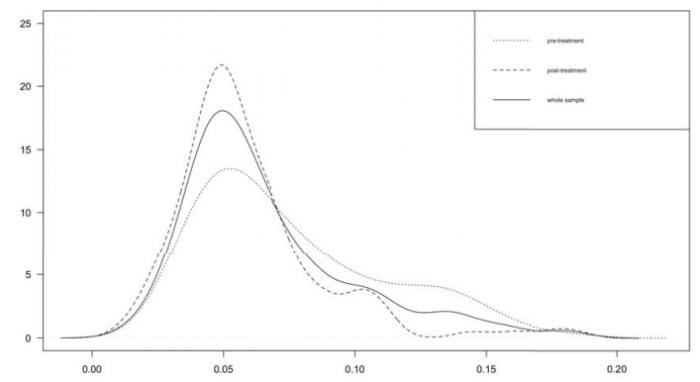
尽管ATE方法在应用很受欢迎, 但当潜在结果的真实分布是不对称或异质性或厚尾时, ATE可能不能很好地代表政策的效果.例如, 让我们观察Chen et al. (2013)所考虑的沪深300指数现货价格波动率在2002年1月至2020年10月的分布估计, 如图 1所示, 从图 1可以清楚地看到三个样本的密度分布:处置前(点线)、处置后(虚线)和整个样本(实线)的分布是不对称的, 并且是严重向右倾斜的.因此, ATE可能不适用于这个应用问题来刻画政策效应.相反, 我们需要考虑处置效应的分布影响.在文献中, 分位数处置效应(QTE)可以用来识别政策在对应于观测结果和反事实结果的整个分布的任何分位数上的效应.

然而, 关于用面板数据估计QTE的文献非常有限.大概, 最近的文献包括Callaway, Li and Oka (2018)以及Callaway and Li (2019), 他们考虑在Copula不变性的假设下(见后面的假设Q2), 在固定时间段(有限面板)的DiD设置下使用面板数据估计QTE (见后面的假设Q2), 以及Cai, Fang and Lin et al. (2021)的文章, 该文将HCW的方法推广到面板数据的QTE设置, 从而对大面板数据的处置效果进行了综合刻画和考察.估计反事实的分位数的处置单位, 不同于HCW的方法及其它的扩展, Cai et al. (2021)引入了条件累积分布函数(CDF)不变性的假设(见后面的假设Q3), 提出了一个简单的方法来使用条件CDF和无条件的CDF之间的关系.通过这种方法, 可以使用非参数和半参数方法来估计条件CDF.此外, Cai et al. (2021)导出了所提出的QTE估计量的大样本性质, 以及一种基于区块(blockwise) Bootstrap的易于实现的构造置信区间的方法.

最后, 使用QTE面板数据方法, Cai et al. (2021)通过分位数处置效果分析, 研究引入沪深300指数期货交易, 2010年4月16日由中国金融期货交易所正式推出, 是否对会现货市场波动率以及像Huang, Schlag and Shaliastovich et al. (2019)那样的波动率之波动率(volatility-in-volatility, VVIX)²产生影响.引入后, 有人批评引入指数期货交易可能会因过度投机而动摇现货市场, 也有人认为指数期货市场可以提高信息流的速度和质量, 使金融市场更加完善. Cai et al. (2021)的研究有趣发现是, 引入沪深300指数期货交易不仅对中国金融市场的VIX有显著影响, 而且对VVIX也有显著影响.

²波动率之波动率的定义可以在Huang et al. (2019)中找到.

本文的其余部分组织如下.第2节致力于回顾经典的DiD方法及其变体, 如用于估计多个时间段的ATE的双因素固定效应.第3节详细阐述了HCW的方法及其扩展, 第4节讨论了有限面板数据和大型面板数据的QTE估计.第5节是本文的结束语, 同时, 讨论了一些非常有趣而且挑战性极强的未来研究问题, 尤其和机器学习相关的未来研究方向.

首先, 让我回顾一下经典的DiD方法, 尽管它在计量经济学文献中众所周知, 例如, 见Cerulli (2015).事实上, 经典的DiD需要从一个实验组和一个控制组在两个或两个以上不同时期(比如, $ T $个时期, 且$ T\ge 2 $)测量的数据, 具体来说, 处置前至少一个时间段, 处置后至少一个时间段.为了评估一个项目或处置对一个个体群组的结果的影响, 通常假设有两组处置状态$ D = 0 $或$ 1 $, 其中$ 0 $表示未接受处置的个体, 即对照组, $ 1 $表示接受处置的个体, 即处置组.同时, 假设个体在两个时间段内被观测($ T = 2 $), $ t = 0 $和$ 1 $, $ 0 $表示处置组接受处置前的一段时间, 即处置前, $ 1 $表示处置组接受处置后的一段时间, 即处置后.每一次观测都以字母$ i = 1, \cdots, N $为指标, 每个个体通常有两个观测, 一个在处置前, 一个在处置后.为结果$ y_{it} $建模, 通常考虑以下回归模型

(1) $ \begin{equation} y_{it} = \beta_0 +\beta_1 D_i+\beta_2\, t+\Delta_{\rm DiD}(D_i\cdot t)+\varepsilon_i, \end{equation} $

其中系数是用希腊字母$ \{\beta_j\}_{j = 0}^2 $表示的, 还有$ \Delta_{\rm DiD} $也是未知参数, 以及$ \varepsilon_i $是一个随机未观测到的误差项.由(1)式, 我们可以清楚地看到, 系数有如下的解释: $ \beta_0 $是常数项, $ \beta_1 $表示处置组的特定效应(来解释处置和控制之间的平均永久性差异), $ \beta_2 $呈现控制组和处置组常见的时间趋势, $ \Delta_{\rm DiD} $是处置的真实效应.所以, DiD方法的重点在于估计$ \Delta_{\rm DiD} $.

为了估计$ \Delta_{\rm DiD} $, 从(1)式, 我们可以很容易地得到$ \Delta_{\rm DiD} = \left[E(y^1_1)-E(y^1_0)\right]-\left[E(y^0_1)-E(y^0_0)\right] $, 其中$ y^1_0 $和$ y^1_1 $分别是处置组处置前后的结果, $ y^0_0 $和$ y^0_1 $是对照组相应结果的样本平均数.因此, 差分-差分(或双重差分)估计值定义为处置组处置前后平均结果的差值减去对照组处置前后平均结果的差值, 这是一种差分中的差分, 定义为

(2) $ \begin{equation} \hat\Delta_{\rm DiD} = \left[\bar y^1_1-\bar y^1_0\right]-\left[\bar y^0_1-\bar y^0_0\right], \end{equation} $

其中$ \bar y^1_0 $和$ \bar y^1_1 $分别是处置组处置前后结果的样本平均数, $ \bar y^0_0 $和$ \bar y^0_1 $是对照组相应结果的样本平均数.我们可以很容易地证明$ \hat\Delta_{\rm DiD} $是$ \Delta_{\rm DiD} $的无偏和相合的估计.显然, 这个估计量可以被看作是两个前后估计量(pre-versus-post estimators)的差值, 即(2)右侧的第一部分, 减去对照组的估计量, 即(2)右侧的第二部分.当然, 上述设置可以很容易地推广到有$ T\ge 2 $但固定的情况, 更多细节读者可以参考Cerulli (2015).

值得一提的是, 最近, Henderson and Sperlich (2021)成功地把(2)推广到带有confounder (混杂变量)的非参数DiD情况, 也就是考虑处置效应函数$ \Delta_{\rm DiD}(x) $依赖于一些混杂变量$ x $, 然后利用非参数估计方法进行估计$ \Delta_{\rm DiD}(x) $, 同时, 利用他们的提出的模型来研究和评价美国著名的移民政策deferred action for childhood arrivals (DACA, "童年抵美者暂缓遣返")³对那些非法进入美国的小孩教育(中小学和高等)情况的影响.

³DACA, "童年抵美者暂缓遣返"计划, 是由奥巴马于2012年发起, 准许在年幼还没有决定权的时候跟着自己的父母或是一级亲属来到美国的人可以继续待在美国合法的工作跟生活, 不必被强硬地遣返回去自己的国家.但是必须每两年就重新续约一次这个协议

最后, 我深信国内学者对模型(1)有许多实证应用, 通常采用(2)式中的估计方法$ \hat\Delta_{\rm DiD} $.在此, 深表歉意的是, 由于篇幅有限, 没有对国内学者的中文文献进行综述.

近年来, 为了利用面板数据或纵向数据进行因果推断, 捕捉异质和动态的处置效应, 双因素线性固定效应回归已成为一种流行的方法, 用于从面板数据估计因果效应, 以调整未观测到的单位特定和/或群体特定和/或时间特定混杂因素.例如, 参见近期和新兴的关于DiD和/或事件研究中不同处置时间的异质处置效应的文献, 包括但不限于, Imai and Kim (2019, 2020), De Chaisemartin and D'Haultfoeuille (2020), Sun and Abraham (2020), Callaway and Sant'Anna (2020)以及其中的参考文献.实际上, Imai and Kim (2020)考虑了以下双因素线性固定效应回归模型

$ y_{it} = \alpha_i+\gamma_t+\beta^\top\, Z_{it}+\varepsilon_{it}. $

对于$ i = 1, 2, \cdots, N $以及$ t = 1, 2, \cdots, T $, 其中$ \alpha_i $和$ \gamma_t $分别是单位效应和时间固定效应, $ Z_{it} $是协变量, 然而Imai and Kim (2019)考虑了不带$ \gamma_t $项的上述模型.此外, Imai and Kim (2020)表明, 2FE模型同时对这两种未观测的混杂因素进行调整的能力严重依赖于线性可加效应的假设.使用2FE估计量的另一个常见理由是, 在两组和两个时间段的最简单设置下, 它与DiD估计量等价.此外, 他们认为, 在应用研究中通常遇到的更一般的情况下, 这种等效性并不存在.相反, 他们证明了多周期的DiD估计量等价于加权的2FE估计量, 但一些观测值的权重为负.因此, Imai and Kim (2020)将Imai and Kim (2019)中的单向固定效应回归估计量的匹配表示扩展到2FE估计量, 以理解这些广泛使用的估计量在非参数框架内的因果解释.更多细节读者可参考Imai and Kim (2020).此外, Imai and Kim (2019)应用他们提出的方法来考虑关于关税和贸易总协定成员资格对二元贸易的因果影响的争议.

另外, 在De Chaisemartin and D'Haultfoeuille (2020)的这篇文章中, 假设在同一$ (g, t) $单元格中的所有观测结果有相同的处置方法, 并且处置方法是二元的, 就像处置方法是以县为单位(county-level law).考虑$ y_{i, g, t} $的回归, 即$ t $期$ g $组单位$ i $在对组固定效应、周期固定效应和$ D_{g, t} $($ t $期$ g $组的处置)的结果.令$ \hat\beta_{\rm fe} $表示$ y_{i, g, t} $在对组固定效应、周期固定效应和$ D_{g, t} $上的最小二乘法(OLS)回归中$ D_{g, t} $的系数.在共同趋势假设下, De Chaisemartin and D'Haultfoeuille (2020)表明$ \beta_{\rm fe} $等于每个处置过的$ (g, t) $单元格中处置效应的加权总和

$ \beta_{\rm fe} = E\left(\sum\limits_{(g, t):D_{g, t} = 1} W_{g, t}\Delta_{g, t}\right), $

其中$ \Delta_{g, t} $为$ g $组和$ t $期的平均处置效应(ATE)并且权重$ W_{g, t} $相加等于$ 1 $但可能是负的.正如De Chaisemartin and D'Haultfoeuille (2020)所阐述的那样, 负权重的产生是因为$ \beta_{\rm fe} $是几个DiD的加权和, 这些DiD比较了各组在连续时间段内结果的演变.然而, 一些比较中的对照组可能在两个时期都进行处置.然后, 它在第二个时期的处置效应被DiD所差分, 因此为负权重.由于负权重, 例如线性回归系数可能是负的, 而所有的ATE都是真正正的.因此, De Chaisemartin and D'Haultfoeuille (2020)提出了另一个估计方法来解决这一问题; 例如, De Chaisemartin and D'Haultfoeuille (2020)中的定理1详细介绍了$ \beta_{\rm fe} $的显式表达式.最后, De Chaisemartin and D'Haultfoeuille (2020)将他们提出的方法应用于两个实际应用:使用面板数据并控制工人的固定影响, 研究了1868年至1928年美国总统选举中报纸对选民投票率的影响, 以及工会成员对工资的影响.

最后, Sun and Abraham (2020)提出了一种替代方法来估计随时间变化的动态效应, 而不是包括处置的超前和滞后的双向固定效应回归, 并且当平行趋势假设只有在观测到的协变量的条件下才可能成立时, 而Callaway and Sant'Anna (2020)考虑了识别和估计问题, 并表明在交错DiD设置中识别了一系列因果参数, 即使观测到的特征差异在组间产生了不平行的结果动态变化. Callaway and Sant'Anna (2020)根据识别结果提出了不同的聚类方案, 可用于突出不同维度的处置效应异质性, 总结参与处置的整体效应.关于细节, 读者可以参考上述文章和其中的参考文献. Sun and Abraham (2020)利用他们提出的方法研究了住院治疗的经济后果, 这是美国成年人经济风险的一大来源, 而Callaway and Sant'Anna (2020)通过分析2001年至2007年美国最低工资对青少年就业的影响, 阐述了他们提出的工具的相关性.

在许多使用面板数据或纵向数据的项目评估应用中, 双因素固定效应(2FE)方法通常被使用, 如上两节所述.问题是2FE估计量与经典估计量有什么不同.实际上, 根据上面对两种方法的描述, 人们可能已经看到了它们之间的区别.然而, 即使使用DiD进行估计所需的识别条件比FE更少, 由于前期零处置条件, 使用DiD减少了估计ATE所需的观测次数.当观测量显著减少时, 可以使用DiD方法.然而, 如果观测数量急剧下降, 则需要使用FE估计, 因为FE可能对ATE产生更稳健的估计.关于以上两种方法的更多比较, 读者可以参考Cerulli (2015)的书.最后, 正像Henderson and Sperlich (2021)那样, 把(2)经典DiD方法推广到非参数情况, 是否可以把上述2FE各种方法推广到非参数情景有待我们进一步探讨和研究, 希望年轻学者可以往这个方向去思考.

本节专门介绍HCW方法及其扩展和应用.为此, 对$ 1\le i\le N $和$ 1\le t\le T $ ($ T\to\infty $), $ y_{it}^1 $表示HCW方法在第$ t $期内对第$ i $个单位的应用结果, 而$ y_{it}^0 $表示没有HCW方法在第$ t $期内对第$ i $个单位的应用结果. HCW方法在第$ t $期内对第$ i $个单位的效果定义为

$ \Delta_{it} = y_{it}^1-y_{it}^0. $

由于无法同时观测到$ y_{it}^1 $和$ y_{it}^0 $, 因此观测到的数据具有以下形式:

$ y_{it} = d_{it}y_{it}^1+(1-d_{it})y_{it}^0. $

如果在时间$ t $内第$ i $单元正在处置, 则$ d_{it} = 1 $, 否则$ d_{it} = 0 $. HCW的模型着重于这样一种情况, 即对$ 1<T_1<T $时只有一个单位在时间$ T_1+1 $后接受处置.在不失一般性的前提下, 假定它是第一个单元.换句话说, 对$ j = 2, \cdots, N $和所有的$ t = 1, \cdots, T $, 以及对第一个单元$ y_{1t} $, $ t = 1, \cdots, T_1 $时, $ y_{jt} $没有应用HCW方法; 只有当$ t = T_1+1, \cdots, T $时, $ y_{1t} $应用了HCW方法. HCW使用以下因子模型来激励他们的估计方法

(3) $ \begin{equation} y_{it}^0 = \alpha_i+b_i^\top f_t+u_{it}, \quad i = 1, \cdots, N, \; \; t = 1, \cdots, T, \end{equation} $

其中$ \alpha_i $为第$ i $个个体特定截距, $ b_i $为$ K\times1 $维因子负荷向量, $ f_t $为$ K\times1 $维向量(不可观测)公共因子, $ u_{it} $为弱相依平稳误差项.如果$ T $和$ N $都很大, 可以采用Bai and Ng (2002)的方法估计$ f_t $的公因数.在$ T $和$ N $都不很大的情况下, HCW提出了一种称为控制单元的新方法, 通过使用$ \tilde y_t = (y_{2t}, \cdots, y_{Nt})^\top $来代替$ f_t $预测处置后的反事实结果$ y_{1t}^0 $.

具体来说, 在HCW方法中, 尽管驱动所有横截面单元的一些共同因素对每个横截面单元的影响可能不同, 但可以假设横截面单元之间的相关性是由它们导致的.因此, 根据$ y_{1t} $和$ \{y_{jt}\}_{j = 2}^N $与(3)中的模型的相关性, HCW, Li and Bell (2017)⁴推导出如下回归模型

⁴HCW在Li and Bell (2017)的假设HCW3下推导(4), 该假设被Li and Bell (2017)所抛弃.

(4) $ \begin{equation} y_{1t} = \beta^\top x_t+u_{1t}, \qquad t = 1, \cdots, T_1. \end{equation} $

为估计反事实结果$ y^0_{1t} $, 其中$ x_t = (1, y_{2t}, \cdots, y_{Nt})^\top $, $ \beta = (\beta_{1}, \cdots, \beta_{N})^\top $, 和$ u_{1t} $是一个零均值和有限方差的特殊误差项.用OLS回归法对系数$ \beta $进行估计,

$ \hat\beta = \arg\min\limits_{\beta}\sum\limits_{t = 1}^{T_1}(y_{1t}-\beta^\top x_t)^2. $

通过假设数据结构在处置前后保持不变和其他假设, 如HCW中列出的假设1$ \sim $6, OLS估计$ \hat\beta $是相合的, 可以估计$ t = T_1+1, \cdots, T $时$ y_{1t}^0 $的反事实预测结果如下:

$ \hat y_{1t}^0 = \hat\beta^\top x_t, \qquad t = T_1+1, \cdots, T. $

最后, 对第一个单位的平均处置效果进行估计:

(5) $ \begin{equation} \Delta_1 = E(\Delta_{1t}) = E(y_{1t}^1-y_{1t}^0). \end{equation} $

可以通过将处置后观测到的结果和估计的反事实结果之间的差异取平均值来构建:

(6) $ \begin{equation} \hat\Delta_1 = \frac1{T_2}\sum\limits_{t = T_1+1}^T\left(y_{1t}^1-\hat y_{1t}^0\right), \end{equation} $

其中$ T_2 = T-T_1 $.可以证明, 这在一些假设下, 如HCW的假设1$ \sim $6, 这个估计量是相合的估计.

备注1  我们可以看到, 使用HCW方法的一个进步是避免像Bai and Ng (2002), Pesaran (2006), Bai (2009)中那样估计公共因子$ \{f_t\} $.但是, (4)中的$ x_t $应该允许包含一些协变量$ Z_t $, 它不是控制单元的一部分, 这样在应用中更有吸引力.这个想法有待我们进一步去探讨.

对于(3)中对时间序列$ \{f_t\} $的要求, HCW的假设中$ \{f_t\} $可以是平稳的, 也可以是非平稳的; 从HCW的备注2中可知, 不过, 还有一个假定$ \sum_{t = 1}^T ||f_t||^2/T $收敛于一个常数, 但是, 对于$ f_t $是一个有或没有漂移的单位根过程, 这个假定显然是不满足的.因此, Bai et al. (2014)认为, 如果$ \{f_t\} $是一个有或没有一个漂移的单位根过程, 不需要做任何线性条件均值函数形式的假设下, Bai et al. (2014)在命题2.1中证明了, 他们仍然可以得到类似于HCW的假设6的一个结果.此外, Bai et al. (2014)表明(6)中的$ \hat \Delta_1 $是在一些假设下(见Bai et al. (2014)的假设1$ \sim $6)是(5)中$ \Delta_1 $的相合估计.

另外, Li and Bell (2017)放宽了HCW中的一些分布假设, 如线性条件均值函数形式假设和HCW中的假设6, 并表明HCW的方法确实适用于更广泛的数据生成过程.然后, Li and Bell (2017)导出了$ \hat\Delta_1 $的渐近分布以便于推断.此外, Ouyang and Peng (2015)将HCW模型应用于2008年中国经济刺激方案的研究, 放宽了HCW的线性条件均值假设, 允许使用非参数条件均值函数, 并将HCW模型推广到半参数设置.还有, Carvalho et al. (2018)将HCW的模型扩展到多个处置单元和非线性模型的情况, 而之前的文献只有一个处置单元, 以及应用一个评估巴西反逃税计划对通货膨胀和其他宏观经济变量影响的程序.最后, 通过应用HCW的方法, Chen et al. (2013)研究了引入指数期货交易对中国股票市场现货价格波动率的影响, Ke et al. (2017)评价了高铁项目对中国高铁节点目标城市经济增长的影响.

最近, Fujiki and Hsiao (2015)对HCW的方法进行了进一步扩展, 以理清当观测到的结果受两种处置方法的影响时一种方法对另一种的影响. Fujiki and Hsiao (2015)使用了1995年1月17日发生的Hanshin-Awaji大地震作为研究问题的动机, 提出这个新的方法, 他们的研究发现地震没有持续的影响, 观测到的持续效应是兵库县的结构变化造成的.

当有大量的控制单元($ N $固定但很大)时, 使用所有的控制单元来估计可能不是最好的选择, 因为大量的协变量通常会导致较大的估计方差, 这反过来又会导致较差的样本外预测.为了选择合适的控制单元, HCW建议使用AIC或其变体, 看看是否需要使用所有的横截面单元.此外, Li and Bell (2017), Carvalho et al. (2018)都建议使用LASSO方法选择控制单元; 也就是说,

(7) $ \begin{equation} \hat\beta_{\rm LASSO} = \arg\min\limits_{\beta}\sum\limits_{t = 1}^{T_1}(y_{1t}-\beta^\top x_t)^2+\sum\limits_{j = 1}^{N}\psi_\lambda(\beta_{j}), \end{equation} $

其中$ \psi_\lambda(\cdot) $是惩罚函数, $ \lambda $是一个惩罚参数.至于如何选择惩罚函数, Li and Bell (2017), Carvalho et al. (2018)取$ \psi_\lambda(\cdot) $为绝对值函数, Wu and Liu (2009)采用平滑修剪绝对偏差(SCAD)罚函数.特别地, Carvalho et al. (2018)在Du and Zhang (2015)建议下使用交叉验证准则选择$ \lambda $, 而且为LASSO估计提供了理论论证.正如Li and Bell (2017)中提到的, 为了获得$ \beta $的LASSO估计, 需要选择$ \lambda $的值, 常见的做法包括使用BIC或删一交叉验证(leave-one-out cross validation)或广义交叉验证方法(generalized cross validation)来选择惩罚参数.如果$ N>T_1 $, 这就是超高维变量选择问题, 可以使用所谓的凹凸方法(concave convex procedure)-SCAD算法, 类似于(7)的思想来估计$ \beta $; 详情可见Kim, Choi and Oh (2008).

众所周知, 如果潜在结果的分布不太集中于均值或存在结果的异质性, 平均处置效果可能不符合理想方法的描述效果.要把握一种处置效果的全局效应, 自然要研究处置效果的整体分布.在本节中, 我们的重点是估计面板数据的分位数处置效果.

对于两期面板数据, Callaway et al. (2018)考虑了一个DiD框架, 在该框架中, 样本中的所有个体在$ t $期不接受处置而一小部分接受处置.设$ D_{it} $为一个处置指示器, 如果在周期$ t $内处置单个$ i $, 则值为1, 否则为0.对于每个个体$ i $, 在周期$ s \in \{t-1, t\} $中存在一对潜在结果$ (y_{is}(0), y_{is}(1)) $, 其中$ y_{is} (0) $和$ y_{is}(1) $分别表示周期$ s $中未处置状态和处置状态的潜在结果.每个人都经历过治疗或未治疗的状态, 但不是两者都有, 因此这对潜在的结果是不可观测到的.然后, 假设两周期面板数据由观测值$ \{(y_{i, t-1}, y_{it}, Z_i, D_{it})\}_{i = 1}^n $组成, 结构如下:

$ y_{i, t-1} = y_{i, t-1}(0), \quad\quad y_{i, t} = (1-D_{it})y_{it}(0)+D_{it}y_{it}(0), $

其中$ Z_i $是一个协变量.潜在结果$ y_{i, t-1}(0) $, $ y_{i, t-1}(1) $和$ y_{it}(0) $, $ y_{it}(1) $在横断面上取决于处置状态$ D_{it} $.

为了衡量处置效果, Callaway et al. (2018)考虑在给定$ Z_i = z $的条件分位数下对处置效果(CQTT)的识别和估计, 衡量分位数处置在$ D_{it} = 1 $, 共同历史$ Z_i = z $的情况下对人群中个体的效果.让$ \mathcal{Z} $成为$ Z_i $的未处置和处置组的共同支持.当$ z\in \mathcal{Z} $时在$ \tau \in (0, 1) $处的CQTT定义为:

$ \Delta_z^{\rm CQTT}(\tau) = q_{y_t(1)|Z = z, D_t = 1}(\tau)-q_{y_t(0)|Z = z, D_t = 1}(\tau), $

其中$ q_{y_t(1)|Z = z, D_t = 1}(\tau) $是在给定$ Z_i = z $和$ D_{it} = 1 $的情况下$ y_{it}(1) $的$ \tau $条件分位数, 同时$ q_{y_t(0)|Z = z, D_t = 1}(\tau) $是在给定$ Z_i = z $和$ D_{it} = 1 $的情况下$ y_{it}(0) $的$ \tau $条件分位数.为了定义$ \Delta_z^{\rm CQTT}(\tau) $, 令$ \Delta y_{it}(0) = y_{it}(0)-y_{i, t-1}(0) $, 同时假设$ \Delta y_{it}(0) $独立于$ Z_i $上的条件独立的处置状态$ D_{it} $, 即经典处置效应文献中所谓的条件独立假设; 详见Liu et al. (2020), Tang (2020).关于检验条件独立假设是否成立, 已有一些文献就此提出; 参见Fang, Tang and Cai et al (2020)及其参考文献.此外, 它还需要做出以下假设.

假设Q1   (分布DiD)对所有$ y\in $supp$ (\Delta y_{it}(0)\, |\, Z_i) $和$ z\in\mathcal{Z} $,

$ P(\Delta y_{it}(0)\le y\, |\, Z_i = z, D_{it} = 1) = P(\Delta y_{it}(0)\le y\, |\, Z_i = z, D_{it} = 0). $

也就是说, 在给定$ Z_i = z $和$ D_{it} = 1 $下, $ \Delta y_{it}(0) $的条件发布和在给定$ Z_i = z $和$ D_{it} = 0 $下, $ \Delta y_{it}(0) $的条件发布是完全一样.

假设Q2   (Copula不变性)对每个$ z\in\mathcal{Z} $和所有$ u, v\in [0, 1]\times [0, 1] $,

$ C_{\Delta y_t(0), y_{t-1}(0)\, |Z = z, D_t = 1}(u, v) = C_{\Delta y_t(0), y_{t-1}(0)\, |Z = z, D_t = 0}(u, v). $

也就是说, 在给定$ Z = z $和$ D_t = 1 $下, $ \Delta y_t(0) $和$ y_{t-1}(0) $的条件Copula和在给定$ Z = z $和$ D_t = 0 $下, $ \Delta y_t(0) $和$ y_{t-1}(0) $的条件Copula是完全一样.

在假设Q1和Q2以及其他一些假设下, Callaway et al. (2018)表明, 感兴趣变量的反事实分布可以从未处置个体的观测结果中识别出来.这意味着, 处置组和未处置组在分布意义上必须相似, 不仅是边缘分布, 而且在某些时期的依赖性.因此假设Q1和Q2在识别中发挥关键作用, 如Callaway et al. (2018)所示.此外, Callaway et al. (2018)提供了$ \Delta_z^{\rm CQTT} (\tau) $的估计, 由$ \hat\Delta_z^{\rm CQTT}(\tau) $表示, 并推导了$ \hat\Delta_z^{\rm CQTT} (\tau) $的渐近结果, 以及一个Bootstrap推断.另外, Callaway et al. (2018)利用他们提出的方法估计了提高最低工资对由种族、性别和教育程度定义的子群体收入分配的影响.

更进一步, Callaway and Li (2019)把上述方法推广到至少有三个观察时间点到面板数据情况($ T\ge 3 $).然后通过假设个体在处置或未处置状态下分别具有潜在结果: $ y_{1t} $和$ y_{0t} $, 他们考虑了分位数处置对已处置(QTT)的影响,

$ \Delta^{\rm QTT}(\tau) = q_{y_{1t}|D = 1}(\tau)-q_{y_{0t}|D = 1}(\tau), $

其中$ q_{y_{1t}|D = 1}(\tau) $是在给定$ D = 1 $的情况下$ y_{1t} $的$ \tau $条件分位数, 而$ q_{y_{0t}|D = 1}(\tau) $是在给定$ D = 1 $的情况下$ y_{0t} $的$ \tau $条件分位数.在假设Q1和Q2以及一些附加假设下, Callaway and Li (2019)提供$ \Delta^{\rm QTT}(\tau) $的估计值, 记作$ \hat\Delta^{\rm QTT}(\tau) $, 并推导了$ \hat\Delta^{\rm QTT}(\tau) $的渐近结果.此外, Callaway and Li (2019)利用提出的这个方法估计了提高最低工资对当地劳动力市场失业率分位数的影响, 发现存在显著的异质性.

备注2  对于有限的面板数据, 如何通过使用2FE方法来刻画异质性处置的特征来估计QTE在文献中似乎没有很好地解决.因此, 未来有可能对这一课题进行研究.

不同于Callaway et al. (2018), Callaway and Li (2019), 假设面板数据是带有协变量$ \{Z_t\}_{t = 1}^T $的$ \{y_{it}, 1\le i\le N\}_{t = 1}^T $, 其中$ Z_t\in R^{d_z} $, 而且$ T $可能很大, 比如$ T\to\infty $.所以, 要求面板数据的每个时间序列是严格平稳的.对第一个单元, 只有$ t = T_1+1 $时接受处置, 其余的$ N-1 $个单位作为对照组, 在整个过程中保持不处置.定义$ T_2 = T-T_1 $.为简化表示法, 对于给定的面板数据, $ \{y_{1t}\}_{t = 1}^{T_1} $表示第一个单位且$ \{(y_{it}, Z_t); 2\le i\le N\}_{t = 1}^{T_1} $表示处置前的剩余单位和协变量, 用$ \{X_{1t}\}_{t = 1}^{T_1} $表示.同时, $ \{y_{1t}\}_{t = T_1+1}^T $是第一个单元的信息且$ \{(y_{it}, Z_t); 2\le i\le N\}_{t = T_1+1}^T $为处置后的剩余单位和协变量, 记为$ \{X_{2t}\}_{t = 1}^{T_1} $.这里, $ Z_t $是一个$ d_z\times 1 $的协变量向量, 它不包含在HCW以及与它的相关文献中.设$ \{y_{1t}^0\}_{t = T_1+1}^T $为反事实结果, $ \{y_{1t}^1\}_{t = T_1+1}^T $为观测结果.然后, 通过分析如图 1所示的实例, 为了刻画其异质性和不对称性, Cai et al. (2021)考虑第一个单元的分位数处置效应, 定义为:

$ \Delta_{\tau} = q_{1\tau}^1-q_{1\tau}^0, $

其中$ q_{1\tau}^j $是当$ j = 0 $和$ 1 $和$ \tau\in (0, 1) $时$ F_j(y) = P(y_{1t}^j\le y) $的第$ \tau $分位.为估计分位处置效果$ \Delta_{\tau} $, 分别估计$ q_{1\tau}^1 $和$ q_{1\tau}^0 $即可.由于第一个单元在$ t\ge T_1+1 $处置下的结果是可观测的, 所以很容易计算出$ \{y_{1t}^1\}_{t = T_1+1}^T $的样本分位$ q_{1\tau}^1 $, 记为$ \hat q_{1\tau}^1 $.估计分位数处置效果的困难是由于$ \{y_{1t}^0\}_{t = T_1+1}^T $是不可观测的, 因此不能直接估计$ q_{1\tau}^0 $.为了估计第一个单元的反事实分位数, 类似于HCW的ATE模型, Cai et al. (2021)提出了一种利用条件CDF和无条件CDF之间的关系的新方法.为了估计$ q_{1\tau}^0 $, 根据$ q_{1\tau}^0 $的定义, 我们有如下等式:

$ P(y_{1t}^0 \leq q_{1\tau}^{0}) = E[F_{y_{1t}^0|X_{2t}}(q_{1\tau}^{0}|X_{2t})] = \tau, $

其中$ F_{y_{1t}^0 | X_{2t}}\left(\cdot | \cdot\right) $表示给定$ X_{2t} $下$ y_{1t}^0 $的条件分布函数.所以, 通过矩估计的方法可以得到$ q_{1\tau}^0 $的估计量, 求解以下样本形式的方程:

(8) $ \begin{equation} \frac{1}{T_2}\sum\limits_{t = T_1+1}^T F_{y_{1t}^0|X_{2t}}(\hat q_{1\tau}^0|X_{2t}) = \tau. \end{equation} $

一般来说, 条件CDF $ F_{y_{1t}^0|X_2}(y|x) $是未知的, 因此上述$ q_{1\tau}^0 $的估计是不可行的.为了从观测数据得到$ q_{1\tau}^0 $的可行估计, 首先需要利用可观测数据来估计$ F_{y_{1t}^0|X_{2t}}(y|x) $.为此, 我们需要做出以下假设, 这实际上, 这个假设类似于上文提到的HCW和相关参考文献中施加的均值设置的假设, 以及Callaway et al. 2018)中的分位数设置的假设(见假设Q1和Q2).

假设Q3   (条件CDF不变性) (i)给定$ X_{1t} $下的$ y_{1t}^1 $和给定$ X_{2t} $下的$ y_{1t}^0 $条件CDFs的结构相同; 也就是说, $ F_{y_{1t}^1|X_{1t}}(\cdot | \cdot) = F_{y_{1t}^0|X_{2t}}(\cdot | \cdot)\equiv F(\cdot | \cdot) $, 以及(ii) $ X_{2t} $的支撑是$ X_{1t} $支撑的一个子集.

假设Q3假定处置组和对照组之间存在某种结构不变性, 这确保了给定协变量, 处置组和对照组之间未处置的潜在结果的分布具有可比性.在假设Q3下, 可以通过观测到的对照组数据来估计处置组的反事实条件CDF.这一假设与Rothe (2010)中的非参数结构模型的假设1基本上一致, 同时, 类似于Hsu, Lai and Lieli (2020)中的假设2.3.因此, 可以利用处置前的观测数据估计条件CDF $ F(y|x) $, 得到$ \hat F(y|x) $.为此, 可以使用一种加权的核估计方法, 在Cai and Wang (2008)中称为双核估计.读者可以参考文献Cai and Wang (2008).然后将估计的条件CDF代入(8)中得到:

$ \frac{1}{T_2}\sum\limits_{t = T_1+1}^T \hat F(\hat q_{1\tau}^0|X_{2t}) = \tau. $

解上述方程得到$ q_{1\tau}^0 $的估计量.最后, 第一个单元的分位处置效果的估计由$ \hat\Delta_{\tau} = \hat q_{1\tau}^1-\hat q_{1\tau}^0 $.在一定的条件下, 而且$ \hat F(y\, |\, x) $满足一定的渐近性质, Cai et al. (2021)得到了$ \hat\Delta_{\tau} $的相合性和渐近正态性.

如果有很多控制单元和协变量个数的时候; 即$ X_{2t} $的维数$ d_x = N-1+d_z $较大, 对于估计QTE方法, 维数诅咒导致采用核回归方法估计条件CDF $ F(\cdot | x) $并不理想.为了克服这一问题, 遵循Hall and Yao (2005)的思想, 可以采用指数方法$ \beta^\top x $来估计$ F(\cdot\, |\, \beta^\top x) $.通过这种方式, 从统计角度来看, 该指数避免了所谓的维度诅咒, 因为它允许我们将多元问题简化单元, 其中可以实现上述单变量设置中的非参数方法, 因为$ \beta^\top x $是单变量.另外, 可以直接使用Hall and Yao (2005)提出的估计程序来估计$ \beta $和$ F(\cdot\, |\, \beta^\top x) $.然而, 上述的估算方法在计算方面有些复杂.为了便于计算方便, 另一种方法是通过分位数回归估计条件CDF, 如Koenker and Bassett (1978)所述, 下面将详细描述.令$ q_\tau(x) $为$ F(y\, |\, x) $的第$ \tau $条件分位数, 使$ q_\tau(x) = F^{-1}(\tau | x)\equiv q(\tau, x) $.然后一个简单的计算可以得到条件CDF和条件分位数之间的关系,

(9) $ \begin{equation} F(y | x) = \int_0^1 I(q(u, x)\le y){\rm d}u\approx \varepsilon+\int_\varepsilon^{1-\varepsilon} I(q(u, x)\le y){\rm d}u, \end{equation} $

对于一个很小的常数$ \varepsilon>0 $.通过假设当$ 1\le t\le T_1 $时给定$ X_{1t} $, $ y_{1t} $的第$ \tau $条件分位函数为$ q_\tau(x) = x^\top\beta(\tau) $, 那么, 条件分位估计为$ \hat q_\tau(x) = x^\top\hat\beta(\tau) $, 其中

(10) $ \begin{equation} \hat\beta(\tau) = \hat\beta_\tau = \arg\min\limits_{\beta_\tau}\sum\limits_{t = 1}^{T_1}\rho_\tau(y_{1t}-\beta_\tau^\top X_{1t}). \end{equation} $

且$ \rho_\tau(v) = v[\tau-I(v<0)] $.因此, 根据(9), 估计的条件CDF $ \hat F(y | x) $为:

(11) $ \begin{equation} \hat F(y | x)\approx \varepsilon+\sum\limits_{j = 1}^m \delta_j I(\hat\beta_{\tau_j}^\top x\le y), \end{equation} $

其中对于任意$ \varepsilon\le \tau_0<\cdots<\tau_m\le 1-\varepsilon $, 当$ m\to\infty $时$ \delta_j = \tau_j-\tau_{j-1}\to 0 $, 由(10)可得$ \hat\beta_{\tau_j} $.显然, 在实际应用中, (11)中的最后一个近似可能对$ \{\tau_j\}_{j = 0}^m $的选择很敏感.不过, 上述想法在实际应用中通常使用, 如Chernozhukov, Fernández-Val and Galichon (2010), Chernozhukov, Fernández-Val and Melly (2013).

最后, 不同于Chen et al. (2013)仅考虑ATE, Cai et al. (2021)运用上述所提出方法, 通过估计QTE来确定引入沪深300指数期货交易对中国股市的VIX及其VVIX可能产生的影响.实证结果表明, 引入沪深300指数期货交易对我国股市VIX及其VVIX均有显著的影响.

备注3  需要注意的是, Cai et al. (2021)仅考虑一个处置, 该假设应该扩展到有多种处置的情况, 如Fujiki and Hsiao (2015)估算ATE的情况.这种扩展似乎有助于评估宏观经济政策的有多个处置的效果, 如Liu et al. (2020)和其他应用.此外, 与Callaway et al. (2018)类似, 人们可能会有兴趣考虑(部分)条件分位数处置效应(CQTE), 比如,

$ \Delta_\tau(v) = q_\tau^1(v)-q_\tau^0(v), $

其中$ v $是$ X $的一个部分, 这些扩展将作为未来的研究课题.

如果$ d_x $很大, Cai et al. (2021)建议使用分位数回归加惩罚的方法来估计条件CDF, 类似于Li and Zhu (2008), Wu and Liu (2009).具体来说, 与(7)类似, 在(10)中加入一个惩罚项, 变成如下:

(12) $ \begin{equation} \hat\beta_{\rm LASSO}(\tau) = \arg\min\limits_{\beta_\tau}\sum\limits_{t = 1}^{T_1}\rho_\tau(y_{1t}-\beta_\tau^\top X_{1t})+\sum\limits_{j = 1}^{d_x}\psi_\lambda(\beta_{\tau, j}), \end{equation} $

其中$ \psi_\lambda(\cdot) $是某个罚函数, 如Li and Zhu (2008)中的绝对函数或Wu and Liu (2009)中的SCAD罚函数.此方法优点之一在于计算简单, 可以通过使用由Sherwood and Maidman (2016)创立R语言"rqPen"包或Yi and Huang (2017)的"hreg"包, 轻松计算(12)中的$ \hat\beta_{\rm LASSO}(\tau) $值.然后, 对带有惩罚的条件分布进行近似估计, 对于一个小常数$ \varepsilon>0 $, 应该有如下表达式:

$ \hat F_{\rm LASSO}(y|x) = \varepsilon+\int_\varepsilon^{1-\varepsilon}I(\hat\beta_{\rm LASSO}(\tau)^\top x\le y){\rm d}\tau, $

其中$ \hat\beta_{\rm LASSO}(\tau) $由(12)给出.

备注4   首先, 如果面板数据中时间序列是平稳的和$ \alpha $-混合的, 根据Chernozhukov, Fernández-Val and Galichon (2010)命题5, 可证明(11)式中$ \hat F(y | x) $是相合的而且有渐近正态性, 如下:

$ \sqrt{T_1}\left[\hat F(y | x)-F(y | x)\right]\;\overset{d}\to\; N(0, V(y|x)), $

其中$ V(y|x)>0 $是其渐近方差.同样, 我们也可以遵循Li and Zhu (2008)的一个类似的主要结果来获得在相依数据的情况下, $ \hat F_{\rm LASSO}(y|x) $的渐近性质.因此, 可以得到$ \hat\Delta_\tau $的渐近性质.最后, 使用(12)中所给出的惩罚分位数回归方法的另外一个优点就是, 通过一些简单的扩展, 甚至可以处理超高维度(ultralhigh dimension)的截面和协变量大于时间序列长度($ d_x>T_1 $)的情况; 详情见Wang, Wu and Li (2012), Sherwood and Maidman (2016), 以及Yi and Huang (2017).这个研究问题值得我们去进一步探讨.

在许多应用领域, 特别是计量经济学, 定量评价经济政策或干预措施的效果是经济研究和政策研究的核心问题之一.从我个人的角度来看, 本文对面板数据(包括有限面板和大型面板)的经济政策评估的最新进展进行了选择性回顾.综上所述, 经济政策评价仍然是一个充满活力和挑战性的研究领域, 值得进一步研究.毫无疑问的是, 在不久的将来这一领域将受到极大的关注.例如, 其重要性和挑战性在于考虑其他方法, 如合成控制方法(synthetic control method, SCM)等; 参见Wan, Xie and Hsiao (2018)通过模拟来估算ATE, 以便比较HCW方法和SCM方法, Cai et al. (2021)的估算大型面板数据的QTE等方法.

随着时间的推移, 经济政策本质上是不同的, 因为同一类型的政策冲击在不同的时期或在不同的经济情景下实施, 相关政策制度的规模是不同的.因此, 本文的部分讨论了通过控制其他策略场景来确定一个策略影响的一些潜在方法.当然, 未来关于时变政策影响能否在这种框架下得到解决的研究是非常有趣的, 也会有一些有趣的应用.除了前面提到的一些开放问题(如上文所述), 用于估算面板数据的ATE和QTE的方法不需要倾向评分函数的说明, 以避免可能的错误假设.另一个避免估计倾向值函数的有趣方法是使用模拟方法来估计反事实的结果, 例如陆昌, 刘详和杨晓光(2021)所提出的方法.此外, 这些方法之间的一些比较(理论和实证)是绝对需要的.

最后, 正如Carvalho et al. (2018), Athey (2019), 洪永淼和汪寿阳(2021), 和萧政(2021)所提到的, 计量经济学和统计结合人工智能, 机器学习(ML)和因果推断在一起进行综合研究, 是一个崭新的研究课题, 以及从ML和统计学或者计量经济学的角度提供见解和理论结果的文献, 如何对使用这些工具来估计面板数据的ATE和QTE的提供了一个很好的参考.实际上, 对于监督性学习, 文献上已经有很多方法, 比如, 正则回归(LASSO, 岭回归), 随机森林, 回归树, 支撑向量机器, 人工神经网络, 矩阵填充(matrix completion and factorization), 深度学习(deep learning), 梯度提升(boosting), 以及模型平均(model averaging techniques)等等, 关于经济学和机器学习之间关系的细节, 参见Athey (2018).比如, Wager and Athey (2018)成功地引进所谓因果森林(causal forest), 是由许多因果树(causal trees)来加权而成, 来刻画不同因果树的各种异质性, 而Carvalho et al. (2018)提出了人工反事实方法(ArCo)来解决高维度面板数据问题.进一步, 这个ArCo方法已经被Masini and Medeiros (2019)推广来处理高维度和非平稳(固定时间趋势或者随机趋势)问题, 以便估计反事实结果.不过, 如何把上述提到的机器学习的方法应用到基于面板数据的ATE和QTE估计问题或者统计推断问题, 建立一套崭新的计量经济学/统计学的方法论和理论体系, 看来不是一件简单的事, 需要国内外学者共同努力去解决.而解决这些问题对年轻学者来说的确是一个挑战, 希望国内学计量经济学或者统计学学者在这个领域能够开创出一片新的研究天地, 为国内学者在这个研究领域树立一个里程碑.